Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 13 705 fois.
La trigonométrie est une branche des mathématiques qui étudie les triangles et les cercles. Les fonctions trigonométriques sont utilisées pour décrire les propriétés d’un angle, les relations trigonométriques dans un triangle donné et les tracés d’un cycle périodique. Apprendre les formules de trigonométrie vous aidera à comprendre, visualiser et tracer ces relations et ces cercles. Si en plus des cours en classe vous vous efforcez de travailler tout seul, vous pourrez comprendre plus facilement les concepts de base de la trigonométrie et vous en servir dans votre quotidien.
Étapes
Partie 1
Partie 1 sur 4:Mettre l’accent sur les principes de la trigonométrie
-
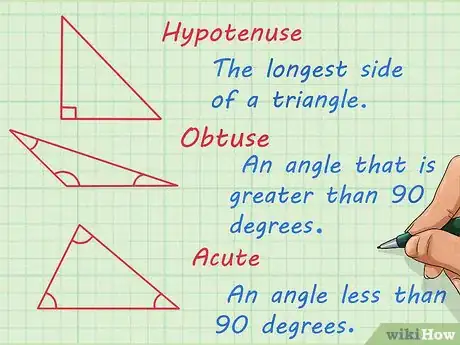
1Identifiez les différentes parties d’un triangle. À la base, la trigonométrie est l’étude des relations entre les longueurs et les angles des triangles. Un triangle a trois côtés et trois angles. Par définition, la somme des angles d’un triangle est de 180 degrés. Vous devez vous familiariser vous-même avec les triangles et certains termes précis pour réussir les problèmes de trigonométrie. Voici quelques-unes des notions les plus utilisées [1] :
- l'hypoténuse, c’est le côté le plus long d’un triangle,
- un angle obtus correspond à un angle supérieur à 90 degrés,
- un angle aigu est un angle inférieur à 90 degrés.
-
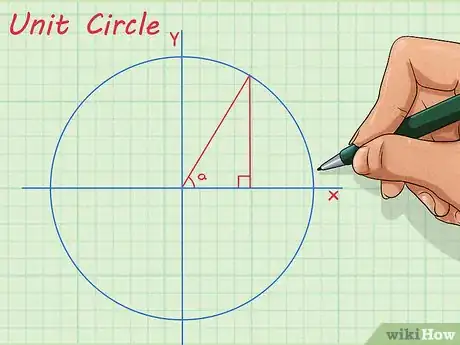
2Apprenez à tracer un cercle trigonométrique. Un cercle trigonométrique vous permet de tracer n’importe quel triangle dont l’hypoténuse vaut « 1 » unité. Cet outil est très utile, car cela a trait aux fonctions trigonométriques, telles que le sinus, le cosinus, etc. Une fois que vous comprenez ce concept, vous pouvez utiliser les valeurs trigonométriques d’un angle donné pour résoudre les problèmes concernant les triangles qui contiennent ces angles [2] .
- Premier exemple : le sinus d’un angle de 30° est égal à 0,5. Cela signifie que le côté opposé à un angle de 30° est égal à la moitié de la longueur de l’hypoténuse.
- Deuxième exemple : cette relation peut être utilisée pour trouver la longueur de l’hypoténuse d’un triangle dont un angle fait 30° et dont le côté opposé à cet angle est de 7 cm. L’hypoténuse devrait être égale à 14 cm.
-
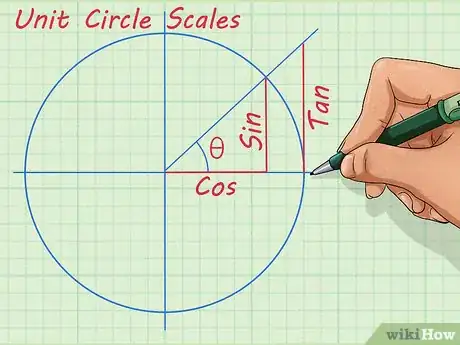
3Essayez de connaitre les fonctions trigonométriques. Il existe six fonctions de base pour comprendre la trigonométrie. Ensemble, elles permettent de définir les relations entre les éléments d’un triangle et de comprendre les caractéristiques particulières de n’importe quel triangle. Voici ces 6 fonctions [3] :
- le sinus (sin)
- le cosinus (cos)
- la tangente (tan)
- la sécante (sec)
- la cosécante (csc)
- la cotangente (cot)
-
4Essayez de concevoir ces relations. Une des choses les plus importantes à comprendre au sujet de la trigonométrie, c’est que les fonctions décrites ci-dessus sont toutes interdépendantes. Bien que les valeurs de sinus, de cosinus, de tangentes et autres aient leurs applications spécifiques, ces fonctions sont extrêmement utiles en raison des relations qui les lient. L’utilisation du cercle trigonométrique vous permettra de retrouver plus facilement ces relations. Une fois que vous comprenez le cercle trigonométrique, vous pouvez exploiter les relations qu’il décrit pour représenter d’autres problèmes [4] .Publicité
Partie 2
Partie 2 sur 4:Comprendre les applications de la trigonométrie
-
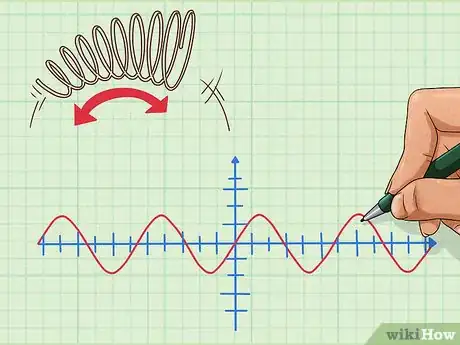
1Comprenez l’utilisation de la trigonométrie dans le milieu universitaire. En plus de pouvoir étudier ce problème mathématique juste pour le plaisir, les mathématiques et les scientifiques appliquent en fait ces concepts à la vie réelle. La trigonométrie vous permet de trouver les valeurs des angles ou des segments linéaires. Vous pouvez également vous en servir pour décrire tous comportements périodiques en les représentant graphiquement comme les fonctions trigonométriques [5] .
- Par exemple, le mouvement d’un ressort qui rebondit peut être décrit graphiquement comme une onde sinusoïdale.
-
2Pensez à des évènements de nature périodique. Parfois, les gens ont du mal à saisir les concepts abstraits en mathématiques ou en science. Si vous vous rendez compte que ces notions sont effectivement présentes dans le monde réel, vous pouvez souvent les voir sous un nouvel angle. Observez des choses qui se produisent de façon cyclique et essayez de les mettre en relation avec la trigonométrie [6] .
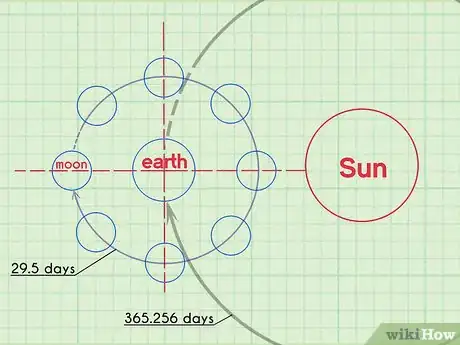
- La lune suit un cycle prévisible qui dure environ 29 jours et demi.
-
3Visualisez l'étude d'évènements cycliques. Lorsque vous vous rendez compte que le monde qui vous entoure regorge de phénomènes cycliques, commencez à penser à la façon dont vous pourriez les étudier avec précision. Songez au graphique qui pourrait représenter ces cycles. À partir de ces tracés, vous pouvez formuler une équation mathématique pour décrire le phénomène que vous étudiez. Cette analyse vous donnera une signification des fonctions trigonométriques pour mieux comprendre leurs utilités [7] .
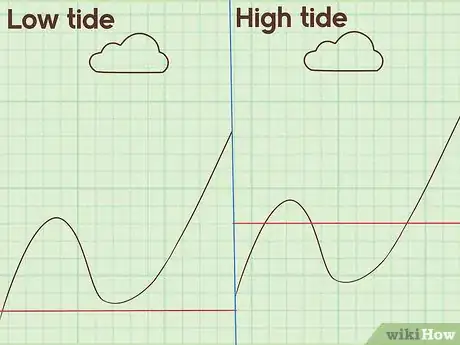
- Essayons de mesurer les vagues sur une plage donnée. Pendant la marée haute, les vagues atteignent une amplitude importante, puis elles se retirent, entrainant ainsi une marée basse. Ce cycle se poursuivra indéfiniment et il peut être représenté sous la forme d’une fonction trigonométrique, telle qu’une onde sinusoïdale.
Publicité
Partie 3
Partie 3 sur 4:Étudier à l’avance
-
1Lisez votre chapitre de trigonométrie. Certaines personnes ont du mal à comprendre les concepts en trigonométrie. Cependant, si vous lisez votre chapitre avant qu’il ne soit traité en classe, vous aurez une plus grande maitrise du contenu du cours. Si vous prenez l’habitude d’étudier de cette manière, vous aurez plus de facilité à établir les liens entre les différents concepts en trigonométrie.
- Ce faisant, vous pourrez identifier les notions qui vous posent problème avant les cours.
-
2Tenez un carnet. Lire vos manuels est mieux que rien, mais la trigonométrie ne s’apprend pas uniquement par cette méthode. Prenez des notes détaillées du chapitre que vous lisez. N’oubliez pas que les cours en trigonométrie sont cumulatifs et les concepts se complètent mutuellement. Alors, le fait d’avoir des notes des premiers chapitres vous aidera à mieux comprendre le contenu des chapitres suivants.
- Notez également toutes les questions que vous souhaitez poser à votre enseignant.
-
3Faites les exercices de votre manuel. Certaines personnes ont une facilité à comprendre les concepts en trigonométrie, mais vous devez faire des exercices. Pour être sûr que vous avez bien assimilé le cours, essayez de résoudre certains problèmes avant la classe. Ainsi, en cas de difficultés, vous saurez exactement de quel genre d’aide vous aurez besoin une fois en classe.
- La plupart des manuelles académiques ont les solutions à certains problèmes à l’arrière. Cela vous permet de vérifier ce que vous avez fait.
-
4Apportez vos documents en classe. Venir en classe avec ses notes et une liste de problèmes mathématiques servira de point de référence. Cela vous permet d’actualiser les informations que vous comprenez et de vous souvenir des concepts qui pourraient nécessiter de plus amples explications. Assurez-vous de clarifier toutes les questions qui figurent dans vos notes.Publicité
Partie 4
Partie 4 sur 4:Prendre des notes en classe
-
1Utilisez toujours le même carnet. Les concepts trigonométriques sont tous liés. Il est préférable que toutes les notes que vous prenez soient au même endroit de sorte que vous puissiez revoir vos premières notes. Choisissez un carnet ou un classeur et utilisez-le uniquement pour les cours de trigonométrie.
- Vous pouvez également résoudre certains exercices dans ce même carnet.
-
2Suivez attentivement les cours. Évitez de profiter de cette occasion pour discuter avec vos camarades ou faire les exercices d’une autre matière. Durant les cours de trigonométrie, il est essentiel de vous concentrer sur la leçon et les exercices faits en classe. Écrivez tout ce qui est au tableau ou toutes les informations jugées importantes.
-
3Restez concentré en classe. Portez-vous volontaire pour résoudre des problèmes au tableau ou partager vos réponses à un exercice en classe. Si vous ne comprenez pas quelque chose, posez des questions. Gardez la communication aussi ouverte que le permet votre professeur. Ce faisant, vous pouvez apprendre plus facilement les concepts et mieux apprécier la leçon.
- Si votre professeur préfère faire son cours sans interruption, vous pouvez garder vos questions et les lui poser après les cours. N’oubliez pas que le rôle de votre professeur est de vous aider à bien comprendre les cours, donc ne soyez pas timide.
-
4Continuez à résoudre d’autres exercices tout seul. Faites vos devoirs de maison, car ils sont d’excellents indicateurs pour avoir une idée des questions qui peuvent être posées lors d’un examen. Si votre professeur ne vous donne pas des exercices à faire à la maison, essayez de résoudre les problèmes de votre manuel et qui ont trait aux concepts abordés dernièrement en classe.Publicité
Conseils
- N’oubliez pas que les mathématiques sont une façon de penser et non pas seulement une série de formules à apprendre.
- Passez en revue les concepts algébriques et géométriques.
Avertissements
- Vous ne pouvez pas apprendre cette matière en vous forçant à la mémoriser. Vous n’avez besoin que de comprendre les concepts liés.
- Étudier à la dernière minute pour un examen est une technique qui fonctionne rarement avec les concepts trigonométriques.
Références
- ↑ http://www.dummies.com/education/math/trigonometry/trigonometry-for-dummies-cheat-sheet/
- ↑ http://www.mathsisfun.com/algebra/trigonometry.html
- ↑ http://www.dummies.com/education/math/trigonometry/trigonometry-for-dummies-cheat-sheet/
- ↑ http://www.mathsisfun.com/algebra/trigonometry.html
- ↑ https://betterexplained.com/articles/intuitive-trigonometry/
- ↑ https://betterexplained.com/articles/intuitive-trigonometry/
- ↑ https://betterexplained.com/articles/intuitive-trigonometry/




























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 13 705 fois.