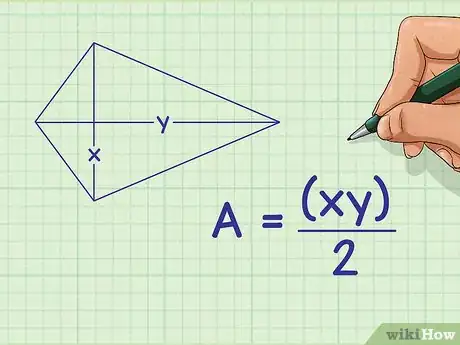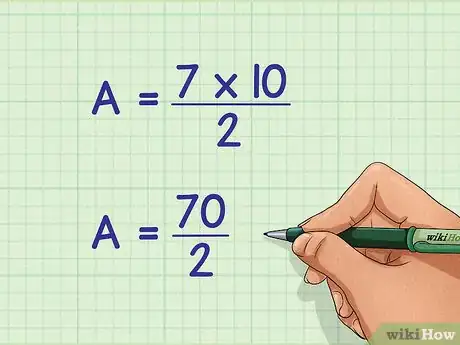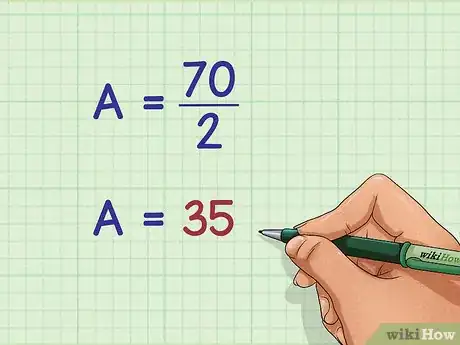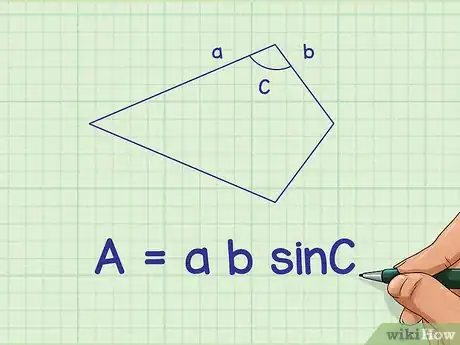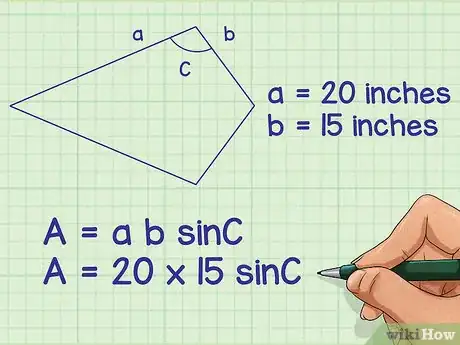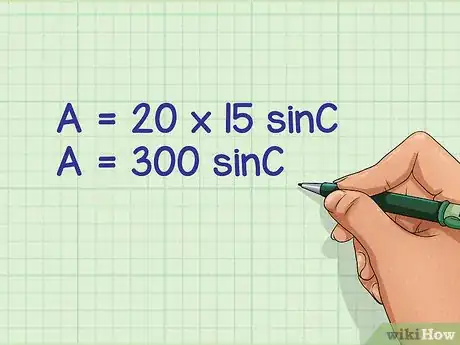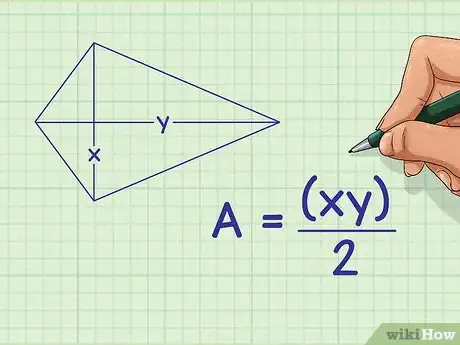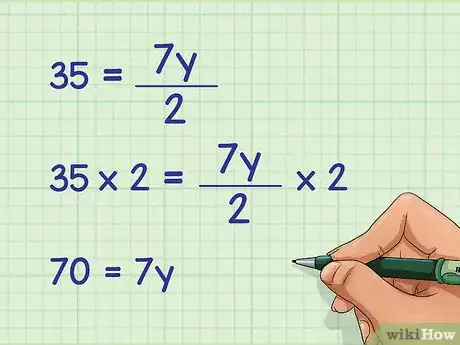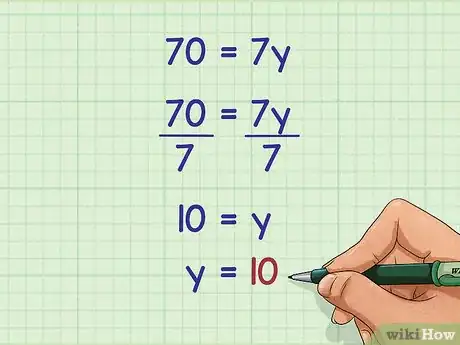Comment calculer l'aire d'un cerf volant

Coécrit par David Jia

Un cerf-volant a généralement une forme de quadrilatère avec deux paires de côtés égaux et adjacents ^{[1]
X
Source de recherche}. Cette forme est la plus souvent utilisée pour les cerfs-volants, mais il en existe qui ont une forme de losange ou même de carré ^{[2]
X
Source de recherche}. Quelle que soit la forme de votre cerf-volant, les formules de calcul de l'aire sont applicables. Pour trouver cette aire, il vous suffit d'avoir, par exemple, les longueurs des deux diagonales ou de deux côtés non congrus et de l'angle correspondant. Dans ce dernier cas, on en passe par la trigonométrie. Rien de très compliqué !

Méthode 1

Méthode 1 sur 3:
Utiliser les diagonales pour calculer l'aire

1
Posez bien la formule de l'aire du cerf-volant. Les deux diagonales sont supposées connues. La formule est la suivante : $A={\frac {xy}{2}}$ , $A$ étant l'aire du cerf-volant, et $x$ et $y$ , les longueurs des deux diagonales du même cerf-volant ^{[3]
X
Source de recherche}.
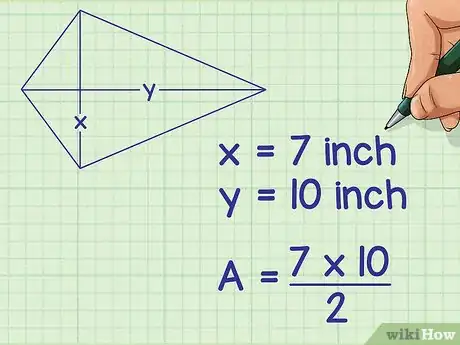
2
Faites l'application numérique. Remplacez $x$ $x$ et $y$ $y$ par leurs valeurs respectives. Une diagonale est un segment qui relie directement deux sommets non consécutifs ^{[4]
X
Source de recherche}. De deux choses l'une : ou on vous donne les longueurs des diagonales ou vous les mesurez vous-même. Bien entendu, s'il vous manque une des deux diagonales, vous ne pouvez pas utiliser cette formule.
- Prenons l'exemple d'un cerf-volant a deux diagonales de 7 cm et 10 cm, la formule de calcul de l'aire (A) sera la suivante : $A={\frac {7\times 10}{2}}$
3
Multipliez les longueurs des diagonales. Ce produit devient le nouveau numérateur dans votre formule.
- Le calcul se présente ainsi :
  $A={\frac {7\times 10}{2}}$
  $A={\frac {70}{2}}$
4
Divisez ce dernier résultat par 2. Vous obtenez alors l'aire de votre cerf-volant en unités carrées.
- Le calcul se présente ainsi :
  $A={\frac {70}{2}}$
  $A=35$
  Pour conclure, l'aire d'un cerf-volant avec deux diagonales de 10 cm et 7 cm, sera de 35 cm².
Publicité

Méthode 2

Méthode 2 sur 3:
Utiliser un angle et deux côtés pour calculer l'aire

1
Posez bien la formule de l'aire du cerf-volant. Il existe une formule pour calculer l'aire d'un quadrilatère quand on connait les longueurs des deux côtés non congrus et la mesure de l'angle entre ces deux côtés. La formule est la suivante : $A=ab\sin({\text{α}})$ $A=ab\sin({\text{α}})$ , $A$ $A$ étant l'aire du cerf-volant, $a$ $a$ et $b$ $b$ , les longueurs des côtés non congrus du cerf-volant, et ${\text{α}}$ ${\text{α}}$ , l'angle intérieur entre les deux côtés $a$ $a$ et $b$ $b$ ^{[5]
X
Source de recherche}.
- Faites très attention à bien prendre deux côtés non congrus. Un cerf-volant a deux paires de côtés congrus. Vous devez prendre un côté de chacune des paires. L'angle qui sert dans la formule doit absolument être celui qui existe entre ces deux côtés. S'il vous manquait l'une quelconque de ces mesures (celles d'un des deux côtés ou celle de l'angle), vous ne pourriez pas utiliser cette formule.
2
Faites l'application numérique. Remplacez $a$ $a$ et $b$ $b$ par leurs valeurs respectives. De deux choses l'une : ou on vous donne les longueurs ou vous les mesurez vous-même. Comme les côtés choisis sont non congrus, leurs longueurs sont, par définition, différentes.
- Prenons l'exemple d'un cerf-volant a un côté de 20 cm et un autre de 15 cm, la formule sera la suivante : $A=20\times 15\sin({\text{α}})$
3
Multipliez les longueurs des deux côtés. Récrivez intégralement la formule avec ce résultat.
- Le calcul se présente ainsi :
  $A=20\times 15\sin({\text{α}})$
  $A=300\sin({\text{α}})$
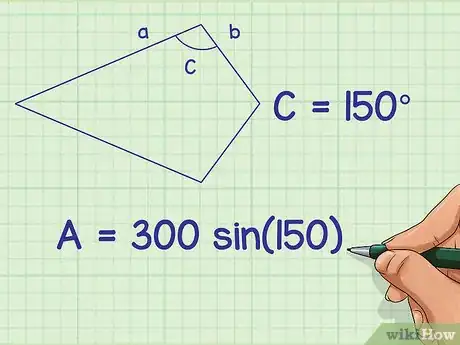
4
Remplacez l'angle par sa valeur en degrés. Vous devez absolument prendre l'angle que forment les deux côtés non congrus, sans quoi votre calcul sera faux.
- Reprenons note exemple et posons que l'angle en question est de $150^{\circ }$ , la formule sera la suivante : $A=300\sin(150)$
5
Calculez le sinus de l'angle en question. Pour cela, vous pouvez utiliser votre calculatrice, une table de trigonométrie ou chercher sur Internet ^{[6]
X
Source de recherche}.
- Dans notre exemple, le sinus de 150° est 0,5. La formule se présente alors de la façon suivante : $A=300(0,5)$
6
Faites le produit. Multipliez le produit des longueurs des côtés par le sinus de l'angle qu'ils forment et vous obtiendrez l'aire du cerf-volant en unités carrées.
- Le calcul se présente ainsi :
  $A=300(0,5)$
  $A=150$
  Pour conclure, l'aire d'un cerf-volant, ayant deux côtés de 20 cm et 15 cm, lesquels forment entre eux un angle de 150°, est de 150 cm².
Publicité

Méthode 3

Méthode 3 sur 3:
Utiliser l'aire pour trouver une des diagonales

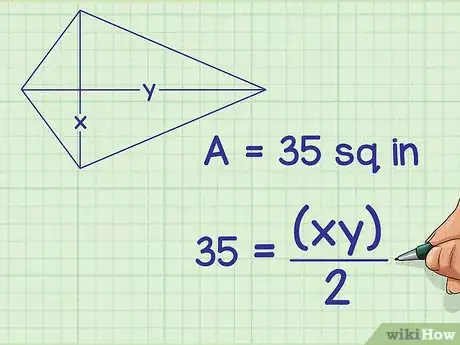
1
Posez bien la formule de l'aire du cerf-volant. Il s'agit de celle qui implique les deux diagonales dudit cerf-volant. La formule est la suivante : $A={\frac {xy}{2}}$ , $A$ étant l'aire du cerf-volant, $x$ et $y$ , les longueurs des diagonales du même cerf-volant ^{[7]
X
Source de recherche}.
2
Faites l'application numérique. Vous devez remplacer $A$ $A$ , l'aire du cerf-volant, par la valeur qui vous aura été fournie par ailleurs.
- Prenons l'exemple d'un cerf-volant a une aire de 35 cm², la formule sera la suivante : $35={\frac {xy}{2}}$
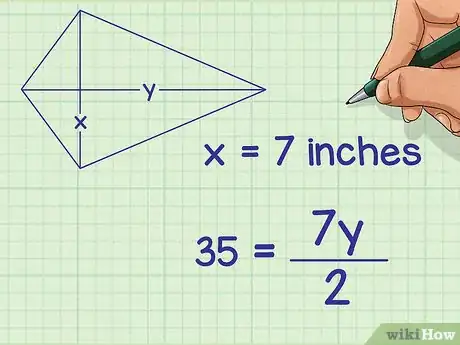
3
Introduisez la longueur de la diagonale connue. Dans la formule, remplacez $x$ $x$ par la longueur qui vous a été fournie.
- Ainsi, si une des diagonales mesure 7 cm de long, la formule sera la suivante : $35={\frac {7y}{2}}$
4
Multipliez de chaque côté par 2. Par cette opération, vous faites disparaitre le dénominateur.
- Le calcul se présente ainsi :
  $35={\frac {7y}{2}}$
  $35\times 2={\frac {7y}{2}}\times 2$
  $70=7y$
5
Simplifiez l'équation. Divisez de chaque côté par la longueur de la diagonale déjà connue. Vous obtiendrez ainsi la longueur de l'autre diagonale.
- Le calcul se présente ainsi :
  $70=7y$
  ${\frac {70}{7}}={\frac {7y}{7}}$
  $y=10$
  Pour conclure, la seconde diagonale d'un cerf-volant de 35 cm², ayant une première diagonale de 7 cm, est de 10 cm.
Publicité