Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 19 774 fois.
Un parallélogramme est une figure géométrique composée de quatre côtés, deux à deux parallèles. Les carrés, les losanges et les rectangles sont des cas particuliers de parallélogrammes, même si la plupart des gens, lorsqu’ils pensent à un parallélogramme, imaginent la figure classique d’un rectangle avec deux côtés plats et deux côtés diagonaux [1] . Indépendamment de l’inclinaison d’un parallélogramme ou de l’angle des sommets, calculer l’aire est une procédure extrêmement simple.
Étapes
Partie 1
Partie 1 sur 2:Trouver l’aire d’un parallélogramme
-
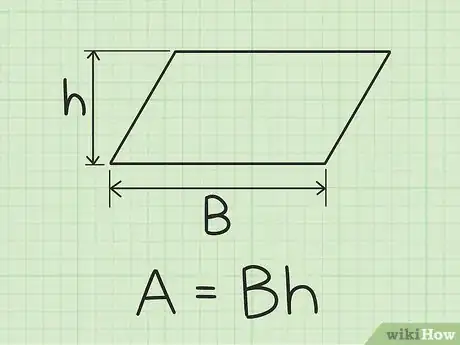
1Multipliez la base par la hauteur. Si le problème de géométrie que vous devez traiter fournit la mesure de la base et de la hauteur de la figure en question, il vous suffira de les multiplier pour obtenir la surface. Supposons que la base de votre figure est de 5 cm et la hauteur de 3 cm, l’aire sera égale à , donc [2] .
- La base d’un parallélogramme correspond au côté le plus long sur lequel repose la figure.
- Alors que la hauteur représente la distance minimale qui sépare les deux côtés les plus longs de la figure.
- C’est à vous de choisir le côté à utiliser comme la base et la hauteur. En fait, vous pouvez pivoter un parallélogramme autant que vous voulez pour le poser sur le côté souhaité, mais le résultat final sera toujours le même [3] .
-
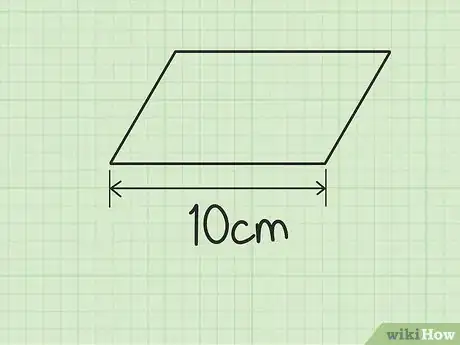
2Mesurez et notez la longueur du côté qui sera la base. Un parallélogramme est composé de deux paires de côtés parallèles l’un à l’autre. Normalement, la figure repose sur l’un des quatre côtés, ce qui donne à la paire de segments en question un aspect parfaitement plat. Mesurez la longueur d’un de ces deux côtés et considérez-la comme la base ou écrivez simplement B.
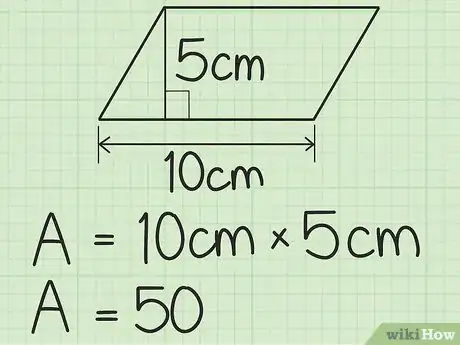
- Par exemple, supposons que la base du parallélogramme étudié soit de 10 cm de long.
-
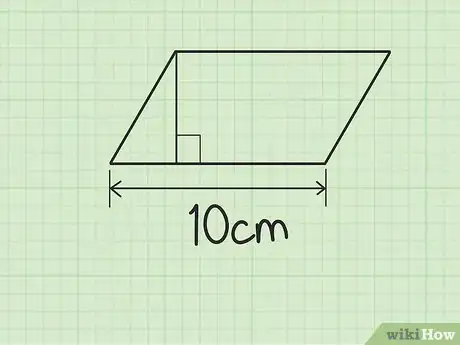
3Tracez une ligne droite de la base jusqu’à son côté parallèle. La ligne en question devra former un angle de 90° avec la base pour que la mesure de la hauteur lui soit perpendiculaire. Le moyen le plus simple d’y parvenir consiste à utiliser une règle et à mesurer la distance minimale, en ligne droite, entre l’un des coins inférieurs de la figure et le côté opposé.
- Il est important de ne pas commettre l’erreur de considérer l’un des côtés obliques comme la hauteur du parallélogramme [4] .
-
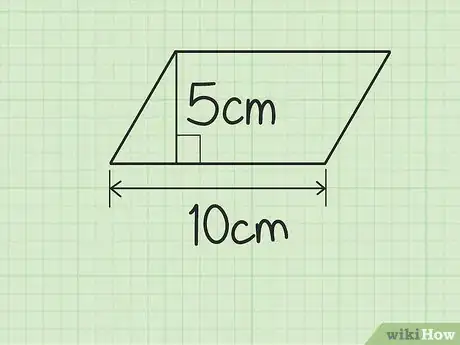
4Trouvez la hauteur. Il vous suffit de mesurer la distance entre la base et le côté opposé. Tant que la ligne que vous mesurez est perpendiculaire à la base de la figure (c’est-à-dire qu’elle forme un angle de 90° avec elle), vous serez sûr d’obtenir la mesure de hauteur. Représentez-la par la lettre H.
- Dans notre exemple, nous supposons que le parallélogramme en question a une hauteur de 5 cm.
- La ligne indiquant la hauteur peut également être dessinée à l’extérieur de la figure.
-
5Multipliez la base par la hauteur pour trouver l’aire. Après avoir obtenu les données nécessaires, entrez-les simplement dans l’équation suivante : , où A est l’aire de la figure. En effectuant les calculs, nous obtiendrons ce qui suit :
-
;
- ;
- ;
- L’aire de notre parallélogramme [5] .
-
;
-
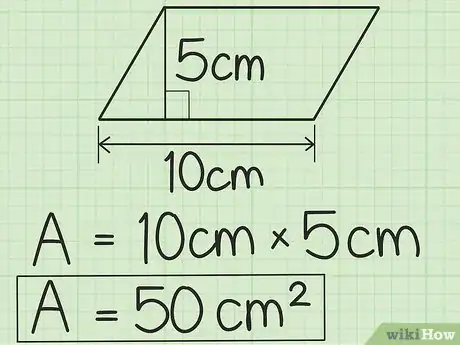
6Sachez que la surface s’exprime en unités carrées. Dans notre exemple, le résultat final est simplement 50. En réalité, cette formulation est incomplète, car elle n’indique pas la dimension réelle de la figure étudiée (en fait, nous ne savons pas s’il s’agit de centimètres, de mètres, de pouces, etc.). Comme l’aire est une mesure de l’espace, il est également nécessaire d’indiquer la taille de cet espace au lecteur, à l’enseignant ou au client. Étant donné que les exemples donnés dans cet article sont exprimés en centimètres, le résultat final doit être exprimé en centimètres carrés. Cela signifie que notre parallélogramme est composé de 5 carrés parfaits d’un centimètre de côté.
- Pour exprimer le résultat final du problème sous sa forme correcte, écrivez le caractère ² en haut de l’unité de mesure avec laquelle les données initiales sont exprimées. Par exemple, si la base et la hauteur sont exprimées en mètres, le résultat final doit être exprimé en mètres carrés ou .
- Si les données initiales ne sont accompagnées d’aucune unité de mesure, le résultat final est suivi du mot unité² [6] .
Publicité
Partie 2
Partie 2 sur 2:Calculer l’aire d’un parallélépipède
-
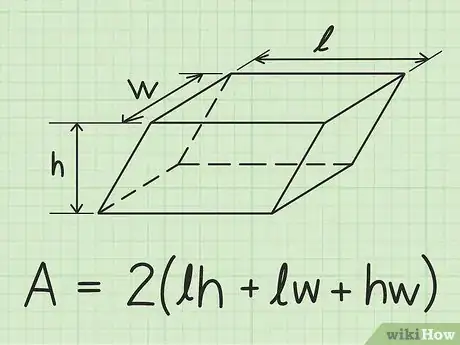
1Procédez comme tout autre problème d’une figure plane. Les parallélépipèdes ne sont rien d’autre que des parallélogrammes en trois dimensions. Le calcul de la surface de ces solides est très simple. Il suffit de connaitre leur longueur (L), leur hauteur (H) et leur largeur (l) et de les insérer dans la formule mathématique suivante :
- Surface latérale = .
-
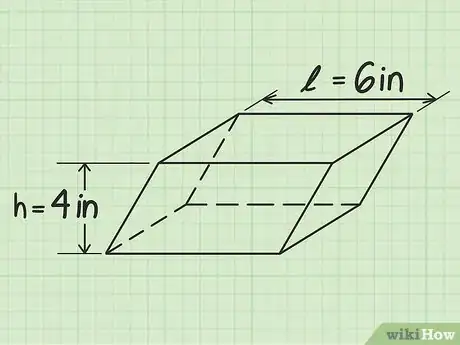
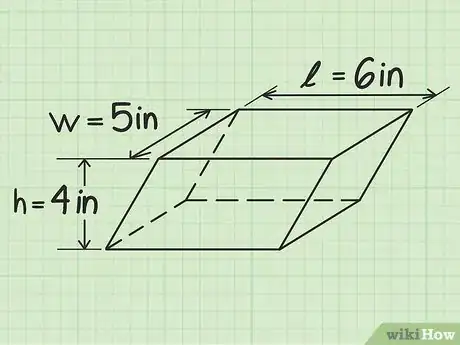
2Identifiez la longueur et la hauteur de l’une des faces. Si vous étudiez un solide rectangulaire (une boite, par exemple), dont l’une des faces correspond à un parallélogramme, vous pouvez mesurer la longueur et la hauteur comme vous mesurez la hauteur et la longueur d’un parallélogramme dans un plan. N’oubliez pas que pour que les mesures soient correctes, les lignes représentant ces deux grandeurs doivent être perpendiculaires, c’est-à-dire qu’elles doivent former un angle de 90°. Ensuite, notez les données obtenues en tant que longueur et hauteur du solide, respectivement [7] .
- Dans le cas d’un parallélogramme, il est bon de se rappeler que la hauteur n’est pas la mesure du côté oblique, mais la distance minimale, en ligne droite, qui sépare le côté identifié comme base du côté opposé et parallèle.
- Dans notre exemple, supposons que nous avons un parallélépipède avec ces dimensions , exprimées en cm.
-
3Trouvez la largeur. Pour cela, mesurez le côté allant dans la direction opposée à celle utilisée comme longueur et hauteur. C’est la dernière dimension que vous n’avez pas encore mesurée. Assurez-vous simplement que vous ne mesurez pas l’un des côtés déjà connus et qu’ils sont parallèles à ceux utilisés pour obtenir la longueur ou la hauteur du solide en question. À partir du même point d’origine (souvent l’un des sommets du parallélépipède), vous devriez pouvoir mesurer les trois grandeurs en question et chaque côté doit être perpendiculaire aux deux autres.
- Dans notre exemple, nous émettons l’hypothèse que le solide en question a une largeur égale à .
-
4Entrez les données mesurées dans la formule de départ. Si les trois grandeurs (longueur, largeur et hauteur) sont déjà fournies dans le problème ou si vous avez réussi à les mesurer, vous pouvez obtenir le résultat final. Entrez les données en votre possession dans la formule suivante :
-
Surface latérale = ;
- ;
- Surface latérale ;
- Surface latérale ;
- Surface latérale ;
- Surface latérale.
-
Surface latérale = ;
-
5Sachez que la surface s’exprime en unités carrées. Dans notre exemple, le résultat final, s’il est simplement indiqué par 148, n’a pas de sens, car nous ne savons pas s’il fait référence à des kilomètres, des centimètres, des mètres, des pouces, etc. L’aire étant évidemment une autre forme de surface, il est nécessaire d’exprimer le résultat en unités au carré, même si vous mesurez des objets ou des figures géométriques tridimensionnelles. Pour notre exemple, les données seront exprimées en centimètres carrés.
- Si, au cours du problème, vous avez oublié quelle unité de mesure utiliser, reportez-vous toujours aux données initiales qui vous ont été fournies ou que vous avez mesurées. N’oubliez pas que cette expression correspond à l’opération mathématique suivante . Pour calculer l’aire d’une surface, il suffit de multiplier les mesures relatives, par exemple . Dans cet exemple, vous pouvez simplement indiquer que la surface est égale à , mais aussi préciser que l’unité de mesure est .[8] .
Publicité
Conseils
Pour tester vos compétences et avoir la preuve de la validité d’un des théorèmes d’Euclide, tracez une diagonale reliant deux angles opposés du parallélogramme, puis tracez deux lignes perpendiculaires entre elles et parallèles aux côtés de la figure géométrique, dont le point d’intersection tombe sur la diagonale. En observant le dessin obtenu, vous remarquerez que deux parallélogrammes ont été formés à l’intérieur du premier, opposés l’un à l’autre et non coupés par la diagonale de ce dernier. La démonstration consiste à montrer que, quel que soit le tracé des lignes perpendiculaires, les deux parallélogrammes obtenus auront toujours la même surface [9] .
Références
- ↑ http://mathworld.wolfram.com/Parallelogram.html
- ↑ http://www.mathopenref.com/parallelogramarea.html
- ↑ http://www.mathgoodies.com/lessons/vol1/area_parallelogram.html
- ↑ http://www.virtualnerd.com/pre-algebra/perimeter-area-volume/perimeter-and-area/area-formulas-examples/parallelogram-area-example
- ↑ http://www.mathopenref.com/parallelogramarea.html
- ↑ http://mathworld.wolfram.com/Parallelogram.html
- ↑ http://mathworld.wolfram.com/Parallelogram.html
- ↑ http://www.mathwords.com/r/rectangular_parallelepiped.htm
- ↑ http://mathworld.wolfram.com/Parallelogram.html
















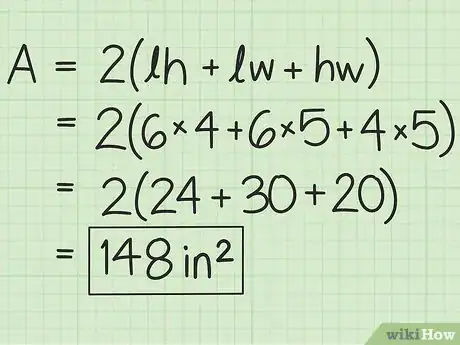






















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 19 774 fois.