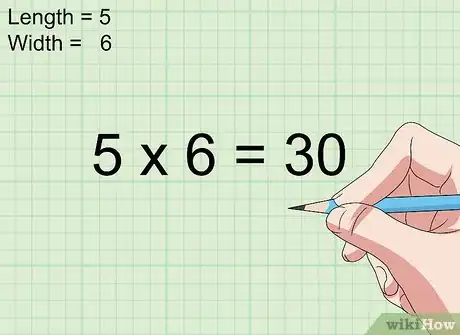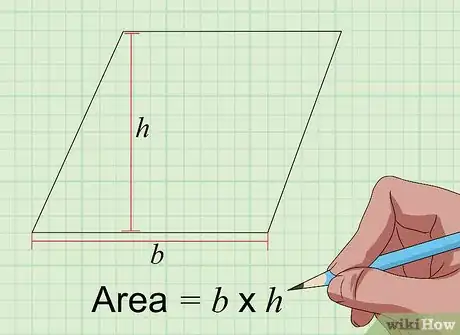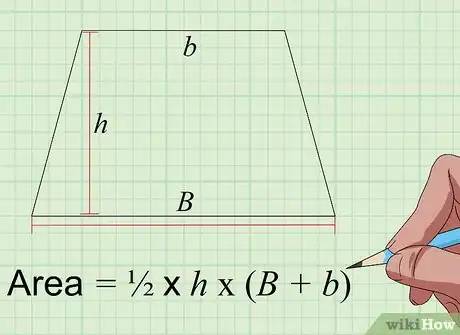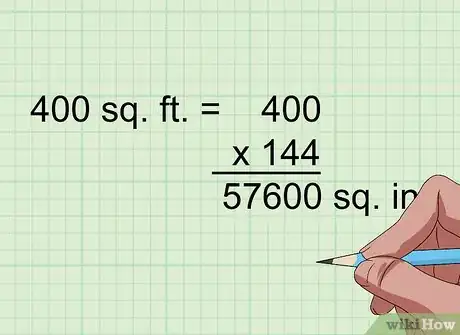Comment calculer l'aire d'une figure géométrique

Coécrit par David Jia

En géométrie, il est souvent nécessaire de calculer l'aire d'une figure. Des formules simples et quasiment intuitives existent pour les figures de base comme le rectangle ou le carré. Elles peuvent cependant devenir plus compliquées pour d'autres configurations. L'unité de mesure de l'aire dépend du système utilisé. En effet, dans le système métrique ou système international, il s'agit du mètre carré, de symbole m². Si vous travaillez avec des mesures anglo-saxonnes, l'unité de mesure de l'aire est le pouce carré ou square inch en anglais et a pour symbole in² ^{[1]
X
Source de recherche}.

Partie 1

Partie 1 sur 3:
Calculer l'aire d'un carré ou d'un rectangle

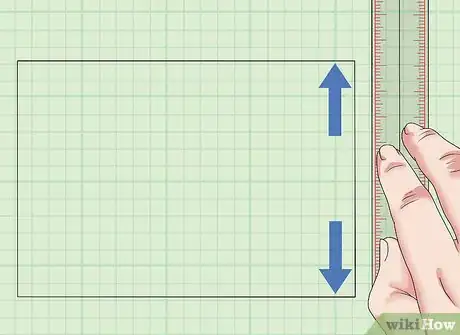
1
Mesurez la longueur du rectangle. Le carré et le rectangle sont des quadrilatères particuliers ^{[2]
X
Source de recherche}. En effet, les côtés d'un rectangle sont égaux deux à deux et il possède au moins trois angles droits. Mesurez son côté le plus long et notez L la valeur trouvée.
2
Mesurez la largeur du rectangle. Notez l la valeur. Pour obtenir l'aire du rectangle, il vous suffit donc de mesurer la longueur de deux côtés adjacents, qui sont deux segments ayant une extrémité commune ^{[3]
X
Source de recherche}.
- Pour le carré, une seule mesure suffit puisque les quatre côtés sont égaux. Autrement dit, la longueur est égale à la largeur.
3
Multipliez la longueur par la largeur. Si l'on reprend les notations précédentes, la surface d'un rectangle vaut L × l.
- Soit un rectangle de 4 cm de longueur et 3 cm de largeur. Son aire vaut donc 4 × 3 soit 12 cm².
- La formule de l'aire pour le rectangle convient également au carré. Compte tenu de ses caractéristiques et si on note c la longueur d'un côté, l'aire d'un carré est donnée par la formule c × c ou plus simplement c². La surface d'un carré de 4 cm de côté vaut donc 4² soit 16 cm².
Publicité

Partie 2

Partie 2 sur 3:
Calculer l'aire d'un cercle ou d'un polygone

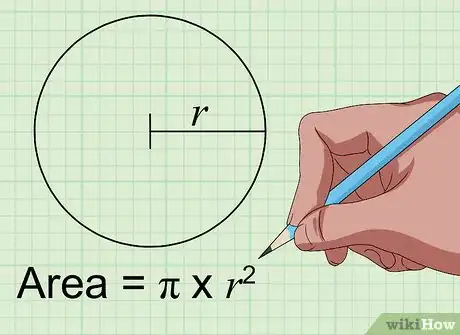
1
Calculez l'aire d'un cercle. La formule est Π × r² ^{[4]
X
Source de recherche}. La variable r est le rayon du cercle, qui est la distance du centre à l'un des points du cercle ^{[5]
X
Source de recherche}. Cette donnée peut vous être fournie dans un énoncé ou mesurée à la règle. Remarquez que la formule fait intervenir la constante mathématique Π (pi) qui vaut environ 3,14.
- Soit un cercle de 4 cm de rayon. Son aire est donc Π × 4², soit Π × 16 = 50,24 cm². Si vous n'avez pas de calculatrice scientifique, arrondissez Π à 3,14.
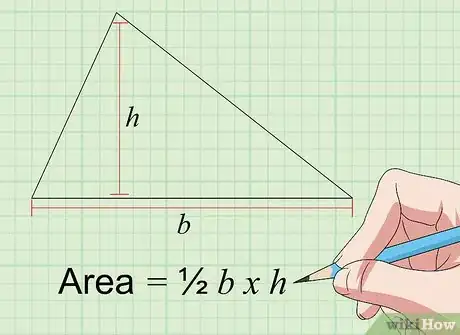
2
Calculez l'aire d'un triangle quelconque. La formule est b × h × 1/2 ^{[6]
X
Source de recherche}. Les variables sont la longueur de la base b et de la hauteur h. La base est l'un des côtés du triangle et la hauteur est la perpendiculaire qui passe par la base et le sommet opposé. Si nécessaire, dessinez la hauteur afin de la mesurer.
- Soit un triangle dont une base mesure 4 cm et la hauteur associée mesure 3 cm. L'aire de la figure est donc 4 × 3 × 1/2 soit 6 cm².
3
Calculez l'aire d'un parallélogramme. Cette figure est un quadrilatère particulier, car ses côtés sont égaux deux à deux. Si elle possède un angle droit, il s'agit alors d'un rectangle ^{[7]
X
Source de recherche}. La formule de calcul de l'aire d'un parallélogramme est b × h, avec b, la longueur d'un côté et h, celle de la hauteur associée. Celle‑ci est la perpendiculaire à un côté passant par le sommet opposé ^{[8]
X
Source de recherche}. Remarquez que pour le rectangle, la hauteur est confondue avec un côté de la figure du fait de l'angle droit.
- Soit un parallélogramme dont la longueur est de 4 cm et la hauteur associée est de 5 cm. Son aire est alors 4 × 5 soit 20 cm².
4
Calculez l'aire d'un trapèze. Un trapèze est un quadrilatère possédant deux côtés parallèles, appelés bases, et deux côtés non parallèles ^{[9]
X
Source de recherche}. Son aire est donnée par la formule (B + b) × h × 1/2 ^{[10]
X
Source de recherche}, avec B, la longueur de la grande base, b, celle de la petite base et h, celle de la hauteur associée. Celle‑ci est le segment perpendiculaire aux deux bases. Notez qu'un trapèze peut être divisé en figures plus simples telles qu'un rectangle et un triangle. Cette décomposition peut vous aider à retrouver son aire.
- Soit un trapèze dont la grande et la petite base mesurent respectivement 6 et 4 cm et la hauteur vaut 5 cm. Son aire est donc 5 × ( 6 + 4 ) × 1/2 soit 25 cm².
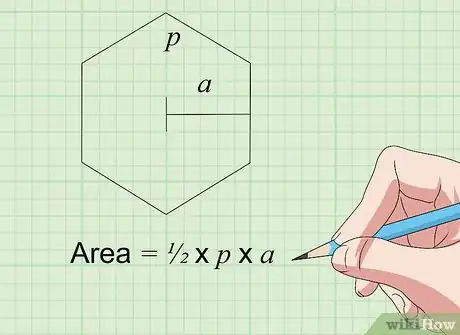
5
Calculez l'aire d'un hexagone régulier. Il s'agit d'un polygone dont les six côtés sont égaux ^{[11]
X
Source de recherche}. Vous pouvez calculer son aire à l'aide de différentes formules, plus ou moins difficiles à retenir. L'une d'elles est P × a × 1/2, avec P, le périmètre de l'hexagone et a, la longueur de l'apothème. Celui‑ci est un segment perpendiculaire à un côté et passant par le centre du polygone. Le périmètre est simplement la somme des longueurs des côtés. Si on note c la longueur d'un côté, le périmètre vaut 6 × c.
- L'hexagone régulier peut se décomposer en six triangles équilatéraux, de côté c. Pour trouver son aire, vous pouvez calculer celle d'un triangle et la multiplier par six. Si on note a, la hauteur d'un triangle, son aire vaut donc c × a × 1/2. En effet, dans un hexagone régulier, l'apothème se confond avec une hauteur d'un triangle qui le compose. L'aire de l'hexagone vaut donc 3 × a × c. Remarquez que l'on retrouve la formule avec le périmètre. Si on remplace P par 6 × c, alors la formule donnée au point précédent donne 6 × c × a × 1/2 soit 3 × a × c. Soit un hexagone de côté 4 cm et dont l'apothème mesure 3,5 cm. Le périmètre vaut 24 cm et l'aire vaut 24 × 3,5 × 0,5 soit 42 cm². En utilisant l'autre formule, l’aire vaut 3 × 3,5 × 4 soit également 42 cm².
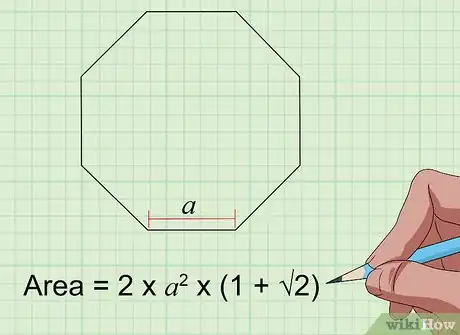
6
Calculez l'aire d'un octogone régulier. Il s'agit d'un polygone dont les huit côtés sont égaux ^{[12]
X
Source de recherche}. Si l'on note c la longueur d'un côté, l'aire de l'octogone est donnée par la formule ^{[13]
X
Source de recherche} 2 × c² × (1 + √2). La seule variable étant la longueur du côté de l'octogone, il vous suffit de le mesurer pour trouver son aire.
- Soit un octogone de 4 cm de côté. L'aire est donc 2 × 4² × (1 + √2) soit 77,25 cm².
Publicité

Partie 3

Partie 3 sur 3:
Travailler avec des unités anglo-saxonnes

1
Familiarisez‑vous avec le système anglo-saxon. L'unité de mesure de l'aire est le pouce carré et celle des longueurs est le pouce ou inch en anglais et de symbole in. Il en existe différents ordres de grandeur. Pour réaliser vos calculs, vous pouvez avoir besoin de convertir les unités anglo-saxonnes entre elles ou de passer du système anglo-saxon au système métrique et inversement ^{[14]
X
Source de recherche}^{[15]
X
Source de recherche}. Les principales équivalences sont :
- 1 in = 2,54 cm
- 1 pied (foot) = 12 in = 30,48 cm
- 1 yard = 36 in = 91,44 cm
- 1 m = 39,3701 in
- 1 cm = 0,3937 in
2
Convertissez des mesures anglo-saxonnes. Comme dans le système international, le système anglo-saxon comporte des déclinaisons des unités de surface. Outre le pouce carré, il existe également le pied carré ou square foot en anglais et de symbole ft². Pour passer d'une unité à l'autre, multipliez la valeur en pieds carrés par 144 pour obtenir son équivalent en pouces carrés.
- Par exemple, une aire de 400 ft² équivaut à 57 600 in².
3
Convertissez des pouces carrés en centimètres carrés. Un pouce valant environ 2,54 cm, un pouce carré équivaut à 2,54² soit 6,45 cm². Pour réaliser votre conversion, vous devez donc multiplier la valeur en pouces carrés par 6,45. Par exemple, on a donc que 250 in² équivaut à 1 612,5 cm² à l'arrondi près.
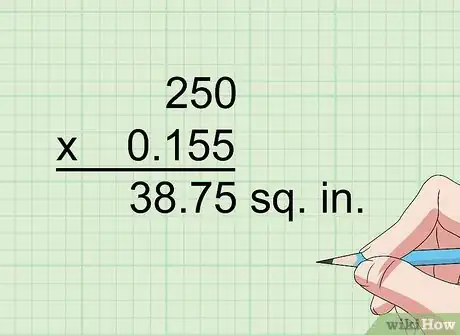
- Pour réaliser la conversion inverse, notez qu'un centimètre vaut 0,394 in. Donc un centimètre carré vaut 0,155 in². Pour obtenir une mesure en pouces carrés, vous devez donc multiplier la valeur en centimètres carrés par 0,155. Si vous travaillez sur des valeurs plus élevées, sachez qu'un mètre carré vaut 10 000 cm² et un kilomètre carré vaut 10¹⁰ cm². Un kilomètre carré équivaut donc à 1 550 003 100 in².
Publicité