Comment calculer l'aire et le périmètre

Coécrit par David Jia

Le périmètre est la longueur totale des côtés extérieurs d'un polygone et l'aire est la surface totale de l'espace qui remplit le polygone ^{[1]
X
Source de recherche}. Ces deux mesures sont extrêmement utiles et peuvent être nécessaires pour de l'aménagement intérieur, de la construction ou du bricolage afin d'estimer la quantité de matériaux qu'il vous faut ^{[2]
X
Source de recherche}. Par exemple, le simple fait de peindre une pièce nécessite de calculer la quantité de peinture dont vous avez besoin basée sur la surface totale que vous allez peindre. Il en va de même pour délimiter des espaces dans un jardin, construire une clôture ou effectuer diverses autres tâches à la maison ^{[3]
X
Source de recherche}. Dans ces situations, vous pouvez calculer diverses aires et les périmètres pour faire des économies de temps et d'argent lorsque vous achetez les matériaux.

Méthode 1

Méthode 1 sur 2:
Calculer un périmètre

1
Identifiez la forme. Déterminez quelle est la forme que vous allez mesurer. Le périmètre est la longueur totale des traits extérieurs constituant une forme géométrique fermée. Il faut employer différentes méthodes en fonction du type de forme. Si elle n'est pas fermée, vous ne pouvez pas calculer son périmètre.
- Si c'est la première fois que vous calculez un périmètre, essayez un rectangle ou un carré. Ces polygones réguliers ont des périmètres très faciles à calculer.
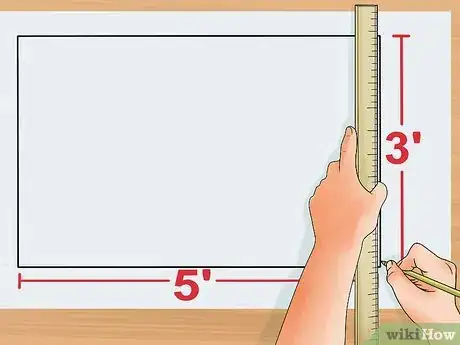
2
Dessinez un rectangle. Tracez-le sur une feuille de papier. Vous vous en servirez pour vous exercer en calculant son périmètre. Assurez-vous que les côtés opposés du rectangle sont de même longueur ^{[4]
X
Source de recherche}.
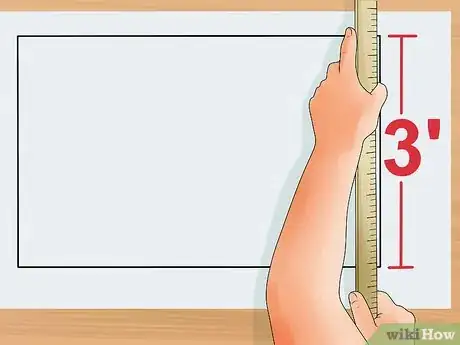
3
Mesurez la largeur. Vous pouvez utiliser une règle graduée ou un mètre ruban ou imaginer un rectangle auquel vous attribuez des mesures. Mesurez un des côtés courts du polygone et écrivez la longueur trouvée à côté pour éviter de l'oublier. Prenons comme exemple un rectangle dont un côté mesure 2 m.
- Pour une petite forme, il est conseillé d'utiliser des centimètres. Pour des périmètres beaucoup plus grands, vous pouvez utiliser des mètres ou même des kilomètres.
- Étant donné que les côtés opposés d'un rectangle sont de même longueur, vous avez seulement besoin d'en mesurer un pour chaque paire ^{[5]
  X
  Source de recherche}.
4
Mesurez la longueur. Mesurez un des côtés longs du rectangle. Vous pouvez vous servir d'une règle graduée ou d'un mètre ruban ou attribuer des mesures à un rectangle que vous imaginez. Écrivez la longueur du côté mesuré à côté de celui-ci.
- Pour notre exemple, imaginons que ce côté a une longueur de 3 m. Le rectangle mesure donc 2 m de largeur et 3 m de longueur.
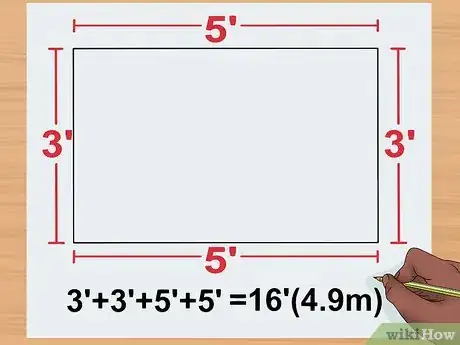
5
Écrivez toutes les mesures. Après avoir mesuré la largeur et la longueur, notez les mesures qui correspondent aux côtés que vous n'avez pas mesurés. Un rectangle a quatre côtés, mais ceux qui sont opposés (c'est-à-dire en face l'un de l'autre) sont de longueur égale, que ce soit dans le sens de la longueur ou de la largeur ^{[6]
X
Source de recherche}. Notez la largeur et la longueur (2 m et 3 m respectivement dans notre exemple) à côté des côtés opposés correspondants.
6
Additionnez les mesures. Sur une feuille de brouillon ou la feuille où vous avez dessiné le rectangle, additionnez les mesures des quatre côtés du polygone ainsi : largeur + largeur + longueur + longueur.
- Dans notre exemple, il faut calculer : 2 + 2 + 3 + 3. Ce rectangle a donc un périmètre de 10 m ^{[7]
  X
  Source de recherche}.
- Étant donné que la longueur et la largeur sont doublées dans cette addition, vous pouvez aussi utiliser cette formule pour calculer le périmètre d'un rectangle : 2(largeur + longueur). Dans notre exemple, cela consiste à multiplier 2 par 2 + 3, c'est-à-dire par 5, ce qui donne un résultat de 10.
7
Adaptez la méthode. Ajustez-la en fonction des formes dont vous mesurez le périmètre. Malheureusement, chaque forme nécessite une formule différente pour calculer son périmètre. S'il s'agit d'un objet réel, vous pouvez utiliser un mètre ruban pour mesurer l'extérieur d'une forme géométrique fermée afin de trouver son périmètre. Vous pouvez également employer les formules ci-dessus pour calculer les périmètres de formes géométriques communes.
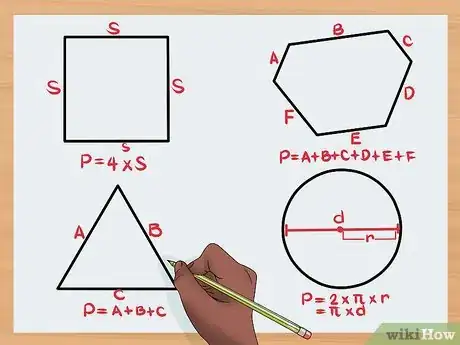
- Carré : longueur de n'importe quel côté x 4
- Triangle : côté 1 + côté 2 + côté 3
- Polygone irrégulier : somme de tous les côtés
- Cercle : 2 x rayon x π OU diamètre x π ^{[8]
  X
  Source de recherche}
  - Le symbole π représente le nombre pi. Si vous l'avez sur votre calculatrice, vous pouvez vous servir de cette touche pour obtenir un résultat aussi précis que possible avec cette formule. Sinon, vous pouvez arrondir la valeur de pi à 3,14 ^{[9]
    X
    Source de recherche}.
  - Le rayon d'un cercle est la distance entre son centre et n'importe quel point sur sa circonférence tandis que son diamètre est la distance entre deux points opposés de son périmètre sur une droite passant par son centre ^{[10]
    X
    Source de recherche}^{[11]
    X
    Source de recherche}.
Publicité

Méthode 2

Méthode 2 sur 2:
Calculer une aire

1
Identifiez la forme. Déterminez ses dimensions extérieures. Tracez un rectangle sur une feuille ou reprenez celui que vous avez déjà dessiné pour calculer le périmètre. Dans notre exemple, vous allez vous servir de la largeur et de la longueur du rectangle pour trouver son aire.
- Vous pouvez utiliser une règle graduée ou un mètre ruban ou attribuer des dimensions à un rectangle que vous imaginez. Dans notre exemple, nous allons utiliser les mêmes dimensions que dans la partie précédente : une largeur de 2 m et une longueur de 3 m.
2
Comprenez ce qu'est l'aire. Lorsque vous cherchez l'aire d'une forme, c'est comme si vous divisiez tout l'espace qui la remplit en petits carrés qui mesurent chacun une unité de largeur et de hauteur. En fonction de la forme, le chiffre correspondant à son aire peut être supérieur ou inférieur à celui représentant son périmètre.
- Si vous voulez visualiser la façon dont cette mesure fonctionne, vous pouvez diviser votre forme en petits carrés en traçant des lignes verticales et horizontales toutes espacées d'une même unité (qui peut être le centimètre, le mètre ou autre chose) sur toute sa surface.
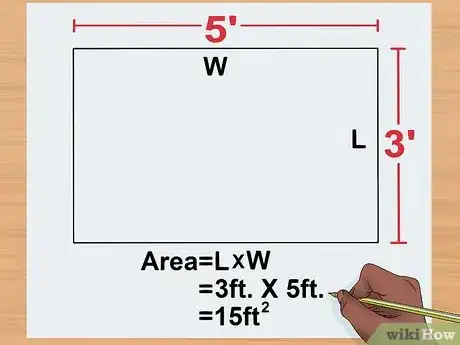
3
Calculez l'aire du rectangle. Multipliez sa largeur par sa longueur. Dans notre exemple, vous devez multiplier 2 par 3, ce qui donne une aire de 6 m². La valeur d'une aire doit toujours être notée en unités carrés (en centimètres carrés, en mètres carrés, etc.).
- Vous pouvez abréger la notation des unités carrées de la façon suivante.
  - Centimètres carrés : cm²
  - Mètres carrés : m²
  - Kilomètres carrés : km²
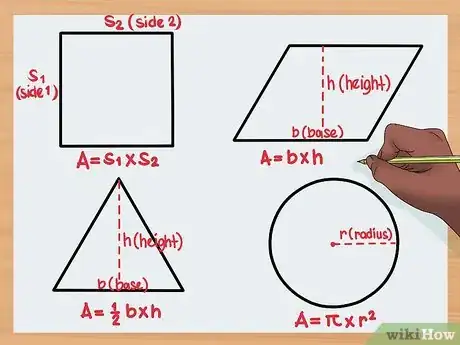
4
Adaptez la méthode. Changez de formule en fonction de la forme dont vous cherchez l'aire. Malheureusement, il faut une approche différente en fonction des différentes formes. Vous pouvez employer les formules ci-dessous pour calculer les aires de formes géométriques communes.
- Parallélogramme : base x hauteur
- Carré : côté x côté
- Triangle : base x hauteur x 0,5
  - Cette formule peut aussi se noter ainsi : ${\frac {bh}{2}}$ .
- Cercle : π x rayon²
  - Le rayon d'un cercle est la distance entre son centre et n'importe quel point sur sa circonférence (ou son périmètre). Le petit 2 qui l'accompagne (qui correspond à la valeur carrée) signifie que le nombre porté au carré doit être multiplié par lui-même ^{[12]
    X
    Source de recherche}^{[13]
    X
    Source de recherche}.
Publicité

Conseils

Ces formules fonctionnent uniquement pour les formes planes (en 2D). Si vous devez mesurer l'espace total qui remplit une forme en 3D (son volume), vous devez chercher les formules de calcul du volume de solides comme des cubes, des cylindres, des cônes, des prismes, des pyramides, etc.