Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 34 248 fois.
Un hexagone est une figure géométrique ayant six côtés d'égale longueur et un apothème, traçable en plusieurs endroits. L'apothème, dont le genre est masculin, est en fait le segment (et par extension, la mesure de ce segment) qui va du centre de l'hexagone au milieu d'un des côtés. C'est une mesure qui est nécessaire, par exemple, au calcul de l'aire de cette figure [1] . Pour déterminer la longueur de l'apothème, vous aurez toujours besoin de connaitre la longueur du côté de l'hexagone.
Étapes
Méthode 1
Méthode 1 sur 2:Calculer l'apothème grâce au théorème de Pythagore
-
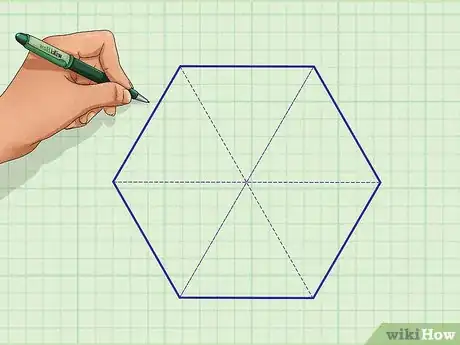
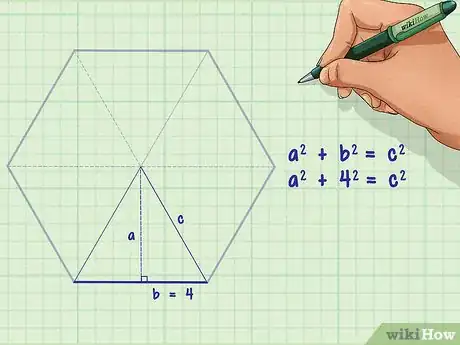
1Divisez votre hexagone en six triangles équilatéraux congruents [2] . Tracez tout simplement les segments qui relient un sommet au sommet opposé, soit trois segments.
-
2Choisissez un des triangles. Prenez celui que vous voulez : vous remarquez que sa base, le côté opposé au sommet, est en fait le côté de l'hexagone.
- Si vous avez un hexagone régulier de 8 cm de côté, alors la base du triangle que vous allez choisir aura une longueur de… 8 cm.
-
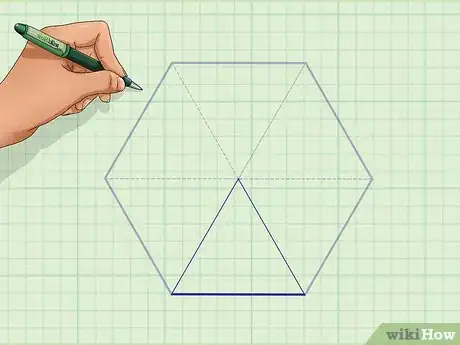
3Partagez votre triangle en deux triangles rectangles. C'est simple, puisqu'il suffit de tracer un trait depuis le sommet vers le milieu de la base. Vous obtenez deux triangles, rectangles sur la base, et la base de chacun d'entre eux est la moitié du triangle de départ.
- Nous étions partis d'un triangle équilatéral de 8 cm de base, les deux triangles rectangles obtenus par division ont chacun une base de 4 cm.
-
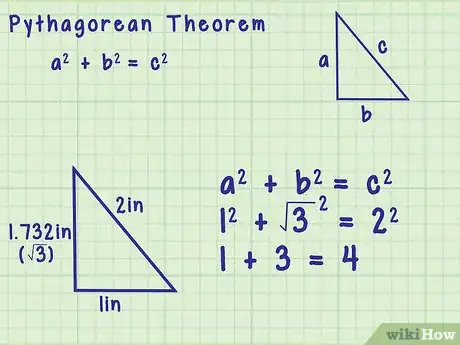
4Inscrivez la formule du théorème de Pythagore. La célèbre formule est la suivante : , étant la longueur de l'hypoténuse (le côté opposé à l'angle droit), et étant les longueurs des deux autres côtés.
- Prenons comme exemple un triangle rectangle ayant deux côtés à angle droit, l'un de 1 cm de long et l'autre, de 1,732 cm, l'hypoténuse mesurant 2 cm. La relation entre ces trois côtés s'établit, conformément au théorème de Pythagore, de la façon suivante : . faites les calculs et vous verrez que l'égalité est vérifiée ().
-
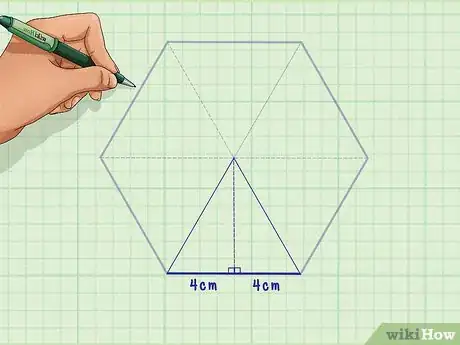
5Faites l'application numérique. Remplacez la base () par la valeur qui vous est donnée ou que vous avez calculée.
- Admettons que cette base mesure 4 cm, la formule devient la suivante : .
-
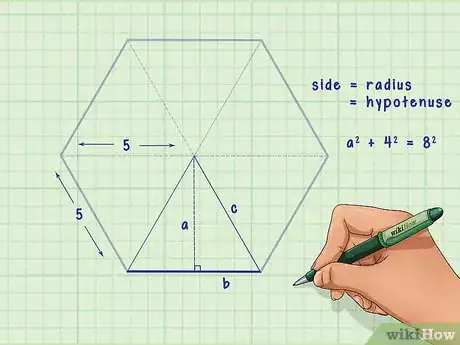
6Poursuivez l'application numérique. Il faut à présent entrer la valeur de l'hypoténuse (), étant entendu que nous cherchons la valeur , celle de l'apothème. Vu que l'hexagone est régulier, cette hypoténuse est égale en longueur au côté de la figure [3] . Cette longueur est en fait le rayon du cercle conscrit à l'hexagone [4] . Comme vous le voyez sur la figure, ce rayon du cercle conscrit est le segment qui relie le centre de l'hexagone à un des sommets.
- Admettons que le côté de l'hexagone est de 8 cm, la longueur de l'hypoténuse du seul triangle rectangle est aussi, par définition, de 8 cm. La formule se présente alors comme suit : .
-
7Élevez toutes les valeurs au carré. Cette opération consiste à multiplier les valeurs en question par elles-mêmes ().
- Une fois les calculs faits, vous devez vous retrouver avec l'égalité suivante : .
-
8Isolez l'inconnue à gauche de l'égalité. Il s'agit tout simplement de la longueur de l'apothème élevée au carré. Pour cette opération, vous devez soustraire de chaque côté la valeur qui correspond à .
- Avec notre exemple, cela donne ce qui suit :
- Avec notre exemple, cela donne ce qui suit :
-
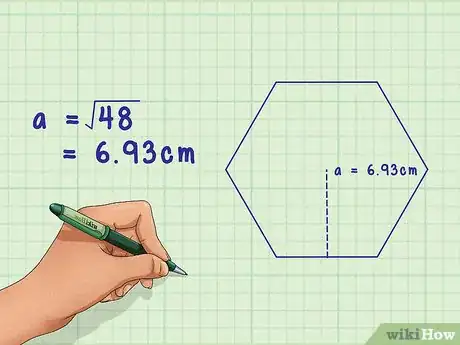
9Trouvez . Pour cela, il vous suffit de calculer la racine carrée des deux membres de l'égalité. Vous obtiendrez alors la valeur de , soit la longueur de l'apothème.
- À l'aide d'une calculatrice, vous trouverez que : . Cette valeur est à la fois la longueur du côté du triangle rectangle, celui qui est perpendiculaire à la base, mais aussi celle de l'apothème de l'hexagone, soit 6,93 cm.
Publicité
Méthode 2
Méthode 2 sur 2:Calculer l'apothème grâce à la trigonométrie
-
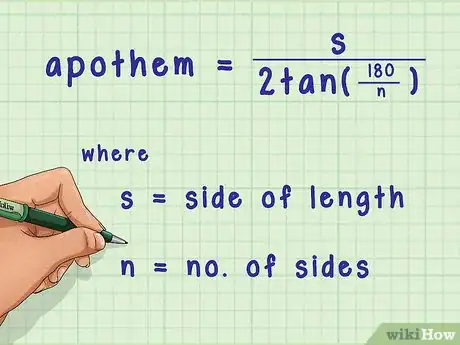
1Utilisez la formule de calcul de l'apothème. La formule se présente comme suit : , étant la longueur du côté du polygone et , le nombre de côtés du même polygone [5] . Elle est valable pour tout polygone régulier
-
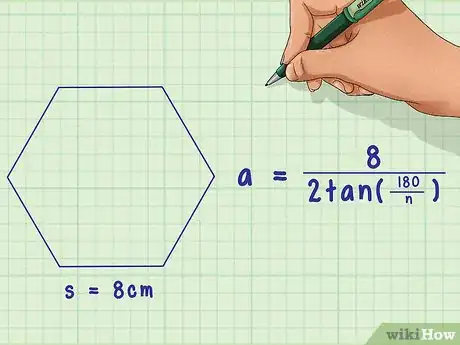
2Commencez l'application numérique. Remplacez la variable par la longueur du côté de votre figure.
- Si l'on vous donnait un hexagone ayant un côté de 8 cm, la formule se présenterait ainsi : .
-
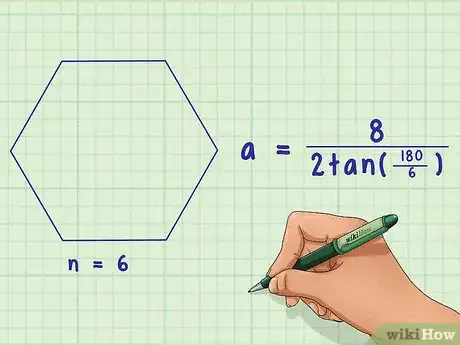
3Poursuivez l'application numérique. Remplacez à présent la variable par sa valeur. L'hexagone étant une figure à 6 côtés, doit être remplacé par 6.
- La formule de calcul est donc la suivante : .
-
4Faites les calculs entre parenthèses. Vous obtiendrez des degrés qui vont servir à calculer le dénominateur en calculant la tangente.
- Le calcul ayant été fait (), vous vous retrouvez avec la formule suivante : .
-
5Calculez la tangente. Pour cela, utilisez soit une calculatrice soit une table trigonométrique (sur papier ou en ligne [6] ).
- Votre calculatrice vous donne comme tangente de 30° un résultat arrondi de 0,577, la formule devient comme suit : .
-
6Multipliez la tangente par 2. Divisez ensuite la longueur du côté par ce résultat et vous obtenez la longueur de votre apothème.
- Les opérations sont les suivantes :
L'apothème d'un hexagone régulier de 8 cm de côté mesure environ 6,93 cm. Fort heureusement pour les mathématiques, nous trouvons exactement le même résultat que dans la première méthode. Selon l'exercice, vous prendrez la première ou la seconde méthode.
Publicité - Les opérations sont les suivantes :
Conseils
- L'apothème n'est pas réservé aux seuls hexagones. Des figures, comme le cône ou la pyramide régulière, ont des apothèmes.
- Ce qui a été expliqué précédemment ne vaut que pour les hexagones réguliers, les irréguliers n'ayant selon toute logique aucun apothème.
Références
- ↑ http://debart.pagesperso-orange.fr/geoplan/polygone_regulier.html
- ↑ https://www.toutcalculer.com/geometrie/surface-hexagone-regulier.php
- ↑ https://fr.wikipedia.org/wiki/Apothème
- ↑ http://www.thedudeminds.net/?p=6650
- ↑ http://www.thedudeminds.net/?p=6650
- ↑ http://www.fguyot.be/MATH/Trigonométrie%20-%20Table%20trigonométrique.pdf








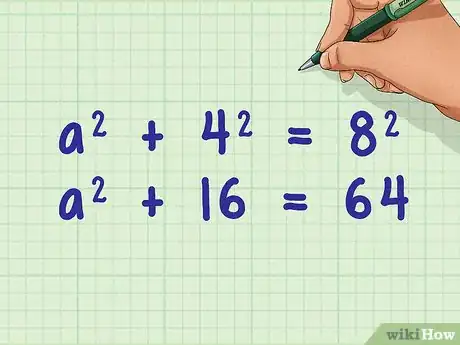











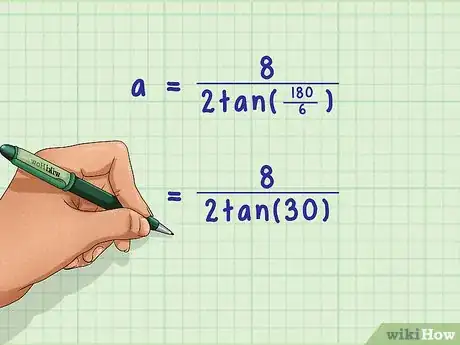


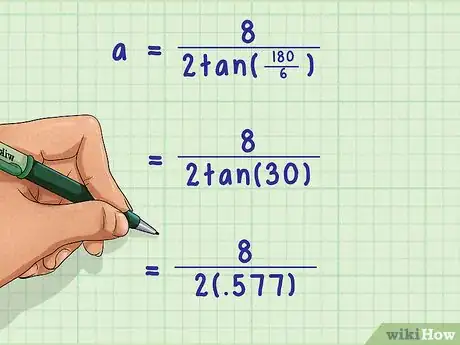
























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 34 248 fois.