Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 43 219 fois.
La méthode la plus connue pour calculer la surface d'un carré est très simple : elle consiste à élever au carré la longueur d'un des quatre côtés. La formule mathématique est la suivante : . Mais parfois, la seule information dont vous disposez est la longueur de la diagonale, qui n’est rien d’autre que la ligne droite qui relie les deux côtés opposés d'un carré. Si vous avez déjà étudié les triangles rectangles, vous pouvez apprendre à calculer la surface d'un carré en ne connaissant que la longueur de sa diagonale.
Étapes
Partie 1
Partie 1 sur 2:Calculer l’aire d’un carré à partir de la diagonale
-
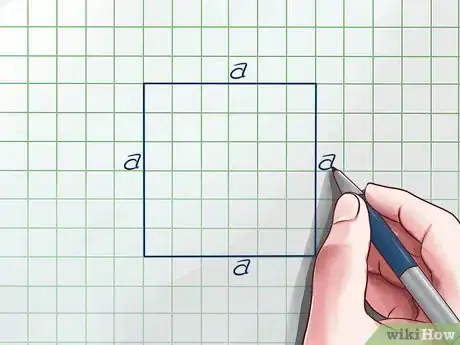
1Dessinez un carré. La caractéristique de cette figure géométrique c’est qu’elle possède quatre côtés parfaitement égaux. Supposons que chaque côté est de la même longueur égale à s.
-
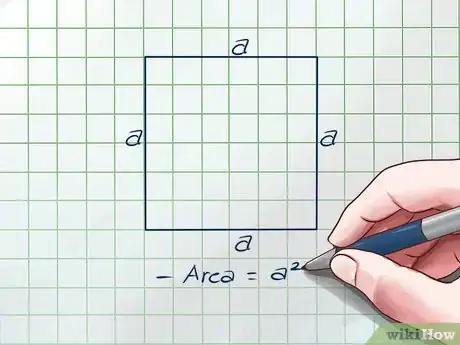
2Essayez de revoir la formule classique de l’aire d’un carré. L’aire de tout parallélogramme est égale à sa longueur multipliée par sa largeur. Dans ce cas particulier, chaque côté a la même longueur s, donc la formule peut être écrite comme ceci : Aire = s x s = s2. Cette étape sera très utile plus tard.
-
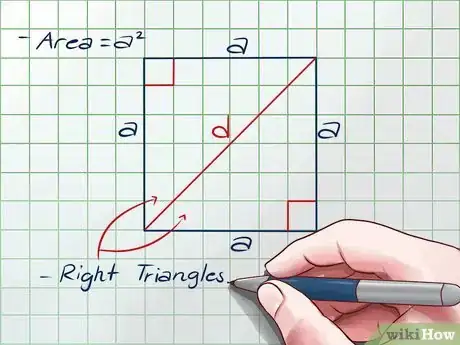
3Reliez deux côtés opposés pour former une diagonale. Supposons que la longueur de la diagonale est égale à d. La diagonale divise le carré en deux triangles rectangles parfaitement identiques.
-
4Appliquez le théorème de Pythagore à l'un de ces triangles. Le théorème de Pythagore est utilisé pour calculer la longueur de l'hypoténuse (le plus long côté) d'un triangle rectangle: (premier coté)2 + (deuxième coté)2 = (hypoténuse)2, ou . Maintenant que le carré a été divisé en deux triangles rectangles, vous pouvez appliquer ce théorème dans l'une des deux figures géométriques.
- Les deux côtés les plus courts du triangle représentent les côtés du carré, et chacun d’eux a la même longueur égale à s.
- L'hypoténuse représente la diagonale du carré et a une longueur égale à d.
- De ce raisonnement, nous déduisons que .
-
5Réécrivez l'équation pour que la variable s2 soit sur un côté. N’oubliez pas : nous savons déjà que l’aire d'un carré est égale à s2. En isolant la variable s2, vous obtenez une nouvelle équation pour calculer l'aire du carré.
- Simplifiez:
- Divisez les deux côtés par deux:
- Aire =
- Aire =
-
6Utilisez la formule obtenue dans un exemple. Les étapes que nous venons d’aborder sont la preuve mathématique que la formule Aire = fonctionne pour tout carré. Remplacez simplement d par sa vraie valeur et résolvez l'équation.
- Par exemple, supposons que la diagonale d’un carré est de 10 cm.
- Aire =
=
= 50 centimètres carrés.
Publicité
Partie 2
Partie 2 sur 2:Tenir compte d’autres informations
-
1Calculez la longueur de la diagonale d'un côté. Le théorème de Pythagore dans un carré de côté égal à s et de diagonale égale à d donnera la formule suivante . Calculez la valeur d si vous connaissez les longueurs des côtés et que vous souhaitez trouver la longueur de la diagonale.
-
- Par exemple, en supposant que les côtés d’un carré mesurent 7 cm, la diagonale sera égal à d= 7√2 centimètres, soit 9,9 cm.
- Si vous ne disposez pas d'une calculatrice, vous pouvez utiliser la valeur approximative de 1,4 comme substitut à √2.
-
-
2Calculez la longueur d'un côté à partir de la diagonale. Si vous avez la valeur de la diagonale et savez que la diagonale d'un carré égal à égale à , il est possible de diviser les deux côtés par pour obtenir .
- Supposons que nous avons un carré dont la diagonale est de 10 cm, la longueur des côtés sera égale à cm.
- Si vous avez besoin de calculer la longueur d’un côté et l’aire d’un carré à partir de la diagonale, il est possible d'utiliser cette formule dans un premier temps, puis d'élever au carré le résultat afin de trouver la valeur de l’aire : Aire centimètres carrés. Ce procédé mathématique est un peu moins précis, étant donné que est un nombre irrationnel pouvant conduire à des erreurs d'arrondissement.
-
3Interprétez la formule de l’aire. La preuve mathématique de la formule de l’aire d'un carré est A = tient la route, mais existe-t-il une autre méthode pour vérifier directement cela ? Bien, représente la surface d’un second carré dont la diagonale est considérée comme un côté. Étant donné que la formule complète est , on en déduit que ce deuxième carré a exactement le double de la surface du carré de départ. Vous pouvez tester ce concept tout seul.
- Dessinez un carré sur une feuille de papier. Assurez-vous que tous les côtés ont la même longueur.
- Mesurez la longueur de la diagonale. Maintenant, tracez un second carré ayant des côtés de longueur égale à ce nombre.
- Faites une copie identique du premier carré pour obtenir 2 autres carrés. Maintenant, découpez tous les trois carrés.
- Découpez les deux petits carrés sous une forme quelconque, de sorte à pouvoir les arranger dans le grand carré. Ils devraient pouvoir remplir parfaitement l'espace disponible, vous prouvant ainsi que l’aire du plus grand carré est exactement égale au double de celle du plus petit carré.
Publicité
Conseils
- Cette équation simple est utilisée dans divers domaines de la vie réelle, par exemple en cristallographie, en chimie et en art. Par exemple, vous pouvez vous en servir pour calculer l’aire d'un terrain au cours d'une étude topographique ou lorsque vous devez utiliser des techniques de perspective géométrique pour photographier un paysage ou peindre quelque chose. Pour ce faire, mesurez simplement la distance parcourue et imaginez une grille avec cette distance comme diagonale.
- Si vous préférez une approche graphique, ou si vous voulez apprendre à utiliser des tableaux et des graphiques dans l'art, parcourez les articles de la Catégorie:Mathématiques ou faites des recherches sur Internet.
- Si vous ne disposez pas d'une calculatrice et avez besoin d’obtenir un résultat très précis de la racine carrée de 2, il y a des façons de le faire à la main. L’une des façons de calculer manuellement la valeur d'un radical consiste à utiliser la méthode de Newton-Raphson [1] .








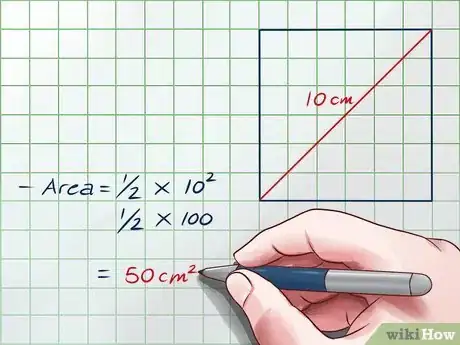





























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 43 219 fois.