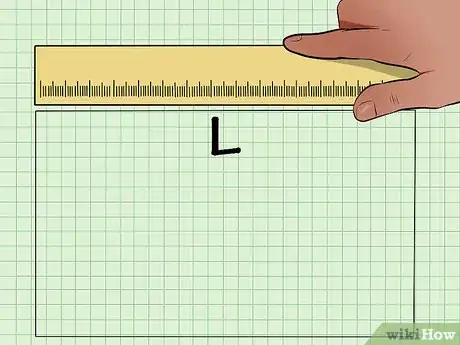Comment calculer l’aire d’un rectangle

Coécrit par David Jia et Hunter Rising

Un rectangle est un quadrilatère dont deux des côtés ont la même longueur et les deux autres côtés ont la même largeur. C’est une figure géométrique à quatre angles droits. Pour trouver l'aire d'un rectangle, tout ce que vous avez à faire est de multiplier sa longueur par sa largeur. Si vous voulez savoir comment trouver l'aire d'un rectangle, il suffit de suivre ces quelques étapes très simples.

Méthode 1

Méthode 1 sur 3:
Comprendre ce qu’est un rectangle

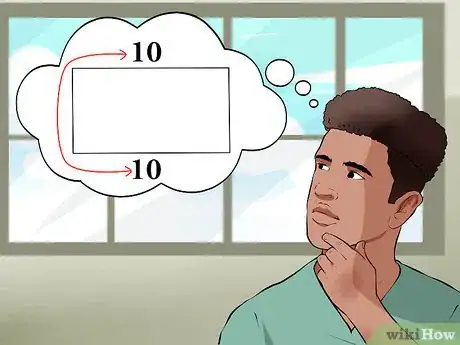
1
Comprenez ce qu’est le rectangle. Le rectangle est un quadrilatère, ce qui signifie qu'il a quatre côtés. Ses côtés opposés sont de même longueur, de sorte que les longueurs sont égales, et les largeurs également. Par exemple, si un côté du rectangle est de 10,alors le côté opposé sera également de 10.
- Cas particulier : chaque carré est un rectangle, mais tous les rectangles ne sont pas des carrés. Aussi, calculez la surface d’un carré comme vous le feriez pour un rectangle.
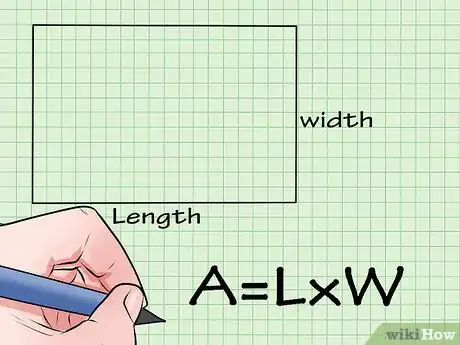
2
Sachez la formule de calcul de l'aire d'un rectangle. La formule de calcul de l'aire d'un rectangle est simple : S = L x l (S est la surface, L est la longueur et l, la largeur). Il suffit donc de multiplier la longueur par la largeur du rectangle.

Publicité

Méthode 2

Méthode 2 sur 3:
Trouver l'aire d'un rectangle

1
Trouvez la longueur du rectangle. Dans la plupart des cas, on vous donnera la longueur, sinon vous pouvez la trouver à l'aide d'une règle.
- Notez que les deux traits sur les côtés du rectangle signifient que les longueurs de ces deux côtés sont identiques.
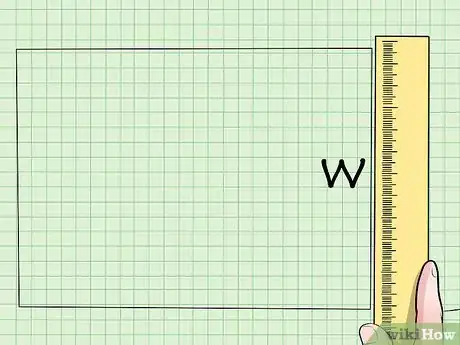
2
Trouvez la largeur du rectangle. Dans la plupart des cas, on vous donnera la largeur, sinon vous pouvez la trouver à l'aide d'une règle.
- Notez qu’un simple trait sur les côtés du rectangle signifie que les deux largeurs sont identiques.
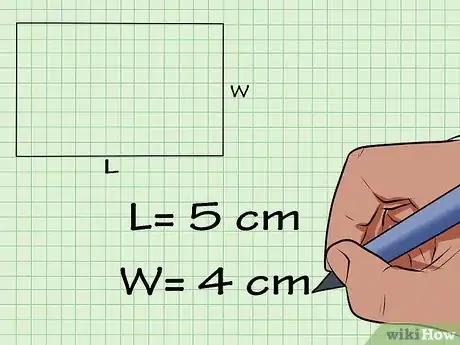
3
Inscrivez la longueur et la largeur l’une en dessous de l'autre. Dans cet exemple, la longueur est de 5 cm et la largeur, de 4 cm
4
Multipliez la longueur par la largeur. Faites l’application numérique avec la formule S = L x l pour trouver la surface.
- S = 4 cm x 5 cm
- S = 20 cm²
5
Indiquez votre réponse en unités carrées. Votre réponse finale est de 20 cm², ce qui donne "vingt centimètres carrés".
- Vous pouvez écrire votre réponse finale de deux façons, soit 20 cm carrés, soit 20 cm².
Publicité

Méthode 3

Méthode 3 sur 3:
Trouver la surface en ne connaissant qu’un seul côté et la diagonale

1
Utilisez le théorème de Pythagore. Le théorème de Pythagore est une formule pour trouver le troisième côté d'un triangle rectangle en connaissant la valeur de deux des côtés. Vous pouvez l'utiliser pour trouver l'hypoténuse d'un triangle, qui est son côté le plus long, ou sa longueur ou largeur, qui se croisent à un angle droit.
- Comme un rectangle est composé de quatre angles droits, la diagonale sépare deux triangles rectangles, de sorte que vous pouvez appliquer le théorème de Pythagore.
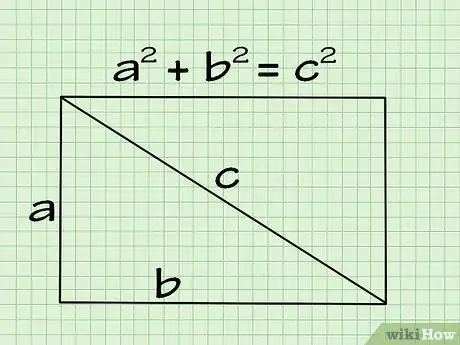
- Le théorème repose sur l’équation suivante : a ² + b ² = c ², où a et b sont les deux côtés adjacents du triangle et c, l'hypoténuse (côté le plus long)
2
Utilisez le théorème de Pythagore pour trouver l'autre côté du triangle. Soit un rectangle avec un côté de 6 cm et une diagonale de 10 cm. Vous avez donc 6 cm pour un côté, b sera l'autre côté, et 10 cm sera votre hypoténuse. Maintenant il suffit de faire l’application numérique à partir de l’équation du théorème de Pythagore. Voici comment procéder.
- Exemple : 6 ² + b ² = 10 ²
- 36 + b ² = 100
- b ² = 100 - 36
- b ² = 64
- √b ² = √64
- soit b = 8
  - La longueur de l'autre côté du triangle, et de son côté opposé, est donc de 8 cm.
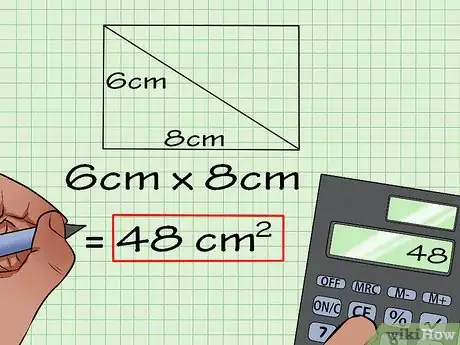
3
Multipliez alors la longueur par la largeur. Grâce au théorème de Pythagore, vous avez trouvé la longueur et la largeur du rectangle : tout ce qu’il reste à faire est de les multiplier.
- Exemple : 6 cm x 8 cm = 48 cm²
4
Indiquez votre réponse en unités carrées. Votre réponse finale est de 48 cm², ou encore 48 centimètres carrés

Publicité

Conseils

Tous les carrés sont des rectangles. Cependant, tous les rectangles ne sont pas des carrés.
Si vous calculez une surface, votre réponse sera toujours en unités carrées.