Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 7 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 7 555 fois.
La résultante est la force correspondant à la somme vectorielle de tous les vecteurs forces qui s’appliquent à un corps. Un objet sur lequel s'applique une résultante nulle est à l'équilibre. Par contre, si elle est n'est pas nulle, l'objet serait sujet à une accélération [1] . Pour calculer cette résultante, vous devez connaitre pour chaque force qui s'exerce sur un objet sa direction, son sens et son intensité. Tout exercice qui vise à déterminer la force résultante nécessite de faire un croquis sur lequel toutes les forces seront correctement placées et identifiées.
Étapes
Partie 1
Partie 1 sur 2:Déterminer une force résultante
-
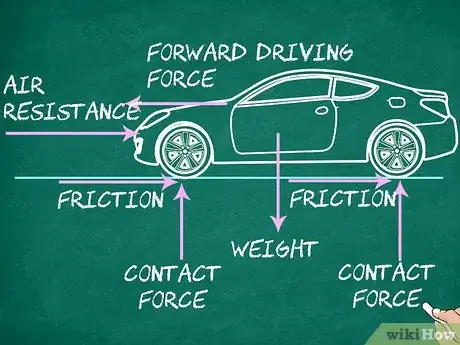
1Tracez un croquis simplifié. Un dessin vaut mieux qu’un grand discours : cet adage est vrai quand il s’agit de trouver la force résultante agissant sur un objet physique (voiture, boule, vélo, etc.). Lisez attentivement le problème, identifiez les forces en action et tracez-les sur un croquis [2] .
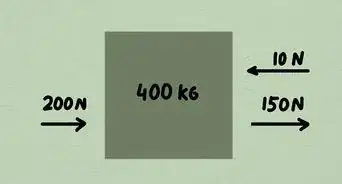
- Résolvons le problème suivant : « calculez la résultante d’un objet à l’arrêt, posé sur un plan horizontal pesant 20 N et à qui l’on appliquerait une force de 5 N depuis la gauche, les forces de frottement étant estimées à 5 N. »
-
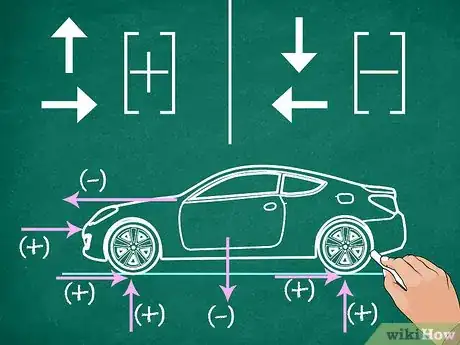
2Repérez et indiquez le sens des forces. Par convention, sont de signe positif toutes les forces ayant un sens vers le haut et la droite, négatif vers le bas et la gauche. Sur un objet, plusieurs forces peuvent s’exercer dans un même sens. Deux forces allant dans des sens opposés ont des intensités de signe opposé, l’une est négative, l’autre positive [3] .
- Sur votre croquis, vous ferez toujours très attention au sens des forces qui s’exercent : là est souvent le piège !
- Sur ce même croquis, vous pouvez accoler à l’intensité un ou un , selon que la force va dans tel ou tel sens. C’est le vecteur force qui vous donnera le signe.
- À titre d’exemple, la gravité est une force qui attire les objets vers le bas, c’est une force négative. Un objet posé sur le sol déclenche une réaction, vers le haut, c’est une force positive. Si une force va vers la droite, ce serait une force positive, mais une force de frottement va alors vers la gauche, donc négative.
-
3Identifiez clairement toutes les forces. N’en oubliez aucune ! Quand un objet repose sur le sol ou une table, son poids () exerce une force vers le bas. Ce même objet reçoit du sol une force opposée, mais de norme identique : c’est la réaction normale (). D’autres forces peuvent s’appliquer sur un objet, votre schéma doit les indiquer toutes (directions, sens et intensités [4] ).
- Une force s’exprime par la lettre suivie d’un indice précisant la nature de la force. C’est ainsi que la force de friction est notée .
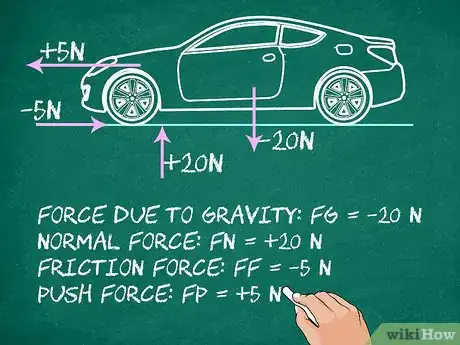
- À titre d’exemple, supposons un objet de poids () dû à la gravité :
- Supposons une réaction normale du plan : .
- Supposons une force de frottement : .
- Supposons enfin une force appliquée : .
-
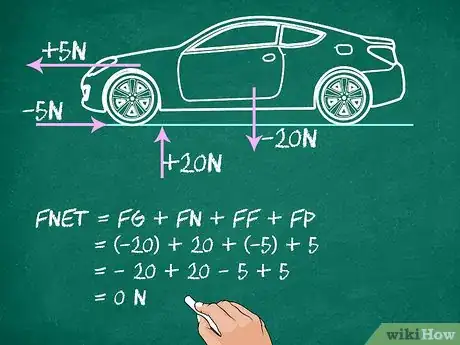
4Faites la somme des intensités de toutes les forces. Voilà ! Sur votre croquis, vous avez toutes vos forces. Pour trouver la résultante (), laquelle va vous permettre de connaitre le mouvement de l’objet, faites la somme des intensités de toutes ces forces en n’oubliant pas les signes [5] .
- Dans notre exemple, cela donne :
. Cette résultante étant nulle, votre objet est à l’équilibre.
Publicité - Dans notre exemple, cela donne :
Partie 2
Partie 2 sur 2:Trouver une force résultante sur un plan incliné
-
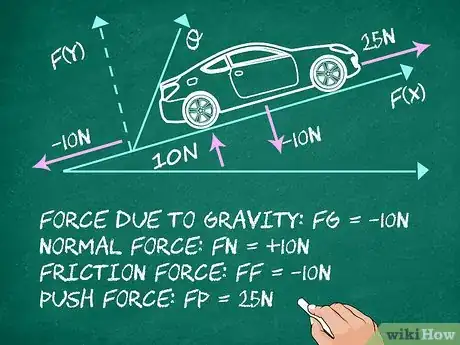
1Faites un croquis des forces. Il est encore plus utile que pour un objet sur un plan. Sur une pente, une force () appliquée avec un angle (noté ) doit être décomposée (par projection) en deux forces par rapport à un repère (, ) : et . L’angle est mesuré à partir du plan de l’objet dans le sens contraire des aiguilles d’une montre [6] .
- Tracez votre objet (voiture sur un plan incliné). Indiquez l’angle de la force de traction, vers le haut et la droite.
- Dessinez toutes les autres forces qui agissent sur l’objet et indiquez leurs intensités.
- Prenons l’exercice suivant : « dessinez le croquis d’une voiture miniature de 10 N subissant une poussée de 25 N vers le haut et la droite à un angle de 45°. La force de frottement vers la gauche est de 10 N. »
- Les forces en jeu sont les suivantes :
.
-
2Calculez les composantes de la force de traction . Le repère sera parallèle et perpendiculaire à la pente. Chacune d’entre elles, avec la force principale, forme un triangle rectangle. Grâce à la trigonométrie, il est facile de calculer les intensités des composantes : la force est l’hypoténuse et et sont les côtés adjacent et opposé [7] .
- Pour mémoire, la formule du cosinus est :
. Pour notre exemple, nous avons :
. - Pour mémoire, la formule du sinus est :
. Pour notre exemple, nous avons :
. - Notez bien que ces calculs de composantes doivent être faits pour toutes les forces qui sont obliques par rapport au repère choisi. Cela fait, vous additionnerez toutes les forces de type pour avoir la force totale agissant parallèlement à la pente horizontale et toutes les forces pour avoir la force totale agissant perpendiculairement à la pente.
- Pour mémoire, la formule du cosinus est :
-
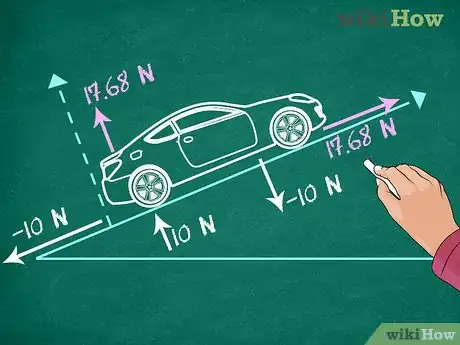
3Redessinez un schéma avec toutes les forces agissantes. À présent, vous êtes en mesure d’établir l’équilibre des forces s’exerçant sur votre objet. Vous ne devez indiquer que les forces parallèles à l’axe des ou des , il n’y a plus de forces obliques. Bien entendu, vous indiquerez le sens de chacune de ces forces, ainsi que leurs intensités.
- Dans notre exemple, la force de 25 N se décompose en deux forces de
17,68 N chacune, l’une perpendiculairement à la pente vers le haut, l’autre horizontalement vers la droite, toutes deux sont positives.
- Dans notre exemple, la force de 25 N se décompose en deux forces de
-
4Faites les sommes des forces agissant dans la même direction. En clair, additionnez les intensités des forces agissant dans le sens de l’axe des (parallèle à la pente) et celles perpendiculaires à ce même axe et donc parallèles à l’axe des . En faisant la somme des deux sommes, vous obtenez l’intensité des deux composantes de la résultante (). Une force étant un vecteur, elle est orientée : n’oubliez pas d’indiquer le sens des deux forces.
- La composante, selon l’axe des , de la résultante est :
. - La composante, selon l’axe des , de la résultante est :
.
- La composante, selon l’axe des , de la résultante est :
-
5Calculez l’intensité de la résultante. À ce stade, vous avez deux composantes : l’une dans le sens horizontal (axe des ), l’autre vertical (axe des ). L’intensité de la résultante est simplement l’hypoténuse des triangles rectangles formés par les deux composantes. À l’inverse de précédemment, vous chercherez la valeur de l’hypoténuse grâce au théorème de Pythagore : [8] .
- Appliqué à notre exemple, nous avons donc : et
- La formule de Pythagore s’établit comme suit :
. - Faites les calculs :
. - La voiture bougera sur ce plan incliné comme si elle était tirée vers le haut et la droite par une force de 19,28 N.
Publicité
Références
- ↑ http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Determining-the-Net-Force
- ↑ http://www.studyphysics.ca/newnotes/20/unit01_kinematicsdynamics/chp05_forces/lesson19.htm
- ↑ http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Determining-the-Net-Force
- ↑ http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Drawing-Free-Body-Diagrams
- ↑ http://study.com/academy/lesson/what-is-net-force-definition-magnitude-equations.html
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-3/Resolution-of-Forces
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-3/Resolution-of-Forces
- ↑ https://www.mathsisfun.com/pythagoras.html























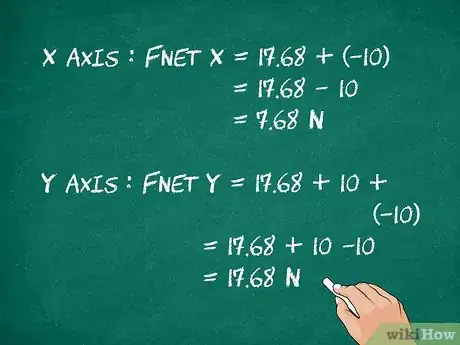


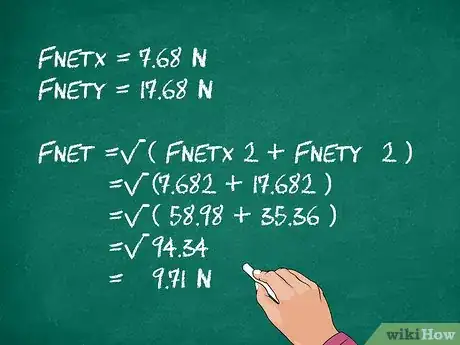

















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 7 555 fois.