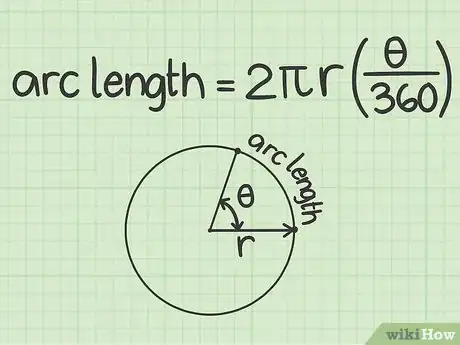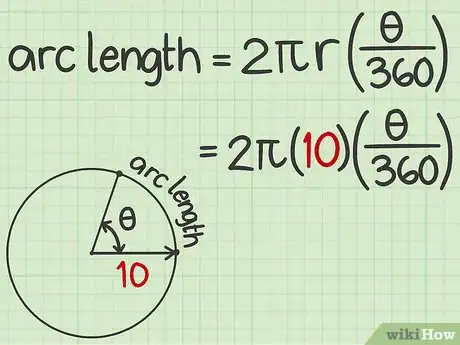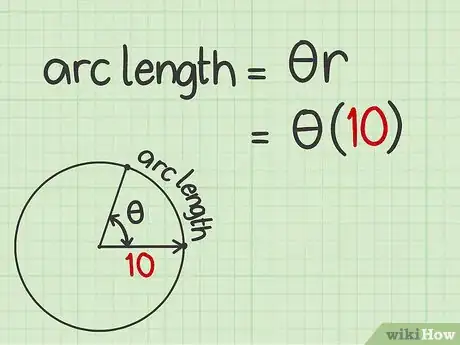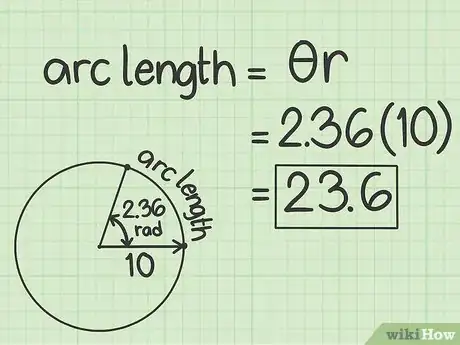Comment calculer la longueur d’un arc

Un arc de cercle est une partie de la circonférence de ce cercle ^{[1]
X
Source de recherche}. Deux points sur un cercle définissent deux arcs de cercle, un grand et un petit, à moins que les deux points ne soient opposés, auquel cas, ils sont égaux. La détermination de la longueur d'un arc de cercle suppose d'avoir quelques connaissances sur le cercle. Étant donné qu'un arc de cercle est une portion de la circonférence, à partir du moment où vous avez le rayon et le secteur angulaire (fraction de 360°) qui définit l'arc, vous pouvez trouver la longueur de ce dernier.

Méthode 1

Méthode 1 sur 2:
Trouver la longueur d'un arc avec un angle en degrés

1
Inscrivez la formule de la longueur de l'arc. La formule est la suivante : ${\text{L}}=2\pi (r)({\frac {\theta }{360}})$ , $L$ étant la longueur de l'arc, $r$ le rayon du cercle et $\theta$ , la mesure en degrés de l'angle de l'arc ^{[2]
X
Source de recherche}.
2
Remplacez le rayon du cercle par sa valeur. Cette valeur vous sera donnée dans l'énoncé ou vous devrez la mesurer sur la figure qui accompagne l'exercice. Faites bien attention à remplacer la bonne inconnue, soit $r$ $r$ .
- Ainsi, si le rayon de votre cercle est de 10 cm, votre formule se présentera sous la forme suivante : ${\text{L}}=2\pi (10)({\frac {\theta }{360}})$
3
Remplacez l'angle de l'arc par sa valeur. Cette valeur vous sera donnée dans l'énoncé ou vous devrez la mesurer avec un rapporteur sur la figure qui accompagne l'exercice. Pour cette formule, il faut impérativement une mesure de l'angle en degrés, et non en radians. Remplacez $\theta$ $\theta$ par sa vraie valeur.
- Ainsi, si l'angle de votre arc de cercle mesure 135°, votre formule sera la suivante : ${\text{L}}=2\pi (10)({\frac {135}{360}})$
4
Multipliez le rayon par $2\pi$ . Si vous faites le calcul à la main, prenez pour valeur de $\pi$ $\pi$ l' approximation courante, à savoir : $\pi =3,14$ $\pi =3,14$ . Récrivez alors la formule en sachant que $2\pi$ $2\pi$ est la valeur de la circonférence en radians ^{[3]
X
Source de recherche}.
- Reprenons notre exemple. Nous avons donc :
  $L=2\pi (10)({\frac {135}{360}})$
  $L=2(3,14)(10)({\frac {135}{360}})$
  $L=(62,8)({\frac {135}{360}})$
5
Divisez l'angle de l'arc par 360. Un cercle mesure 360°, lequel angle définit la circonférence, les deux éléments sont proportionnels. L'arc n'étant défini que par une portion de l'angle total, sa longueur (qui est une portion de la circonférence) sera proportionnelle à cet angle.
- Reprenons notre exemple. Nous avons donc :
  $L=(62,8)({\frac {135}{360}})$
  $L=(62,8)(0,375)$
6
Multipliez ces deux nombres. En faisant cette opération, vous obtenez la longueur de l'arc.
- Reprenons notre exemple. Nous avons donc :
  $L=(62,8)(0,375)$
  $L=23,55$
  En conclusion, la longueur (L) d'un arc de cercle, lequel a un rayon de 10 cm, défini par un secteur angulaire de 135°, est d'environ 23,55 cm.
Publicité

Méthode 2

Méthode 2 sur 2:
Trouver la longueur d'un arc avec un angle en radians

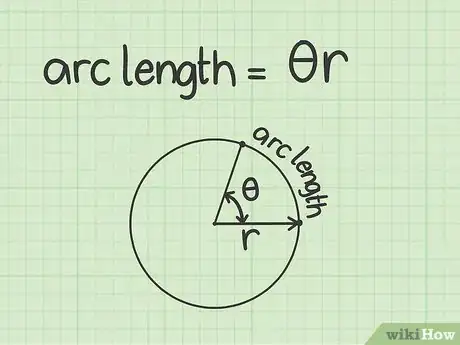
1
Inscrivez la formule de la longueur de l'arc. La formule est la suivante : ${\text{L}}=\theta (r)$ , $L$ étant la longueur de l'arc, $\theta$ la mesure de l'angle de l'arc en radians et $r$ , la longueur du rayon du cercle ^{[4]
X
Source de recherche}.
2
Remplacez la longueur du rayon par sa valeur. En effet, cette formule oblige à connaitre la valeur du rayon. Faites bien attention à remplacer la bonne inconnue, soit $r$ $r$ .
- Ainsi, si le rayon du cercle est de 10 cm, votre formule se présentera sous la forme suivante : ${\text{L}}=\theta (10)$
3
Remplacez la mesure de l'angle par sa valeur. Cette dernière doit impérativement être en radians. Si vous avez un angle en degrés, vous ne pouvez pas utiliser cette méthode, à moins de faire la conversion.
- Admettons que le secteur angulaire de l'arc soit de 2,36 rad, votre formule sera la suivante : ${\text{L}}=2,36(10)$
4
Multipliez le rayon par la mesure de l'angle en radians. Le résultat est tout bonnement la longueur de votre arc.
- Reprenons notre exemple. Nous avons donc :
  $L=2,36(10)$
  $L=23,6$
  En conclusion, la longueur d'un arc de cercle, lequel a un rayon de 10 cm, défini par un secteur angulaire de 2,36 rad, est d'environ 23,6 cm.
Publicité

Conseils

Si l'on vous donne, non pas le rayon, mais le diamètre du cercle, vous pouvez utiliser ces deux formules, sous condition de faire un petit calcul préalable. Pour rappel, ces formules utilisent le rayon du cercle. Le diamètre valant, par définition, deux fois le rayon, vous trouverez le rayon d'un cercle en divisant son diamètre par 2 ^{[5]
X
Source de recherche}. Admettons qu'on vous donne un cercle de 14 cm de diamètre (D), vous obtiendrez le rayon (r) en le divisant par 2 :
$R={\frac {D}{2}}={\frac {14}{2}}=7$
En conclusion, le rayon du cercle est de 7 cm.