Comment calculer la masse d’une sphère

Coécrit par l'équipe de wikiHow

En termes simples, une sphère est une balle solide et parfaitement ronde. Pour calculer sa masse, il faut connaitre sa taille (volume) et sa densité. Il est possible de calculer le volume en utilisant le rayon, la circonférence ou le diamètre. Vous pouvez également plonger une sphère dans l'eau pour mesurer son volume par déplacement. Si vous connaissez le volume, vous pouvez le multiplier par la densité pour trouver la masse du solide.

Partie 1

Partie 1 sur 3:
Déterminer le volume d'une sphère

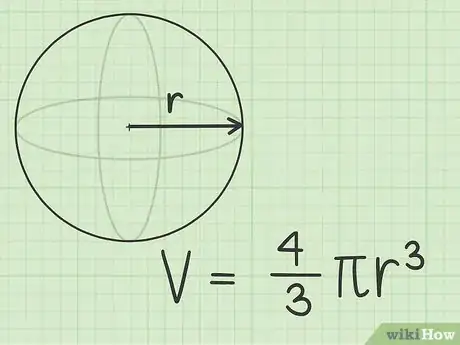
1
Rappelez-vous la formule utilisée pour calculer le volume d'une sphère. La sphère est un solide tridimensionnel de forme circulaire. La formule principale pour calculer le volume d'une sphère est la suivante ^{[1]
X
Source de recherche}.
- ${\text{Volume}}={\frac {4}{3}}\pi r^{3}$ ${\text{Volume}}={\frac {4}{3}}\pi r^{3}$
  - $\pi =3,14$
  - $r={\text{rayon}}$
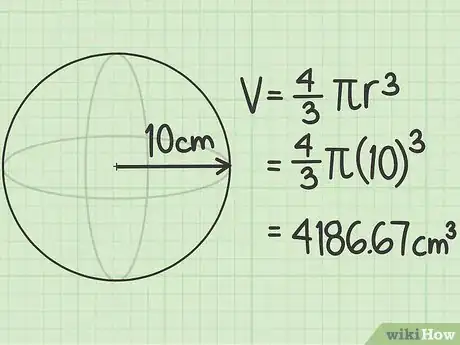
2
Déterminez le volume d'une sphère en connaissant le rayon. Le rayon d’une sphère est la distance entre son centre et n’importe quel point sur son bord extérieur. Si vous avez un problème mathématique dans lequel vous devez calculer le volume, il est probable que le rayon soit déjà donné. Dans le cas contraire, il sera difficile de le mesurer, parce que vous ne pouvez pas atteindre le centre d'un objet solide avec précision ^{[2]
X
Source de recherche}.
- Supposons que dans le problème il est indiqué que le rayon est de 10 cm. Calculez le volume comme suit :
  - ${\text{Volume}}={\frac {4}{3}}\pi r^{3}$
  - ${\text{Volume}}={\frac {4}{3}}*(3,14)*10^{3}$
  - ${\text{Volume}}=4,18667*1\ 000$
  - ${\text{Volume}}=4\ 186,67{\text{ cm}}^{3}$
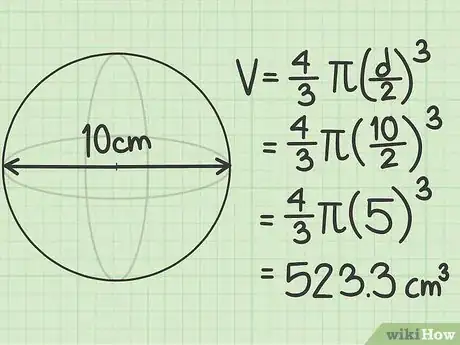
3
Déterminez le volume si le diamètre est connu. Le diamètre de la sphère peut être aussi spécifié dans votre problème. Le diamètre d'une sphère est le double de son rayon. En d’autres termes, le diamètre est la longueur d'un segment allant d'un bord de la sphère au bord opposé en passant par le centre. Pour calculer le volume à partir du diamètre (d), réécrivons la formule sous la forme suivante ^{[3]
X
Source de recherche}.
- ${\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}$
- Supposons que le diamètre de notre sphère est égal à 10 cm :
  - ${\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}$
  - ${\text{Volume}}={\frac {4}{3}}\pi ({\frac {10}{2}})^{3}$
  - ${\text{Volume}}={\frac {4}{3}}*(3,14)*(5^{3})$
  - ${\text{Volume}}=4,18667*125$
  - ${\text{Volume}}=523,3{\text{ cm}}^{3}$
4
Réécrivez la formule si vous connaissez la valeur de la circonférence. La circonférence d'une sphère est probablement la valeur la plus facile à mesurer directement. Vous pouvez utiliser un mètre à ruban : enroulez-le avec précaution autour de la partie la plus large et prenez juste la mesure. Sinon, il se peut que cette valeur soit déjà indiquée dans le problème. Pour trouver le volume d’une sphère à partir de sa circonférence (C), réécrivez la formule comme suit ^{[4]
X
Source de recherche} :
- ${\text{Volume}}={\frac {4}{3}}\pi r^{3}$
- ${\text{Volume}}={\frac {4}{3}}\pi *({\frac {C}{2\pi }})^{3}$
- ${\text{Volume}}={\frac {4}{3}}\pi *({\frac {C^{3}}{8\pi ^{3}}})$
- ${\text{Volume}}={\frac {C^{3}}{6\pi ^{2}}}$
5
Calculez le volume si la circonférence est connue. Supposons que vous avez une sphère dont la circonférence est de 32 centimètres. Trouvez son volume.
- ${\text{Volume}}={\frac {C^{3}}{6\pi ^{2}}}$
- ${\text{Volume}}={\frac {32^{3}}{6*3,14^{2}}}$
- ${\text{Volume}}={\frac {32,768}{59,158}}$
- ${\text{Volume}}=553,9{\text{ cm}}^{3}$
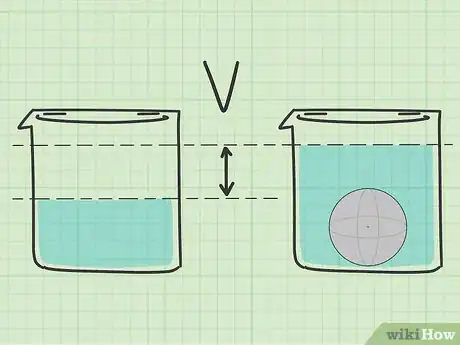
6
Mesurez le volume en observant son déplacement dans l’eau. Une autre méthode simple pour mesurer directement le volume d'une sphère est de plonger le solide dans l'eau. Il vous faudra un bécher suffisamment grand pour le contenir. Assurez-vous que le bécher est bien gradué ^{[5]
X
Source de recherche}.
- Versez assez d'eau dans le bécher. Notez la mesure.
- Plongez la sphère dans l'eau. Observez ensuite la montée du niveau de l'eau. Notez à nouveau la mesure.
- Soustrayez la première mesure de la seconde. Le résultat correspond au volume de la sphère.
  - Par exemple, supposons que le niveau de l'eau passe de 100 ml à 625 ml lorsque vous plongez le solide dans le liquide. Le volume est donc égal à 525 ml. Notez que 1 ml = 1 cm³.
Publicité

Partie 2

Partie 2 sur 3:
Calculer la masse à partir du volume

1
Trouvez la densité. Pour calculer la masse d’une sphère à partir du volume, il faut connaitre sa densité. Sachez que la densité varie selon le matériau utilisé. Par exemple, pour mieux comprendre ce concept, vous pouvez comparer le poids d'une sphère en polystyrène avec celui d'une sphère de même dimension, mais fabriqué en fer. Le fer a une densité plus élevée que le polystyrène et a également une masse plus grande.
- Vous pouvez trouver la densité des matériaux les plus courants en consultant des tableaux récapitulatifs en ligne, des manuels ou d'autres catalogues de produits industriels.
- Voici quelques exemples de matériaux avec leur densité ^{[6]
  X
  Source de recherche} :
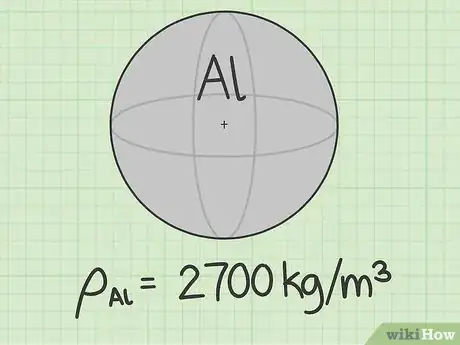
  - aluminium = 2 700 kg/m³
  - beurre = 870 kg/m³
  - plomb = 11,350 kg/m³
  - bois aggloméré = 190 kg/m³
2
Convertissez les unités de mesure au besoin. Les unités de mesure utilisées pour exprimer le volume d'un objet doivent correspondre à celles utilisées pour mesurer la densité du matériau avec lequel le solide est fabriqué. Sinon, une simple conversion est nécessaire.
- Les mesures de volume pour tous les exemples des sections précédentes ont été exprimées en centimètres cubes. Cependant, la densité des matériaux cités dans l’étape précédente est exprimée en mètres cubes, d’où la nécessité d’effectuer une conversion. Étant donné qu’un mètre équivaut à 100 cm, un mètre cube équivaut à 10⁶ centimètres cubes. Par conséquent, nous pouvons diviser les densités exprimées en mètres par le facteur de conversion 10⁶ afin de les exprimer en kg/cm³. Ce type de conversion est beaucoup plus facile à effectuer en déplaçant le séparateur décimal de 6 positions vers la gauche.
- Pour les quatre exemples de l’étape précédente, les densités converties sont les suivantes :
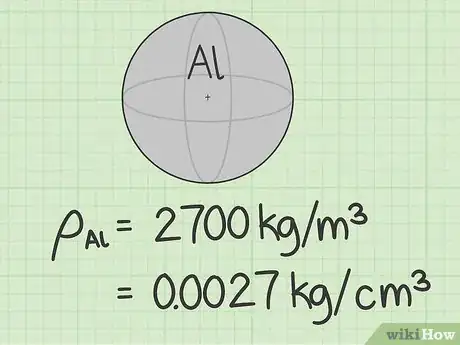
  - aluminium = 2 700 kg/m³ = 0,0027 kg/cm³
  - beurre = 870 kg/m³ = 0,00087 kg/cm³
  - plomb = 11,350 kg/m³ = 0,01135 kg/cm³
  - bois aggloméré = 190 kg/m³ = 0,00019 kg/cm³
3
Calculez la masse en multipliant le volume par la densité. La formule mathématique pour calculer la densité est la suivante : ${\text{Densité}}={\frac {\text{Masse}}{\text{Volume}}}$ ${\text{Densité}}={\frac {{\text{Masse}}}{{\text{Volume}}}}$ . En réécrivant l'équation pour calculer la masse, on obtient ceci : ${\text{Densité}}*{\text{Volume}}={\text{Masse}}$ ${\text{Densité}}*{\text{Volume}}={\text{Masse}}$ ^{[7]
X
Source de recherche}.
- En utilisant la densité des quatre matériaux de notre exemple, calculez la masse d'une sphère dont le volume est égal à 500 cm³.
  - ${\text{Aluminium}}:500{\text{ cm}}^{3}*0,0027{\frac {\text{kg}}{{\text{cm}}^{3}}}=1,35{\text{ kg}}$
  - ${\text{Beurre}}:500{\text{ cm}}^{3}*0,00087{\frac {\text{kg}}{{\text{cm}}^{3}}}=0,435{\text{ kg}}$
  - ${\text{Plomb}}:500{\text{ cm}}^{3}*0,01135{\frac {\text{kg}}{{\text{cm}}^{3}}}=5,675{\text{ kg}}$
  - ${\text{Bois aggloméré}}:500{\text{ cm}}^{3}*0,00019{\frac {\text{kg}}{{\text{cm}}^{3}}}=0,095{\text{ kg}}$
Publicité

Partie 3

Partie 3 sur 3:
Résoudre un problème simple

1
Lisez attentivement le problème. Lorsque vous résolvez un problème lié au calcul de masse, il est nécessaire de lire attentivement l'énoncé. Au fur et à mesure que vous lisez le texte, il peut être utile de souligner les données pertinentes. Prenez le temps de lire tout le texte afin d'avoir une idée claire de la consigne. À titre d’exemple, considérons le problème suivant.
- Une grande sphère en laiton massif a un diamètre de 1,2 m. Calculez la masse de ce solide.
2
Identifiez les données connues et inconnues. En lisant attentivement notre exemple, vous remarquerez que le diamètre de la sphère est déjà indiqué dans le problème. Il vous suffit donc de réécrire la formule.
- ${\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}$
- Vous devriez également avoir remarqué que la sphère de notre problème est en laiton. Recherchez alors la densité du laiton à partir d'un tableau de densité sur Internet.
  - En accédant à l'un des nombreux sites Web traitant de ce type d'information, vous verrez que la densité du laiton est de 8 480 kg/m³. Puisque le diamètre de la sphère en question est exprimé en mètres, son volume sera exprimé en mètres cubes. Par conséquent, il ne sera pas nécessaire d'effectuer une conversion de la densité.
3
Calculez le volume. Utilisez la formule correcte parmi celles indiquées dans cet article, puis remplacez les variables par les données et effectuez les calculs comme indiqué ci-dessous :
- ${\text{Volume}}={\frac {4}{3}}\pi ({\frac {d}{2}})^{3}$
- ${\text{Volume}}={\frac {4}{3}}\pi ({\frac {1,2}{2}})^{3}$
- ${\text{Volume}}=4,18667*0,6^{3}$
- ${\text{Volume}}=4,18667*0,216$
- ${\text{Volume}}=0,90432{\text{ m}}^{3}$
4
Utilisez la densité du laiton pour calculer la masse. Rappelez-vous que la formule pour calculer la masse est la suivante ${\text{Masse}}={\text{Densité}}*{\text{Volume}}$ ${\text{Masse}}={\text{Densité}}*{\text{Volume}}$ ^{[8]
X
Source de recherche}. Remplacez les variables de la formule par les valeurs numériques relatives pour trouver la masse.
- ${\text{Masse}}={\text{Densité}}*{\text{Volume}}$
- ${\text{Masse}}=8\ 480{\frac {\text{ kg}}{{\text{ m}}^{3}}}*0,90432{\text{ m}}^{3}$
- ${\text{Masse}}=7\ 668,6{\text{ kg}}$
Publicité

Conseils

Une des informations de base à considérer comme hypothèse initiale est que la densité d’une sphère est uniforme à chaque point du solide. Dans la plupart des problèmes de mathématiques et de physique, cette hypothèse sera vraie. Cependant, en réalité, il est possible que la sphère soit composée d'un noyau intérieur constitué d'un matériau différent de celui avec lequel la surface extérieure a été construite. Dans ce cas, la densité des deux matériaux sera très probablement différente.