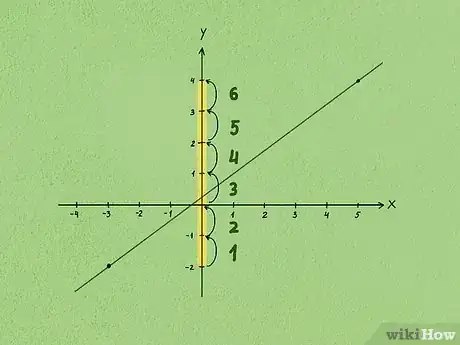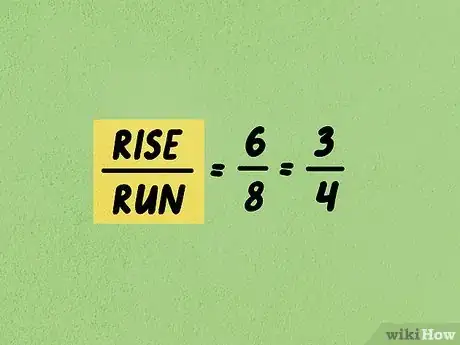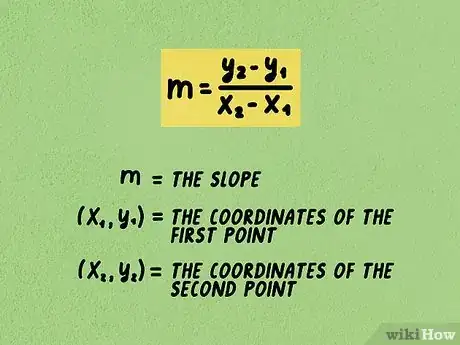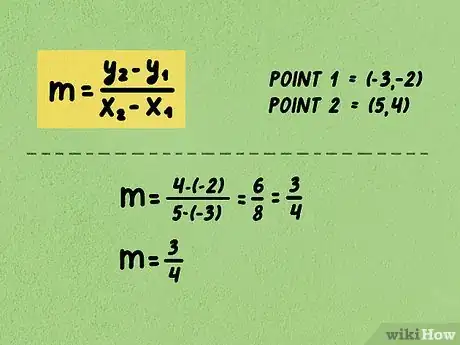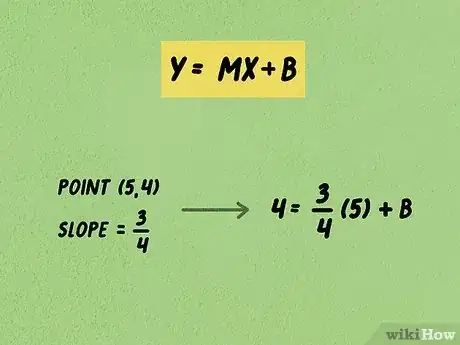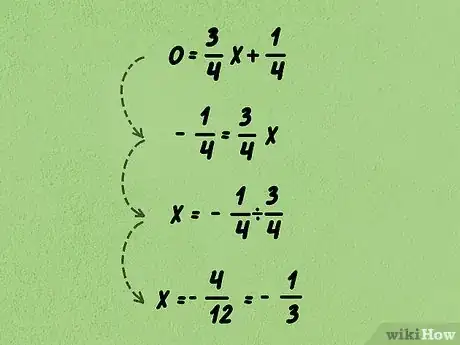Comment calculer la pente et les points d'intersection d'une droite

La pente d'une droite est le rapport de son déplacement vertical sur son déplacement horizontal ^{[1]
X
Source de recherche}. C'est en quelque sorte son inclinaison par rapport à l'horizontale. Savoir calculer une pente et trouver les points d'intersection d'une droite avec les principaux axes est important en mathématiques, mais aussi dans d'autres domaines, comme l'économie ^{[2]
X
Source de recherche}, les géosciences ^{[3]
X
Source de recherche} ou encore la finance.

Méthode 1

Méthode 1 sur 4:
Utiliser le graphe d'une droite pour trouver la pente

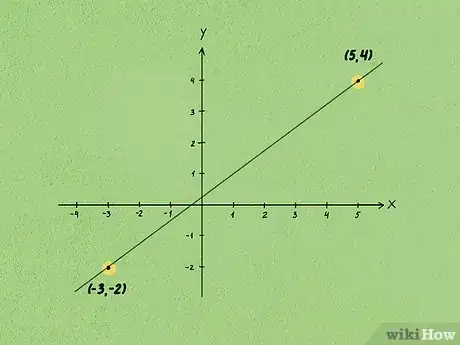
1
Matérialisez deux points sur la droite. Prenez deux points quelconques de la droite et repérez-les par deux points. Notez leurs coordonnées respectives.
- Pour les coordonnées, vous noterez entre parenthèses en premier l'abscisse, puis l'ordonnée.
- Prenez, par exemple, les deux points de coordonnées (-3, -2) et (5, 4).
2
Déterminez le déplacement vertical entre ces points. Rien de plus simple, faites la différence des ordonnées ( $y$ $y$ ). Partez du point le plus bas et comptez vers le haut l'écart vertical (en unités du repère) avec le point placé plus haut.
- La pente peut être positive comme négative. Si vous comptez vers le bas, l'écart sera négatif, sinon l'écart est positif (déplacement vers le haut ^{[4]
  X
  Source de recherche}). Si la droite monte vers la droite, le déplacement vertical est positif. Si la droite descend vers la droite, le déplacement vertical est négatif ^{[5]
  X
  Source de recherche}.
- Dans notre exemple, l'ordonnée du premier est -2 et celle du second, 4. L'écart entre les deux est donc de : 2 + 4, soit 6. Dans ce cas, le déplacement vertical est donc de 6 unités.
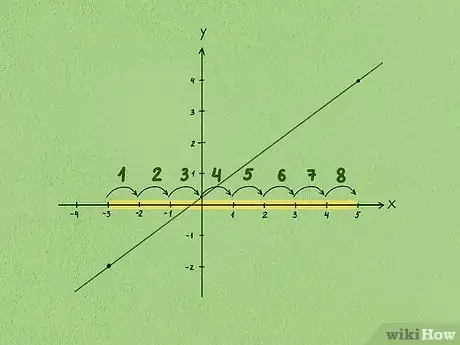
3
Déterminez le déplacement horizontal entre ces points. Faites la différence des abscisses ( $x$ $x$ ). Partez du point le plus à gauche et comptez vers la droite l'écart horizontal (en unités du repère) avec le point placé le plus à droite.
- Un déplacement horizontal est par convention toujours positif, car on compte toujours de la gauche vers la droite, jamais dans l'autre sens ^{[6]
  X
  Source de recherche}.
- Dans notre exemple, l'abscisse du premier point est -3 et celle du second, 5. L'écart entre les deux est donc de : 3 + 5, soit 8. Dans ce cas, le déplacement horizontal est donc de 8 unités.
4
Calculez la pente. C'est tout simplement, comme cela a été dit plus haut, le rapport du déplacement vertical sur le déplacement horizontal. La pente peut être exprimée sous la forme d'une fraction, mais aussi d'un entier si la fraction se simplifie.
- Dans l'exemple, vous aviez un déplacement vertical de 6 et un déplacement horizontal de 8, la pente est donc de : ${\frac {6}{8}}$ , soit, après simplification, ${\frac {3}{4}}$ .
Publicité

Méthode 2

Méthode 2 sur 4:
Utiliser deux points pour trouver la pente d'une droite

1
Posez la formule de calcul $m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Dans cette formule, $m$ $m$ est la pente, $(x_{1},y_{1})$ $(x_{{1}},y_{{1}})$ , les coordonnées du premier point et $(x_{2},y_{2})$ $(x_{{2}},y_{{2}})$ , les coordonnées du second point.
- Pour rappel, la formule de la pente $m$ est la suivante : $m={\frac {d{\acute {e}}placement\ vertical}{d{\acute {e}}placement\ horizontal}}$ . La pente compare l'écart d'ordonnées à l'écart d'abscisses ^{[7]
  X
  Source de recherche}.
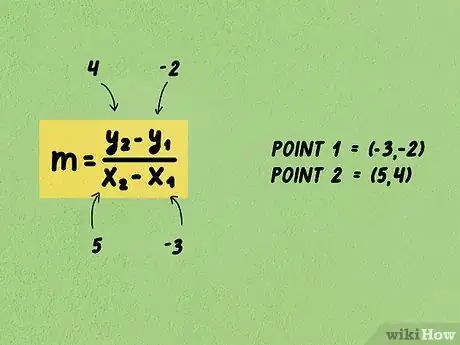
2
Faites l'application numérique. Dans la formule, remplacez les coordonnées des deux points en faisant attention à ne pas les mélanger. Les coordonnées $(x_{1},y_{1})$ $(x_{{1}},y_{{1}})$ sont celles du premier point, $(x_{2},y_{2})$ $(x_{{2}},y_{{2}})$ , celles du second. Si vous inversez ou mélangez, vous n'aurez pas la bonne pente.
- Reprenons les deux points donnés plus haut, à savoir (-3, -2) et (5, 4). La formule de la pente est la suivante : $m={\frac {4-(-2)}{5-(-3)}}$ .
3
Faites les calculs. En fin de calcul, simplifiez éventuellement la fraction. La pente peut être exprimée sous la forme d'une fraction, mais aussi d'un entier si la fraction se simplifie.
- Dans l'exemple, la pente $m$ est : $m={\frac {4-(-2)}{5-(-3)}}$ . Le numérateur est alors : $4-(-2)=6$ . Soustraire un nombre négatif revient à ajouter son opposé positif. Quant au dénominateur, il est : $5-(-3)=8$ . Vous avez donc ${\frac {6}{8}}$ qui se simplifie en ${\frac {3}{4}}$ . La pente est de $m={\frac {3}{4}}$ .
Publicité

Méthode 3

Méthode 3 sur 4:
Trouver l'ordonnée à l'origine

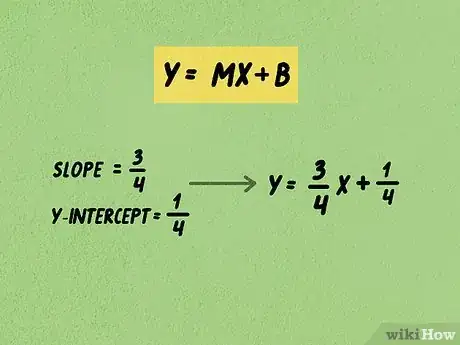
1
Posez la formule de calcul $y=mx+b$ . Dans cette formule, $y$ $y$ est l'ordonnée de n'importe quel point de la droite, $x$ $x$ , l'abscisse de ce même point et $m$ $m$ , la pente. Quant à $b$ $b$ , c'est l'ordonnée à l'origine (quand $x=0$ $x=0$ ).
- Toute équation de la forme $y=mx+b$ est celle d'une fonction affine ^{[8]
  X
  Source de recherche}.
- L'ordonnée à l'origine est celle du point d'intersection avec l'axe des ordonnées (axe des $y$ ), quand $x=0$ .
CONSEIL D'EXPERT(E)

Grace Imson, MA
Professeure de mathématiques au City College of San Francisco
Grace Imson est une professeure de mathématiques ayant plus de 40 ans d'expérience dans l’enseignement. Grace exerce actuellement au City College de San Francisco. Auparavant, elle était professeure au département de mathématiques de l'université Saint-Louis. Elle a enseigné cette discipline aux niveaux primaire, intermédiaire, secondaire et universitaire. Elle est titulaire d'un master en éducation avec une spécialisation en administration et supervision, délivré par l'université Saint-Louis.

Grace Imson, MA
Professeure de mathématiques au City College of San Francisco

Notre experte confirme : « Si vous avez la pente (m) et un point (x,y) d'une droite, son équation est : y = mx + b. Connaissant m, x et y, il est alors facile de calculer b, l'ordonnée à l'origine. »
2
Faites l'application numérique. Dans la formule, remplacez $m$ $m$ , $x$ $x$ et $y$ $y$ par leurs valeurs respectives, ces deux dernières valeurs étant celles d'un point de la droite. Quant à $m$ $m$ , soit elle vous a été donnée dans l'exercice ou le problème soit vous l'avez calculée comme cela a été vu précédemment.
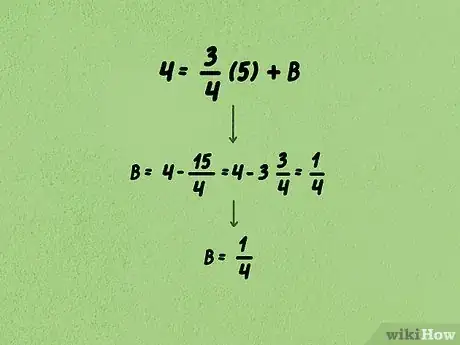
- Nous avions précédemment une pente de ${\frac {3}{4}}$ et le point de coordonnées (5,4). Remplaçons les valeurs dans la formule et nous obtenons : $4={\frac {3}{4}}(5)+b$ .
3
Calculez $b$ . Il ne vous reste plus qu'à trouver l'inconnue $b$ $b$ . Pour cela, multipliez en premier la pente par l'abscisse. Soustrayez enfin ce résultat des deux côtés de l'équation.
- Dans notre exemple, l'équation devient : $4={\frac {15}{4}}+b$ . Soustrayez ${\frac {15}{4}}$ de chaque côté et vous obtenez : $b=4-{\frac {15}{4}}$ , soit $b={\frac {16}{4}}-{\frac {15}{4}}={\frac {1}{4}}$ . L'ordonnée à l'origine ( $y$ en $x=0$ ) de cette droite est ${\frac {1}{4}}$ .
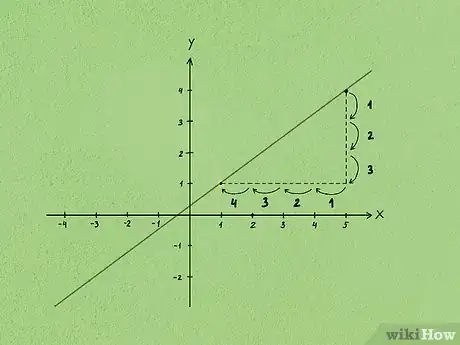
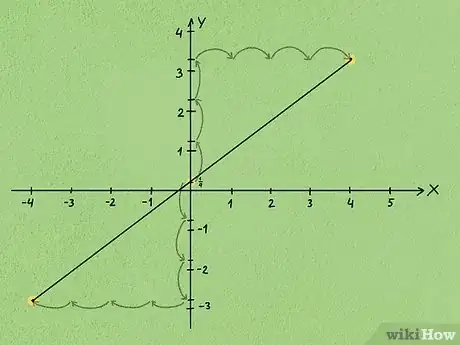
4
Vérifiez graphiquement vos calculs. Dans un repère orthonormé, placez le point en question, tracez la droite à partir de ce point en respectant la pente. L'ordonnée à l'origine est celle du point d'intersection de cette droite avec l'axe des ordonnées.
- Nous avions une pente de ${\frac {3}{4}}$ et le point (5,4). Tracez le point au bon endroit, comptez depuis celui-ci 3 unités vers la gauche et 4 unités vers le bas, placez un point. Tracez la droite entre ces deux points et voyez où cette droite coupe l'axe des ordonnées. Ici, c'est juste au-dessus du point origine (0,0).
Publicité

Méthode 4

Méthode 4 sur 4:
Trouver l'abscisse à l'origine

1
Posez la formule de calcul $y=mx+b$ . Dans cette formule, $y$ $y$ est l'ordonnée de n'importe quel point de la droite, $x$ $x$ , l'abscisse de ce même point et $m$ $m$ , la pente. Quant à $b$ $b$ , c'est l'ordonnée à l'origine (quand $x=0$ $x=0$ ).
- Une équation de la forme $y=mx+b$ est celle d'une fonction affine ^{[9]
  X
  Source de recherche}.
- L'abscisse à l'origine est celle du point d'intersection avec l'axe des abscisses (axe des $x$ ), quand $y=0$ .
2
Faites l'application numérique. Dans la formule, remplacez $m$ $m$ et $b$ $b$ par leurs valeurs respectives. Concernant la pente $m$ $m$ , soit elle vous a été donnée dans l'exercice ou le problème soit vous l'avez calculée comme cela a été vu précédemment.
- Prenons l'exemple d'une droite dont la pente est de ${\frac {3}{4}}$ et l'ordonnée à l'origine de ${\frac {1}{4}}$ , la formule devient la suivante : $y={\frac {3}{4}}x+{\frac {1}{4}}$ .
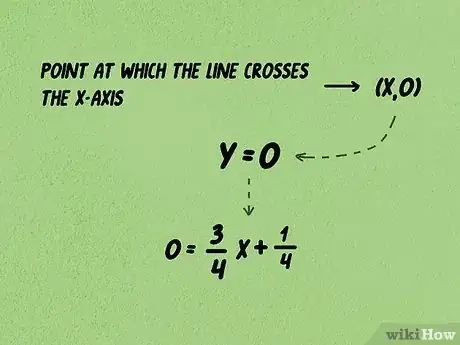
3
Remplacez $y$ par 0 ^{[10]
X
Source de recherche}. Vous cherchez cette fois l'abscisse à l'origine, c'est-à-dire celle du point d'intersection de la droite avec l'axe des abscisses. L'ordonnée $y$ $y$ de ce point est par définition 0. C'est pourquoi vous devez remplacer $y$ $y$ par 0, il vous restera une seule inconnue à trouver : $x$ $x$ . Vous trouverez alors le point de coordonnées (x,0).
- Reprenons l'exemple précédent. La formule devient : $0={\frac {3}{4}}x+{\frac {1}{4}}$ .
4
Calculez $x$ . Soustrayez de chaque côté par l'ordonnée à l'origine. Divisez ensuite chaque membre par la pente.
- Dans notre cas concret, cela donne : ${\frac {-1}{4}}={\frac {3}{4}}x$ . Divisez de chaque côté par ${\frac {3}{4}}$ ou multipliez, ce qui revient au même, ${\frac {4}{3}}$ . Vous avez alors : $x={\frac {-1}{4}}\times {\frac {4}{3}}={\frac {-1\times 4}{4\times 3}}={\frac {4}{12}}={\frac {-1}{3}}$ . Le point d'intersection de la droite avec l'axe des abscisses est $({\frac {-1}{3}},0)$ . L'abscisse à l'origine est donc ${\frac {-1}{3}}$ .
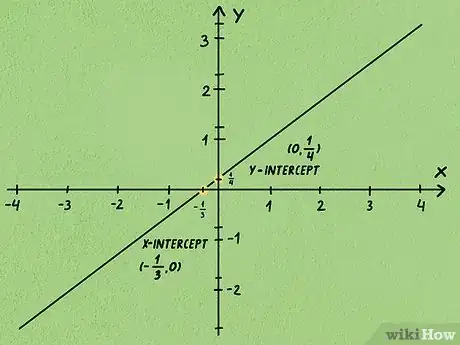
5
Vérifiez graphiquement vos calculs. Dans un repère orthonormé, placez le point d'intersection avec l'axe des ordonnées, tracez la droite à partir de ce point en respectant la pente. L'abscisse à l'origine est celle du point d'intersection de cette droite avec l'axe des abscisses.
- Nous avons une pente de ${\frac {3}{4}}$ et les coordonnées du point d'intersection, soit $(0,{\frac {1}{4}})$ . Faites figurer ce point, comptez depuis celui-ci 3 unités vers la gauche et 4 unités vers le bas, placez un second point. Tracez la droite entre ces deux points et voyez où cette droite coupe l'axe des abscisses : dans ce cas, c'est juste à gauche du point origine (0,0).
6
Voyez ce que cela donne graphiquement.

Publicité