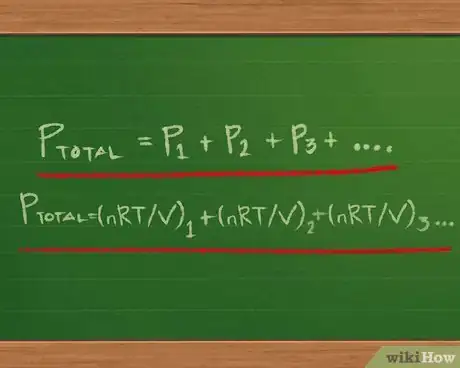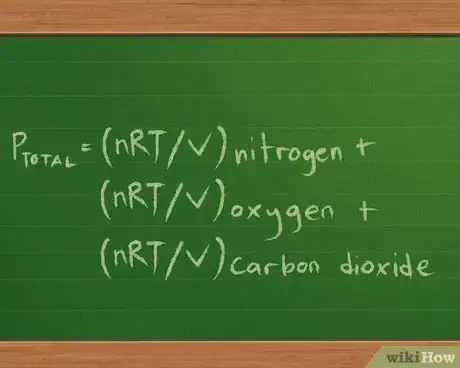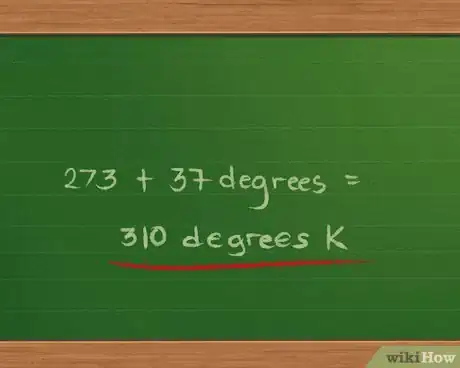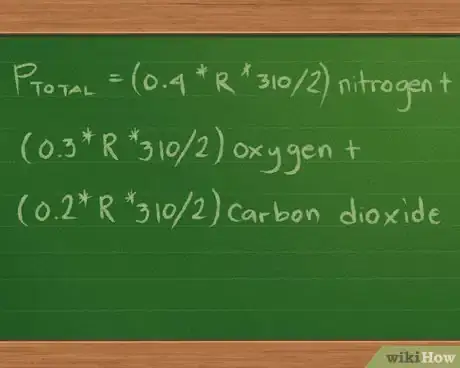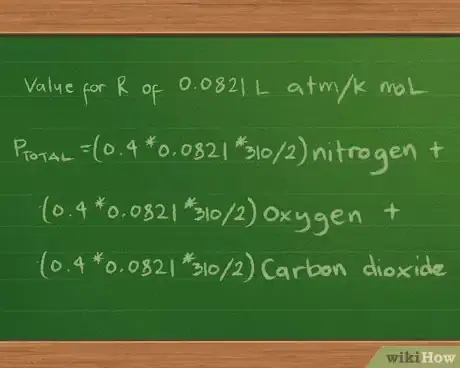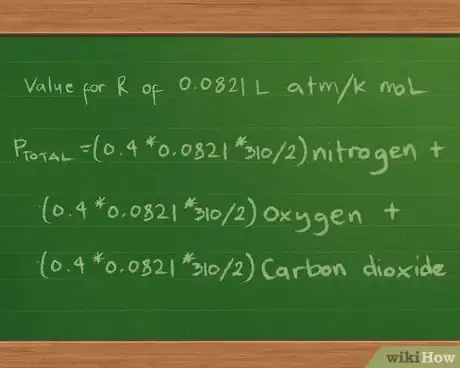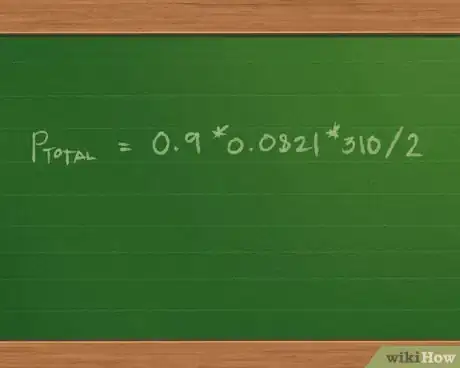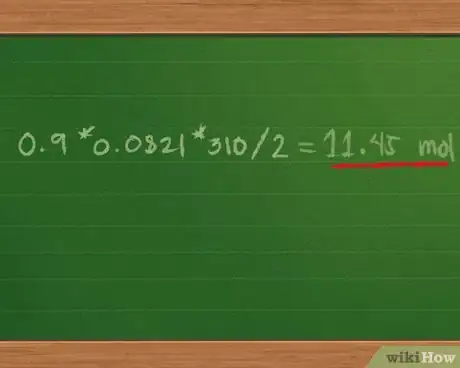Comment calculer la pression partielle

En chimie, on désigne sous le terme de « pression partielle » la pression que chaque gaz, dans un mélange, exerce sur son environnement, par exemple au sein d'un échantillon dans une fiole, dans la bouteille d'un plongeur ou bien sur les parois de l'atmosphère. Il est possible de calculer la pression de chaque gaz du mélange à condition de savoir en quelle quantité il est présent, le volume qu'il occupe, ainsi que sa température. Il suffit ensuite d'ajouter toutes les pressions partielles pour trouver la pression totale. Vous pouvez aussi commencer par chercher la pression totale et en déduire les pressions partielles.

Partie 1

Partie 1 sur 3:
Comprendre les propriétés des gaz

1
Considérez chaque gaz comme « idéal ». En chimie, on appelle gaz idéal un gaz qui n'interagit pas avec les autres, qui n'est pas attiré par leurs molécules. Toutes les molécules peuvent se percuter et rouler les unes sur les autres comme des boules de billard sans jamais en aucune façon être transformées par ce contact ^{[1]
X
Source de recherche}.
- La pression d'un gaz idéal augmente quand il est comprimé dans un espace réduit et diminue quand il se dilate dans un espace plus grand. Ce phénomène est aussi connu sous le nom de loi de Boyle, en l'honneur de Robert Boyle. Mathématiquement, cela donne la formule k = P x V ou, plus simplement, k = PV, k étant une constante, P la pression et V le volume ^{[2]
  X
  Source de recherche}.
- Les mesures de pression peuvent être exprimées avec diverses unités. Parmi elles, il y a le Pascal (Pa), qui est par définition la force exercée par un Newton sur un mètre carré. Il existe également l'atmosphère (atm), que l'on définit comme la pression exercée par l'atmosphère terrestre au niveau de la mer. 1 atm équivaut à 101,325 Pa ^{[3]
  X
  Source de recherche}.
- La température d'un gaz idéal augmente quand son volume augmente et baisse quand son volume diminue. Ce phénomène est aussi connu sous le nom de loi de Charles, en l'honneur de Jacques Charles. Mathématiquement, cela donne k = V / T, où k est la constante qui lie le volume et la température, V le volume et T la température ^{[4]
  X
  Source de recherche}.
- Dans cette équation, la température des gaz doit être exprimée en degrés Kelvin, c'est-à-dire qu'il faut rajouter 273 degrés à la mesure en degrés Celsius.
- Ces deux équations peuvent être combinées en une seule : k = PV / T, qui peut également s'écrire PV = kT.
2
Vérifiez le mode d'expression de la quantité de gaz. Un gaz possède toujours un volume et une masse. Si le volume est en général exprimé en litres (L), il faut savoir que la masse peut l'être de deux manières distinctes.
- Habituellement, on mesure les masses en grammes ou en kilogrammes si elles sont importantes.
- Étant donné que les masses des gaz sont habituellement très faibles, celles-ci sont souvent exprimées d'une autre façon. On utilise généralement la masse moléculaire ou masse molaire. La masse molaire est la somme des masses atomiques de chaque atome dont le gaz est composé, chacun d'entre eux étant comparé à la valeur de référence de 12 pour le carbone ^{[5]
  X
  Source de recherche}.
- Les atomes et les molécules sont des particules trop petites pour que l'on puisse travailler avec. C'est pour cela que les quantités de gaz sont exprimées en moles. On peut calculer le nombre de moles se trouvant dans un gaz donné en divisant sa masse par sa masse molaire. Le nombre de moles est alors symbolisé par la lettre n.
- Dans l'équation, on peut remplacer la constance k par le produit de n (le nombre de moles) et de R, une nouvelle constante. On obtient dès lors nR = PV/T ou bien PV = nRT ^{[6]
  X
  Source de recherche}.
- La valeur de R dépendra des unités dans lesquelles sont mesurés la pression gazeuse, le volume et la température. Si le volume est en litres, la température en degrés Kelvin et la pression en atmosphères, R vaut 0,0821 L atm/K mol. On peut également l'écrire 0,0821 L atm K^-1 mol ^-1 pour éviter d'avoir une division dans l'unité de mesure ^{[7]
  X
  Source de recherche}.
3
Comprenez la loi de Dalton sur la pression partielle. La loi de Dalton a été rédigée par le physicien et chimiste John Dalton, qui a été le premier à défendre la thèse selon laquelle les substances chimiques étaient composées d'atomes ^{[8]
X
Source de recherche}^{[9]
X
Source de recherche}^{[10]
X
Source de recherche}. Cette loi énonce que la pression totale d'un mélange gazeux est égale à la somme des pressions de chacun des gaz contenus dans le mélange.
- L'équation de la loi de Dalton est P_totale = P₁ + P₂ + P₃… On peut rajouter autant d'éléments après le signe égal qu'il y a de gaz différents dans le mélange.
- La loi de Dalton peut également servir pour les gaz dont on ne connait pas les pressions partielles, mais dont les températures et les volumes sont donnés. La pression partielle d'un gaz est la même que si la même quantité de ce gaz se trouvait dans le même volume sans qu'il ne soit mélangé à rien d'autre ^{[11]
  X
  Source de recherche}.
- Il est possible de réécrire l'équation pour chacune des pressions partielles de telle sorte qu'au lieu d'avoir PV = nRT, il n'y ait que P dans la partie gauche de l'équation. Pour cela, il faut diviser les deux côtés par V : PV/V = nRT/V. Les deux V à droite s'annulent, il nous reste P = nRT/V.
- Il ne nous reste plus alors qu'à remplacer P dans la première partie de l'équation consacrée aux pressions partielles : P_totale =(nRT/V) ₁ + (nRT/V) ₂ + (nRT/V) ₃…
Publicité

Partie 2

Partie 2 sur 3:
Calculer les pressions partielles puis la pression totale

1
Utilisez l'équation avec les gaz étudiés. Nous allons ici prendre pour exemple un contenant de 2 litres qui contient 3 gaz différents : de l'azote (N₂), de l'oxygène (O₂) et du dioxyde de carbone (CO₂). Nous avons 10 grammes de chacun de ces gaz, qui sont à une température de 37 °C. Nous devons chercher la pression partielle pour chacun d'entre eux, puis en déduire la pression que le mélange exerce sur les parois du contenant.
- Notre équation pour la pression partielle sera donc P_totale = P_azote + P_oxygène + P_{dioxyde de carbone}.
- Étant donné que nous connaissons le volume et la température et que nous sommes en mesure de calculer le nombre de moles de chaque gaz grâce à la masse, nous pouvons réécrire l'équation ainsi pour chercher la pression que chacun d'eux exerce : P_totale =(nRT/V) _azote + (nRT/V) _oxygène + (nRT/V) _{dioxyde de carbone}.
2
Convertissez la température en degrés Kelvin. Le gaz est à 37 °C, nous ajoutons 273 et nous obtenons 310 degrés K.
3
Trouvez le nombre de moles. Pour cela, il faut prendre la masse de chaque gaz et la diviser par sa masse molaire ^{[12]
X
Source de recherche}, que nous avons déjà définie comme étant la somme des masses atomiques de chaque atome du composé.
- La masse atomique d'un atome de notre premier gaz, l'azote (N₂), est de 14. Comme l'azote est un gaz diatomique (ses molécules sont formées de deux atomes), il faut multiplier cette valeur par deux. Nous en arrivons donc à la conclusion que la masse molaire d'azote dans notre échantillon est de 28. Il ne nous reste plus qu'à diviser la masse en grammes (10 g) par 28 pour obtenir le nombre de mole. Notre échantillon contient environ 0,4 mol d'azote.
- La masse atomique d'un atome de notre deuxième gaz, l'oxygène (O₂), est de 16. Il s'agit également d'un gaz diatomique, nous multiplions donc 16 par 2 pour en déduire que la masse molaire d'oxygène dans l'échantillon est de 32. Nous divisons 10 g par 32 et concluons qu'il y a environ 0,3 mol d'oxygène dans notre contenant.
- Notre troisième gaz, le dioxyde de carbone (CO₂), possède 3 atomes : deux d'oxygène (ayant chacun une masse atomique de 16) et un de carbone (ayant une masse atomique de 12). Nous ajoutons ces trois masses pour trouver la masse molaire : 12 + 16 + 16 = 44. En divisant 10 g par 44, nous arrivons à 0,2 mol de dioxyde de carbone.
4
Intégrez les valeurs. Entrez les valeurs connues du volume, de la température et du nombre de moles dans l'équation. Celle-ci devient donc : P_totale = (0,4*R*310/2) _azote + (0,3*R*310/2) _oxygène + (0,2*R*310/2) _{dioxyde de carbone}.
- Pour simplifier l'écriture, nous avons supprimé toutes les unités qui accompagnaient les valeurs. Elles disparaissent lorsque nous faisons le calcul, il ne nous restera que l'unité de mesure qui sert à exprimer la pression.
5
Introduisez la valeur de la constante R. Comme nous exprimerons les pressions partielles et la pression totale en atmosphères, nous prendrons la valeur 0,0821 L atm/K mol pour R. Nous arrivons alors à l'équation P_totale =(0,4*0,0821*310/2) _azote + (0,3*0,0821*310/2) _oxygène + (0,2*0,0821*310/2) _{dioxyde de carbone}.
6
Calculez la pression partielle de chaque gaz. Maintenant que toutes nos données sont à leurs places, il est temps de passer aux calculs.
- Pour la pression partielle de l'azote, nous multiplions 0,4 mol par la constante 0,0821 et par la température de 310 degrés K, puis nous divisons par 2 litres : 0,4*0,0821*310/2 = 5,09 atm environ.
- Pour la pression partielle de l'oxygène, nous multiplions 0,3 mol par la constante 0,0821 et par la température de 310 degrés K, puis nous divisons par 2 litres : 0,3*0,0821*310/2 = 3,82 atm environ.
- Pour la pression partielle du dioxyde de carbone, nous multiplions 0,2 mol par la constante 0,0821 et par la température de 310 degrés K, puis nous divisons par 2 litres : 0,2*0,0821*310/2 = 2,54 atm environ.
- Nous pouvons alors additionner ces trois pressions pour trouver la pression totale : P_totale = 5,09 + 3,82 + 2,54. La pression totale vaut donc environ 11,45 atm.
Publicité

Partie 3

Partie 3 sur 3:
Calculer la pression totale puis les pressions partielles

1
Reprenez l'équation des pressions partielles. Nous utilisons le même exemple, nous avons toujours un échantillon de 2 litres contenant de l'azote (N₂), de l'oxygène (O₂) et du dioxyde de carbone (CO₂). L'échantillon est à 37 °C et il y a 10 g de chaque gaz.
- La température en Kelvin est toujours de 310 degrés et comme nous l'avons calculé précédemment, nous avons environ 0,4 mol d'azote, 0,3 mol d'oxygène et 0,2 mol de dioxyde de carbone.
- Nous exprimons toujours les pressions en atmosphères, ce qui signifie que la constante R a toujours une valeur de 0,0821 L atm/K mol.
- À cette étape du raisonnement, notre équation est toujours la même : P_totale =(0,4*0,0821*310/2) _azote + (0,3*0,0821*310/2) _oxygène + (0,2*0,0821*310/2) _{dioxyde de carbone}.
2
Cherchez le nombre total de moles du mélange. Pour cela, vous devez ajouter le nombre de moles de chaque gaz. Comme chaque masse molaire est multipliée par la même constante et que la température et le volume sont bien entendu identiques pour les trois gaz, nous pouvons nous servir de la propriété mathématique de distributivité pour réécrire l'équation sous la forme P_totale = (0,4 + 0,3 + 0,2)*0,0821*310/2.
- Additionnez : 0,4 + 0,3 + 0,2 = 0,9 mol de mélange gazeux. L'équation est simplifiée et devient P_totale = 0,9*0,0821*310/2.
3
Trouvez la pression totale du mélange. 0,9*0,0821*310/2 = 11,45 atm environ.
4
Cherchez la proportion de chaque gaz dans le mélange. Pour cela, divisez le nombre de moles d'un gaz par le nombre total de moles de l'échantillon.
- Il y a 0,4 mol d'azote, 0,4/0,9 = 0,44. Il compose donc environ 44 pour cent du mélange.
- Il y a 0,3 mol d'oxygène, 0,3/0,9 = 0,33. Il compose donc environ 33 pour cent du mélange.
- Il y a 0,2 mol de dioxyde de carbone, 0,2/0,9 = 0,22. Il compose donc environ 22 pour cent du mélange.
- La somme des trois proportions ci-dessus donne 0,99. En fait, les décimales se répètent indéfiniment, il y a en réalité un nombre infini de 9 après la virgule du résultat total. Par définition, cela revient au même qu'un résultat de 1, qui équivaut à 100 pour cent.
5
Calculez la pression partielle. Il suffit de multiplier la proportion de chaque gaz dans le mélange par la pression totale pour l'obtenir.
- 0,44*11,45 = 5,04 atm environ.
- 0,33*11,45 = 3,78 atm environ.
- 0,22*11,45 = 2,52 atm environ.
Publicité

Conseils

Vous remarquerez qu'il y a de légères différences entre les valeurs que l'on trouve en cherchant d'abord les pressions partielles pour en déduire ensuite la pression totale et les valeurs que l'on obtient en cherchant d'abord la pression totale pour en déduire ensuite les pressions partielles. N'oubliez pas que les valeurs données sont toujours arrondies à une ou deux décimales après la virgule pour les rendre plus lisibles. Si vous faites vous-même les calculs à la calculatrice sans jamais rien arrondir, vous verrez que l'écart entre les résultats des deux méthodes devient infime ou même nul.

Avertissements

Lorsque l'on fait de la plongée sous-marine, connaitre les pressions partielles peut devenir une question de vie ou de mort. Une pression partielle d'oxygène trop faible peut provoquer des évanouissements ou même la mort et des pressions partielles d'azote ou d'oxygène trop élevées risquent également d'intoxiquer le plongeur ^{[13]
X
Source de recherche}.