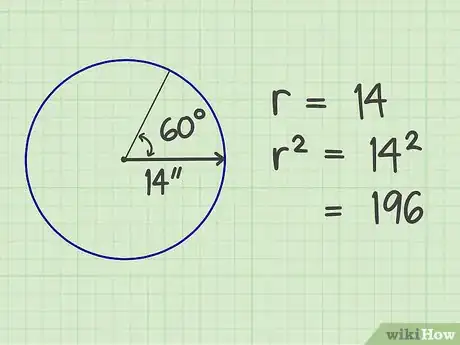Comment calculer la surface d'une forme géométrique

Coécrit par David Jia

Dans la vie, à de nombreuses reprises, vous serez amené à calculer des surfaces, parfois très différentes les unes des autres. Ainsi, si vous êtes un élève, on vous demandera de faire des exercices de calcul de surfaces, devenu adulte, vous allez devoir calculer la surface d'un mur d'une pièce afin d'acheter les pots de peinture nécessaires à sa réfection.

Méthode 1

Méthode 1 sur 7:
Calculer la surface d'un carré, d'un rectangle et d'un parallélogramme

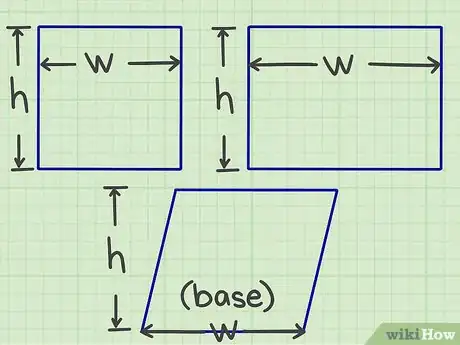
1
Mesurez la longueur et la largeur d'une de ces figures. Pour pouvoir calculer la surface de ces trois figures, il faut toujours connaître leurs longueurs et leurs largeurs (soit la mesure de deux côtés adjacents).
- Pour un parallélogramme, il faut connaître ce qu'on appelle la « base » et la hauteur, ce qui est l'équivalent de la longueur et la largeur pour les formes à angles droits.
- À l'école, ces mesures vous sont données par votre professeur. Dans la vie réelle, il faudra que vous preniez vous-même les mesures.
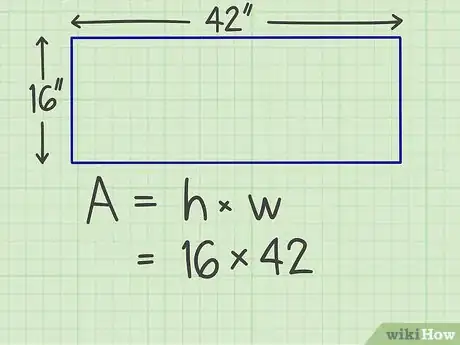
2
Multipliez les longueurs des côtés adjacents. Ainsi, si vous avez un rectangle de 16 cm de large par 42 cm de long, il faudra multiplier 16 par 42 (16 × 42).
- Dans le cas d'un carré (4 côtés égaux), c'est encore plus simple, il suffit de multiplier la longueur d'un côté par lui-même (élévation au carré). Sur une calculatrice, il y a une fonction pour élever au carré. Par exemple, vous avez une pièce carrée de 4 m de côté : vous entrez 4 sur votre machine, vous appuyez sur la touche d'élévation au carré et vous avez votre résultat.
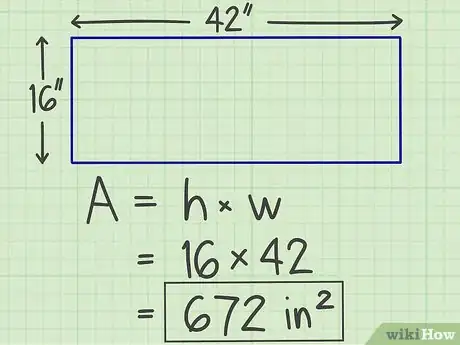
3
Faites les calculs afin d'obtenir la surface. La multiplication des deux côtés vous donne directement la surface. Attention ! Une surface se donne en « unités carrées ». Si l'on reprend l'exemple du rectangle ci-dessus (16 × 42), on obtient une surface de 672 centimètres carrés.
- L'unité « centimètres carrés » peut aussi s'écrire « cm² ».
Publicité

Méthode 2

Méthode 2 sur 7:
Calculer la surface d'un trapèze

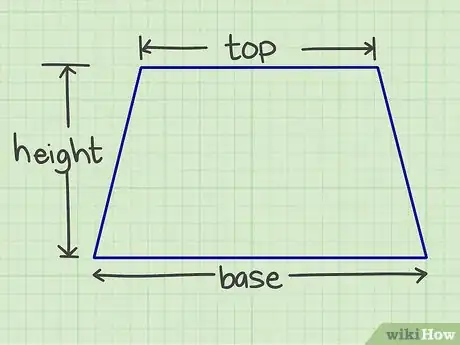
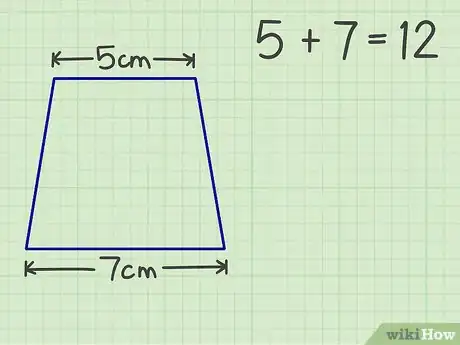
1
Prenez les mesures de votre forme. Pour votre calcul, vous allez avoir besoin des deux bases (du bas et du haut) et de la hauteur. Les deux bases sont parallèles et la hauteur est la distance à angle droit entre ces deux bases.
- À l'école, ces mesures vous sont données par votre professeur. Dans la vie réelle, il faudra que vous preniez vous-même les mesures.
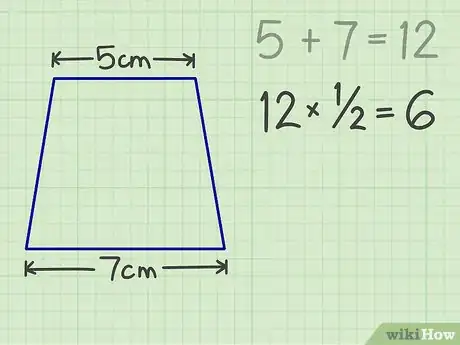
2
Additionnez les deux bases. Prenons l'exemple d'un trapèze dont la base du haut est de 5 cm et celle du bas est de 7 cm. La somme des deux donne : 5 + 7 = 12 cm.
3
Multipliez ce résultat par 1/2. On obtient : 6 (12 / 2 = 6).
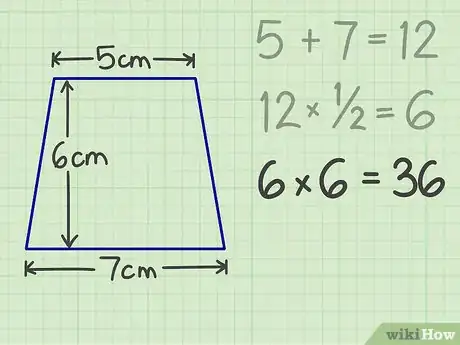
4
Multipliez ce résultat par la hauteur. Notre trapèze a, disons, une hauteur de 6 cm. On obtient : 6 × 6 = 36.
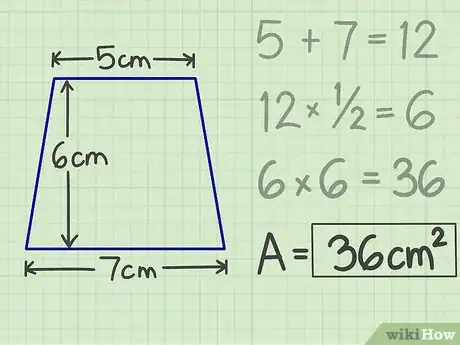
5
Présentez votre résultat. Après tous ces calculs, vous avez la surface de votre trapèze (b1 = 5 cm, b2 = 7 cm, h = 7 cm), soit 5 × 7 × 7 = 36 cm².

Publicité

Méthode 3

Méthode 3 sur 7:
Calculer la surface d'un cercle

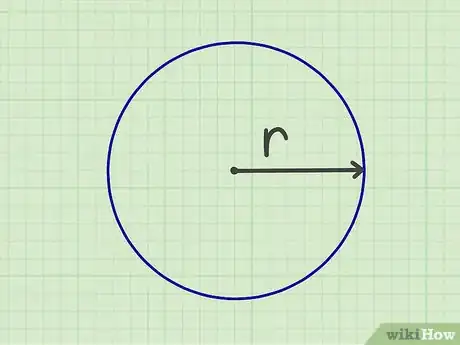
1
Déterminez le rayon (r) du cercle. Cette mesure est obligatoire si vous voulez obtenir la surface d'un cercle. Le rayon est le segment de droite qui part du centre du cercle et rejoint n'importe quel point du périmètre du cercle. On peut aussi mesurer la distance entre deux points opposés du cercle (en passant par le centre !), on obtient alors le diamètre du cercle, lequel est le double du rayon. Si vous avez le diamètre, divisez-le par 2 et vous aurez le rayon.
- À l'école, ces mesures vous sont données par votre professeur. Dans la vie réelle, il faudra que vous preniez vous-même les mesures.
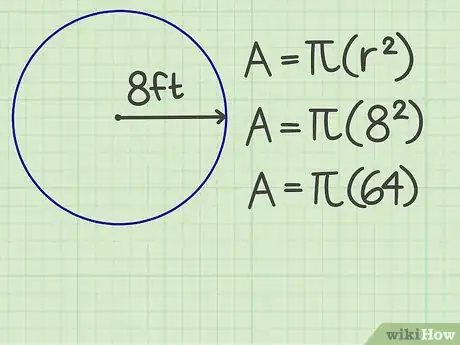
2
Élevez ce rayon au carré. Dit autrement, multipliez ce rayon par lui-même. Soit un cercle de 8 cm de rayon. Élevé au carré, on obtient 64.
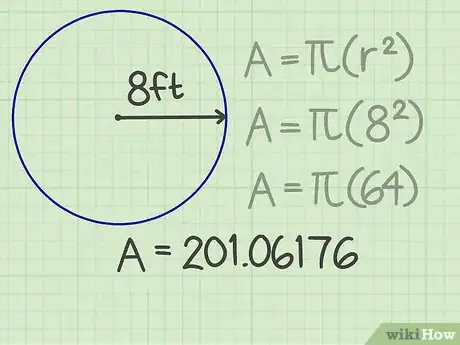
3
Multipliez par « pi ». Cette constante (π) entre dans de nombreuses formules de calculs. Si vous avez une calculatrice, il vous suffit d'appuyer sur la touche « pi » pour avoir sa valeur exacte. Sinon, vous pouvez multiplier par une valeur arrondie, comme 3,14 ou 3,14159. Avec la valeur exacte, pour notre exemple, on obtient le nombre de 201,06176.
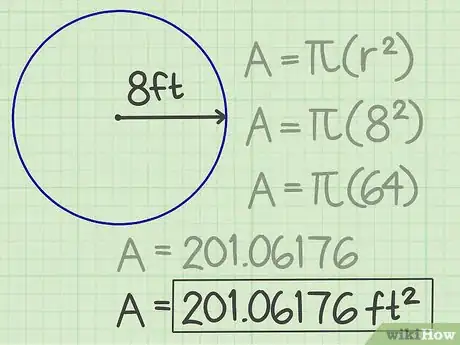
4
Présentez votre résultat. Ce dernier est tout simplement la surface de votre cercle, soit 201,06176. Il ne reste plus qu'à ajouter l'unité : le cercle a une surface de 201,06176 cm².

Publicité

Méthode 4

Méthode 4 sur 7:
Calculer la surface du secteur d'un cercle

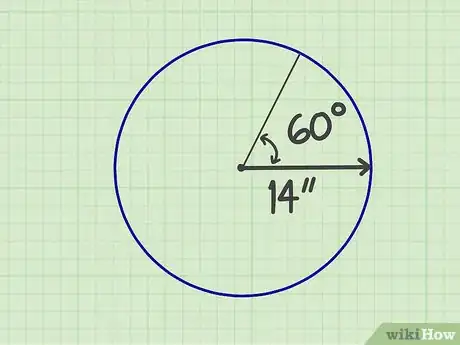
1
Prenez les mesures de votre secteur. Un secteur est une partie de cercle qui ressemble un peu aux pales d'un ventilateur ou à une part de pizza ! Pour le calcul de l'aire d'un secteur, il faut connaître le rayon du cercle en question (ou la longueur de votre « pale ») et l'angle d'ouverture de votre secteur. Prenons l'exemple d'un cercle qui fait 14 cm de rayon avec un secteur ayant un angle de 60°.
- À l'école, ces mesures vous sont données par votre professeur. Dans la vie réelle, il faudra que vous preniez vous-même les mesures.
2
Élevez ce rayon au carré. Dit autrement, multipliez ce rayon par lui-même. On obtient : 196 (14 x 14).
3
Multipliez par « pi ». Cette constante (π) entre dans de nombreuses formules de calculs. Si vous avez une calculatrice, il vous suffit d'appuyer sur la touche « pi » pour avoir sa valeur exacte. Sinon, vous pouvez multiplier par une valeur arrondie, comme 3,14 ou 3,14159. Avec la valeur exacte, pour notre exemple, on obtient le nombre de 615,75164.
4
Divisez l'angle de votre secteur par 360. On doit établir la part que représente votre secteur dans l'ensemble du cercle, on divise donc 60 par 360 (nombre de degrés d'un cercle entier). Ici, on obtient quelque chose comme 0,166… Le résultat est un nombre décimal de période 6. On arrondit donc à 0,166 pour faciliter les calculs. Dit autrement, ce secteur représente 16,66 % du cercle entier.
5
Multipliez ce dernier résultat par la surface du cercle calculée plus haut. On doit faire le calcul suivant : 0,166 × 615,75164, ce qui nous donne au final : 102,214.
6
Présentez votre résultat. Ce dernier est tout simplement la surface de votre secteur, soit 102,214 cm².

Publicité

Méthode 5

Méthode 5 sur 7:
Calculer la surface d'une ellipse

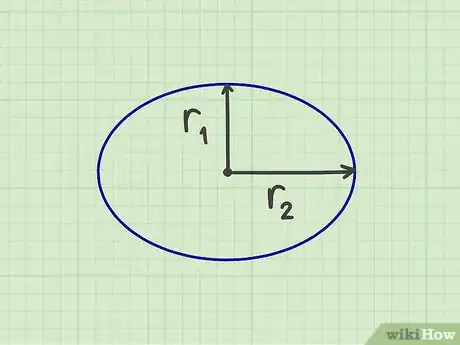
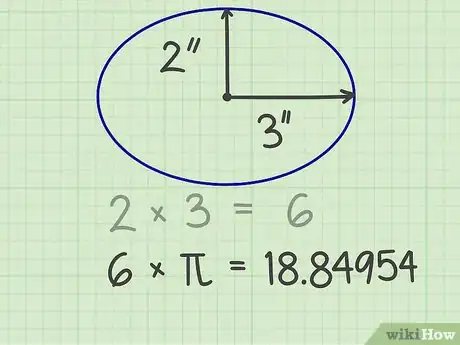
1
Prenez les mesures de votre ellipse. Pour calculer l'aire d'une telle figure, il vous faut avoir les « deux rayons » (le grand et le petit). Ils sont en quelque sorte la largeur et la hauteur de l'ellipse. Ils s'obtiennent en divisant par 2 la largeur de l'ellipse (grand rayon) et la hauteur (petit rayon). On parle de rayon, car on part chaque fois du centre de l'ellipse. Ces deux rayons forment entre eux un angle droit.
- À l'école, ces mesures vous sont données par votre professeur. Dans la vie réelle, il faudra que vous preniez vous-même les mesures.
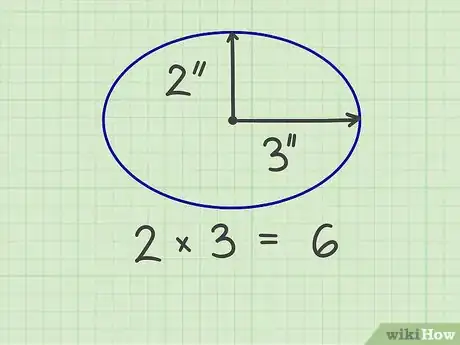
2
Multipliez les deux rayons. Prenons le cas d'une ellipse qui a 6 cm de large par 4 de haut. Cela nous donne deux rayons : l'un de 3 cm, l'autre de 2 cm. On les multiplie et on obtient : 3 × 2 = 6.
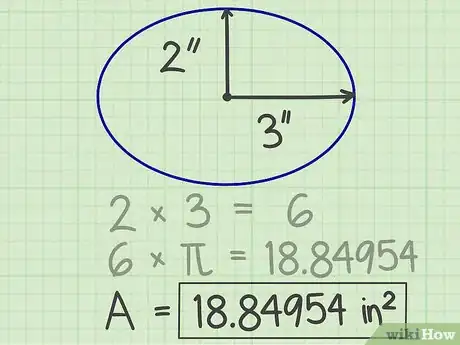
3
Multipliez ce résultat par « pi ». Cette constante (π) entre dans de nombreuses formules de calculs. Si vous avez une calculatrice, il vous suffit d'appuyer sur la touche « pi » pour avoir sa valeur exacte. Sinon, vous pouvez multiplier par une valeur arrondie, comme 3,14 ou 3,14159. Avec la valeur exacte, pour notre exemple, vous obtiendrez le nombre de 18,84954.
4
Présentez votre résultat. Ce dernier est tout simplement la surface de votre ellipse. La surface de notre figure elliptique est donc de 18,84954 cm.²

Publicité

Méthode 6

Méthode 6 sur 7:
Calculer la surface d'un triangle

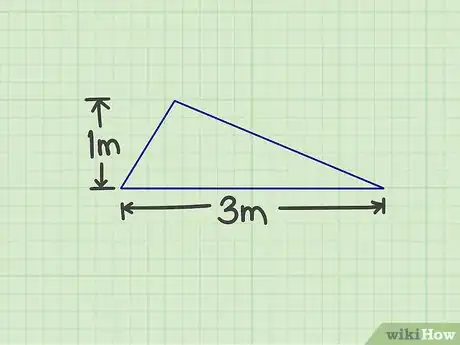
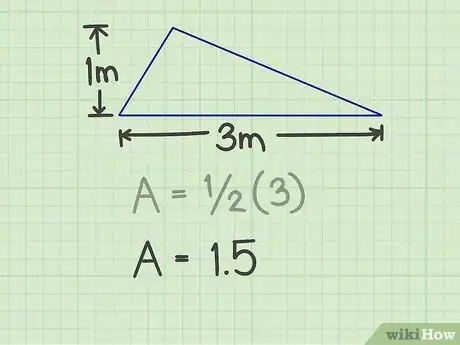
1
Prenez les mesures de votre triangle. Il vous faut deux mesures : la longueur de la base et la hauteur du triangle. Pour la base, vos pouvez prendre n'importe quel côté. Quant à la hauteur, il faut prendre celle liée à cette base. Prenons l'exemple d'un triangle de 3 mètres de base pour une hauteur de 1 mètre.
- À l'école, ces mesures vous sont données par votre professeur. Dans la vie réelle, il faudra que vous preniez vous-même les mesures.
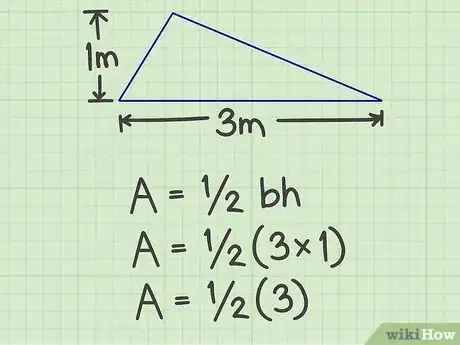
2
Multipliez la base par la hauteur. Ici, on obtient : 3 × 1 = 3.
3
Multipliez ce résultat par 1/2. On obtient : 1,5.
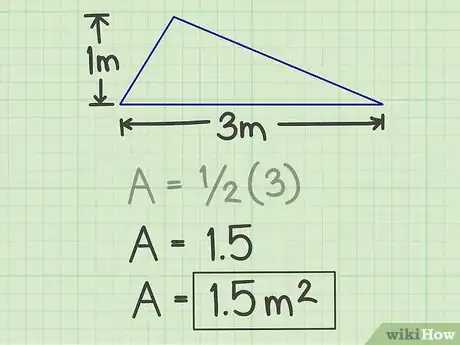
4
Présentez votre résultat. Ce dernier est tout simplement la surface de votre triangle, soit 1,5 m²

Publicité

Méthode 7

Méthode 7 sur 7:
Calculer la surface d'une forme complexe

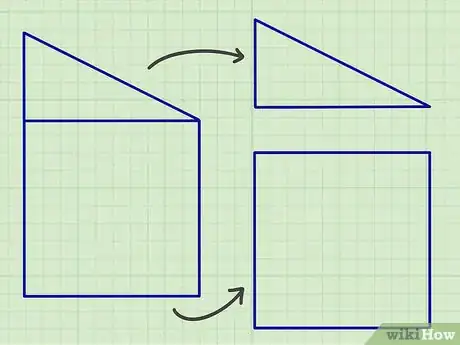
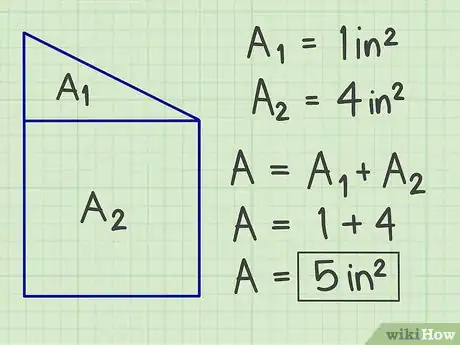
1
Subdivisez votre forme en formes géométriques simples. Si vous avez une surface tarabiscotée à calculer, essayez de la décomposer en formes élémentaires, telles celles que l'on a évoquées précédemment. Dans un problème scolaire, avec un plan de la figure, ce sera assez simple. Dans la vie de tous les jours, il serait bon de dresser sur papier le plan de votre surface afin de pouvoir la décomposer correctement.
- Il faut commencer par repérer les angles droits (s'il y en a !) et les lignes parallèles. Ces deux éléments sont à l'origine de nombreuses formes géométriques simples.
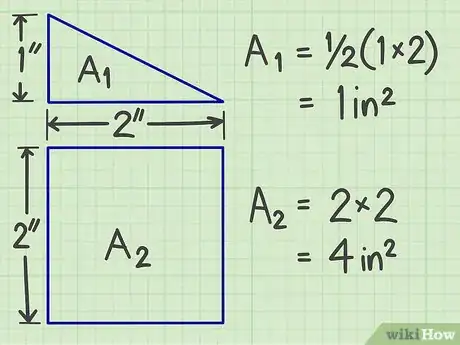
2
Calculez les surfaces de chacune de ces formes simples. En fonction des formes simples que vous avez déterminées, reportez-vous aux parties correspondantes de cet article.
3
Additionnez toutes les surfaces que vous avez trouvées. Vous obtiendrez la surface totale de votre figure de départ.
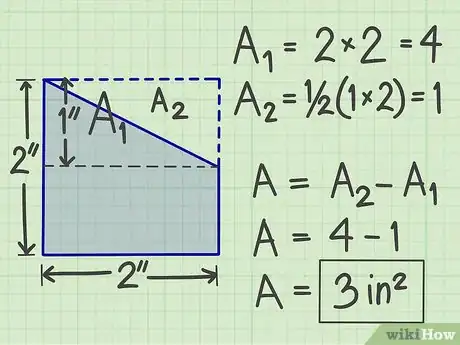
4
Il existe d'autres approches de calcul, en fonction de la forme que vous avez. L'une d'entre elles consiste à ajouter une surface à votre figure pour que l'ensemble forme une figure simple. Vous calculez l'aire de cette figure, puis vous retranchez la surface de la figure que vous avez ajoutée.

Publicité

Conseils

Utilisez cette calculatrice en ligne pour vous aider ou vous permettre de comprendre comment on fait.
N'hésitez pas à demander de l'aide à un ami si vous rencontrez des difficultés !

Avertissements

Vérifiez toujours vos calculs !
Faites attention à bien prendre les mesures et surtout à avoir les mêmes unités. Ne mélangez pas des mètres et des centimètres.