Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 49 310 fois.
L’aire totale de la surface d'un cône est obtenue en additionnant l'aire de la surface latérale et l’aire de la surface de la base. Si vous connaissez la longueur du rayon de la base et celle de la génératrice du cône, il est très facile de la calculer avec une formule toute simple. Dans d’autres exercices, on pourra vous donner le rayon et la hauteur du cône, ou le rayon et le volume du cône. Dans le premier cas, il faudra en passer par le théorème de Pythagore, dans le second cas, il existe une formule toute faite qui permet de trouver la génératrice, et par la suite l'aire de surface totale.
Étapes
Méthode 1
Méthode 1 sur 3:Calculer l'aire totale de la surface d'un cône en ayant le rayon et la génératrice
-
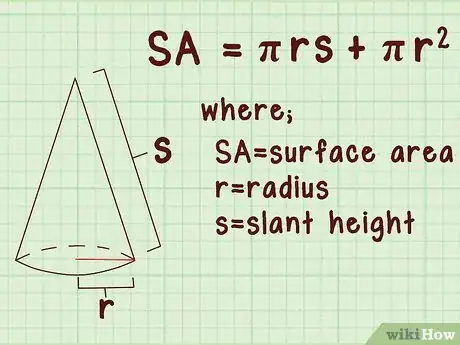
1Posez la formule de l'aire totale de surface du cône. La formule est la suivante : , étant l’aire totale de surface du cône, , la longueur du rayon de la base du cône, et représentant la génératrice, ou apothème, du cône [1] .
- L’aire totale de la surface d'un cône est égale à la somme de l’aire de la surface latérale, soit , et de l'aire de la base, à savoir , étant donné que la base d'un cône est un cercle.
- La génératrice, aussi appelée « apothème », est le segment qui relie le sommet à n’importe quel point du cercle de la base du cône [2] .
- Faites attention à ne pas confondre la génératrice et la hauteur, cette dernière étant la longueur de la perpendiculaire abaissée du sommet sur la base [3] .
-
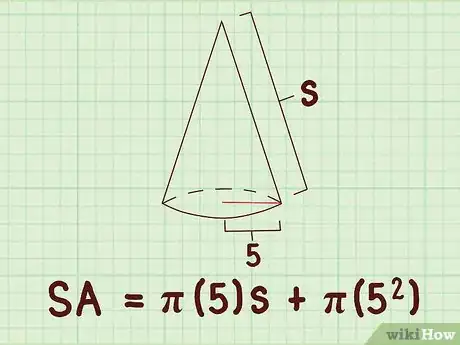
2Faites l'application numérique. Dans la formule, remplacez par la valeur réelle du rayon. Cette longueur est soit donnée soit mesurée directement sur le croquis. Faites attention ! Le rayon apparait à deux reprises dans la formule.
- Ainsi, si le rayon de la base d'un cône est de 5 cm, votre formule sera la suivante :
-
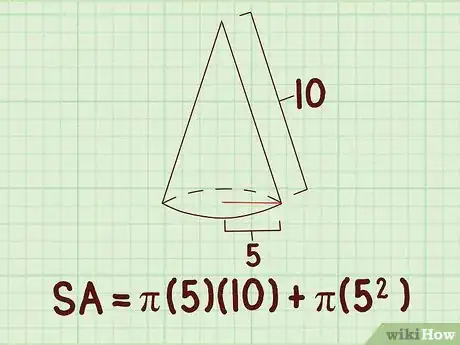
3Dans la formule, mettez la valeur réelle de la génératrice. Cette longueur est soit donnée soit mesurée directement sur le croquis.
- Ainsi, si la génératrice d'un cône est de 10 cm, votre formule sera la suivante :
-
4Calculez l’aire de la surface latérale du cône. La formule est donc : . Pour cela, multipliez le rayon par la génératrice et par . Si vous faites les calculs à la main, prenez 3,14 comme valeur approchée de .
- Reprenons l'exemple :
- Reprenons l'exemple :
-
5Calculez l'aire de la base du cône. La formule est la suivante : . Pour cela, élevez au carré le rayon de la base, puis multipliez par . Si vous faites les calculs à la main, prenez 3,14 comme valeur approchée de .
- Reprenons l'exemple :
- Reprenons l'exemple :
-
6Additionnez tout. Additionnez l’aire de la surface latérale et celle de la base du cône. Vous obtenez alors l’aire totale de surface du cône, en unités carrées.
- Reprenons l'exemple :
Ainsi, l’aire totale de la surface d'un cône ayant 5 cm de rayon et une génératrice de 10 cm est de 235,5 cm2.
Publicité - Reprenons l'exemple :
Méthode 2
Méthode 2 sur 3:Calculer l'aire totale de la surface d'un cône en ayant le rayon et la hauteur
-
1Posez la formule du théorème de Pythagore. La formule est la suivante : . Dans cette formule, et sont les longueurs des deux côtés adjacents à l’angle droit, et , la longueur de l’hypoténuse (le côté opposé à l'angle droit) [4] .
-
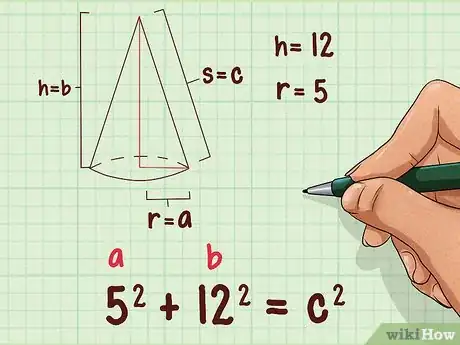
2Faites l’application numérique. Remplacez le rayon de la base et la hauteur par leurs vraies valeurs. Le rayon de la base et la hauteur du cône seront les deux côtés adjacents du triangle rectangle. On posera que le rayon est la variable de la formule de Pythagore, et la hauteur , la variable de cette même formule.
- Ainsi, si le rayon de base de votre cône est de 5 cm et la hauteur, de 12 cm, votre formule sera la suivante :
-
3Faites les calculs. Élevez le rayon au carré, faites de même avec la hauteur, puis additionnez les deux résultats. Rappelons au passage qu’élever un nombre au carré revient à le multiplier par lui-même.
- Reprenons l'exemple :
- Reprenons l'exemple :
-
4Extrayez la racine carrée de chaque membre de la formule. Vous obtiendrez alors la longueur de l’hypoténuse du triangle rectangle qui vous intéresse ici, car c’est aussi la génératrice du cône [7] .
- Reprenons l'exemple :
Ainsi, la génératrice du cône est de 13 cm.
- Reprenons l'exemple :
-
5Posez la formule de l'aire totale de surface du cône. La formule est la suivante : , étant l'aire totale de surface du cône, , le rayon de la base du cône, et représentant la génératrice, ou l'apothème, du cône [8] .
- L’aire totale de la surface d'un cône s’obtient en additionnant l'aire de la surface latérale, soit , et l'aire de la base, à savoir , étant donné que la base d'un cône est un cercle.
-
6Remplacez les valeurs littérales par leurs valeurs réelles. Le rayon de la base est en général donné et vous avez déjà la longueur de la génératrice. Faites très attention à bien prendre la génératrice, et non pas la hauteur. Si vous faites les calculs à la main, prenez 3,14 comme valeur approchée de .
- Ainsi, pour un cône avec un rayon de base de 5 cm et une génératrice de 13 cm, votre formule sera la suivante :
-
7Faites toutes les opérations. Respectez l'ordre des opérations : d'abord les puissances, puis les produits, enfin les sommes. Multipliez pour trouver l’aire latérale, faites de même pour l'aire de la base. Pour finir, faites l’addition des deux. Vous obtenez alors l’aire totale de surface du cône en unités carrées.
- Reprenons l'exemple :
Ainsi, l'aire totale de la surface d'un cône dont la base a 5 cm de rayon et dont la hauteur est de 12 cm, cette aire est donc de 282,6 cm2.
Publicité - Reprenons l'exemple :
Méthode 3
Méthode 3 sur 3:Calculer l'aire totale de la surface d'un cône en ayant le rayon et le volume
-
1Posez la formule du volume d'un cône. La formule est la suivante : , étant le volume du cône, , le rayon de la base du cône, et représentant la hauteur (perpendiculaire) du cône [9] .
-
2Remplacez les valeurs littérales par leurs valeurs réelles. On devrait vous donner le volume et la longueur du rayon. Si ce n’est pas le cas, vous ne pourrez rien faire. Si vous faites les calculs à la main, prenez 3,14 comme valeur approchée de .
- Admettons que vous ayez un cône dont le volume est de 950 cm3 et dont le rayon de la base est de 6 cm, votre formule sera la suivante :
-
3Faites les opérations. Commencez par élever au carré le rayon, puis multipliez ce résultat par . Enfin, multipliez ce résultat par . Il ne vous restera alors plus que la variable et son coefficient.
- Reprenons l'exemple :
- Reprenons l'exemple :
-
4Divisez par le coefficient de . En divisant chaque membre de l'égalité par le coefficient de , vous obtiendrez la valeur de , qui est en fait la hauteur du cône. Cette dernière va vous servir à calculer la génératrice du cône, qui, à son tour, servira à calculer l'aire de surface.
- Reprenons l'exemple en intervertissant les membres de l'égalité :
Ainsi, la hauteur du cône est de 25,21 cm.
- Reprenons l'exemple en intervertissant les membres de l'égalité :
-
5Posez la formule du théorème de Pythagore. La formule est la suivante : . Dans cette formule, et sont les longueurs des deux côtés adjacents à l’angle droit, et , la longueur de l’hypoténuse (le côté opposé à l'angle droit) [12] .
-
6Faites l’application numérique. Remplacez le rayon de la base et la hauteur par leurs vraies valeurs. Le rayon de la base et la hauteur du cône seront les deux côtés adjacents du triangle rectangle. On posera que le rayon est la variable de la formule de Pythagore, et la hauteur , la variable de cette même formule.
- Ainsi, si le rayon d'un cône est de 6 cm et sa hauteur, de 25,21 cm, votre formule sera la suivante :
-
7Trouvez . Vous obtiendrez alors la longueur de l’hypoténuse du triangle rectangle qui vous intéresse ici, car c’est aussi la génératrice du cône.
- Reprenons l'exemple :
Ainsi, la génératrice du cône est de 25,91 cm.
- Reprenons l'exemple :
-
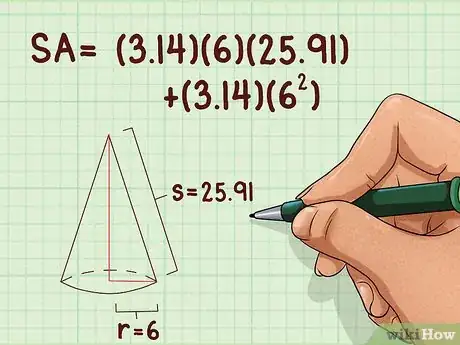
8Posez la formule de l'aire totale de surface du cône. La formule est la suivante : , étant l'aire totale de surface du cône, , le rayon de la base du cône, et représentant la génératrice, ou apothème, du cône [13] .
- L’aire totale de la surface d'un cône s’obtient en additionnant l'aire de la surface latérale, soit , et l'aire de la base, à savoir , étant donné que la base d'un cône est un cercle.
-
9Remplacez les valeurs littérales par leurs valeurs réelles. Faites très attention à bien prendre la génératrice, et non pas la hauteur. Si vous faites les calculs à la main, prenez 3,14 comme valeur approchée de .
- Ainsi, pour un cône d’un rayon de base de 6 cm et une génératrice de 25,91 cm, votre formule sera la suivante :
-
10Faites toutes les opérations. Respectez l'ordre des opérations : d'abord les puissances, puis les produits, enfin les sommes. Multipliez pour trouver l’aire latérale, faites de même pour l'aire de la base. Pour finir, faites l’addition des deux. Vous obtenez alors l’aire totale de surface du cône en unités carrées.
- Reprenons l'exemple :
Ainsi, l'aire totale de la surface d'un cône ayant un rayon de base de 6 cm et un volume de 950 cm3 est de 601,18 cm2.
Publicité - Reprenons l'exemple :
Conseils
- Le théorème de Pythagore s’applique au triangle formé par le rayon de la base, la hauteur, et la génératrice du cône, la génératrice étant ici l’hypoténuse : (génératrice)2 = (rayon)2 + (hauteur)2
Références
- ↑ http://www.mathopenref.com/conearea.html
- ↑ http://www.mathwords.com/s/slant_height.htm
- ↑ http://www.mathopenref.com/cone.html
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathwords.com/s/slant_height.htm
- ↑ http://www.mathopenref.com/cone.html
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_VolumeSurfaceAreaCones.xml
- ↑ http://www.mathopenref.com/conearea.html
- ↑ http://www.mathopenref.com/conevolume.html








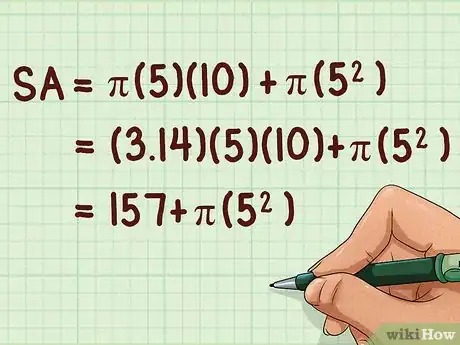








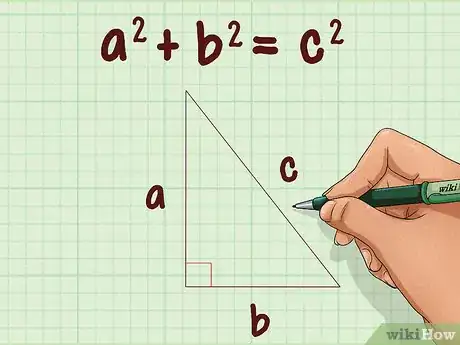






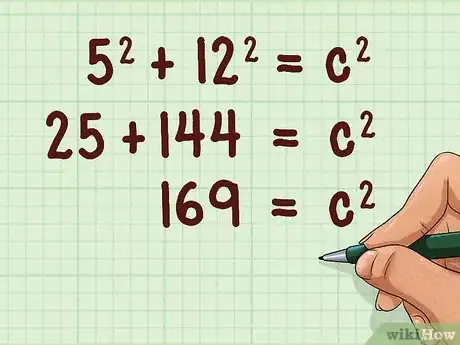


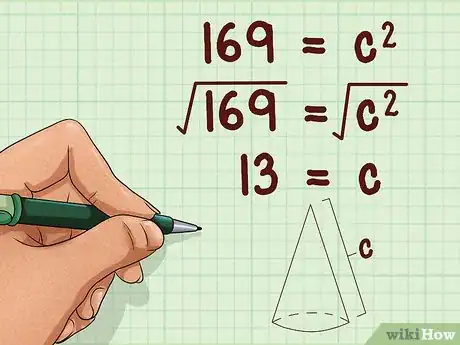





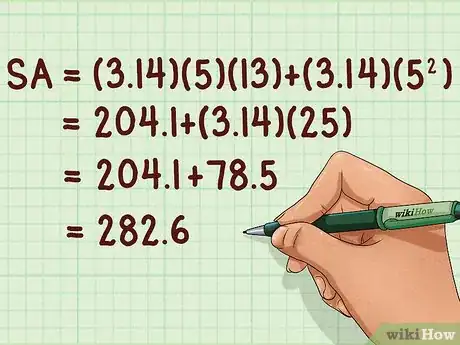






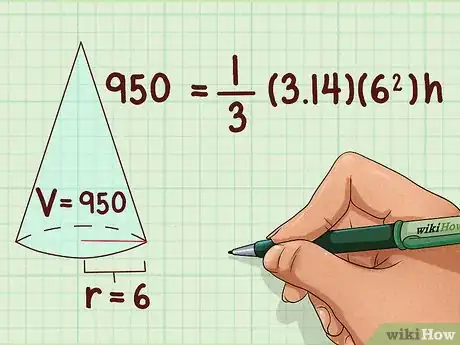










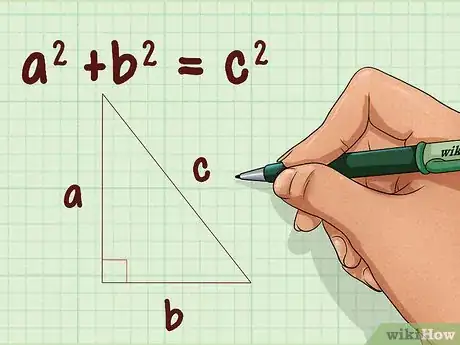
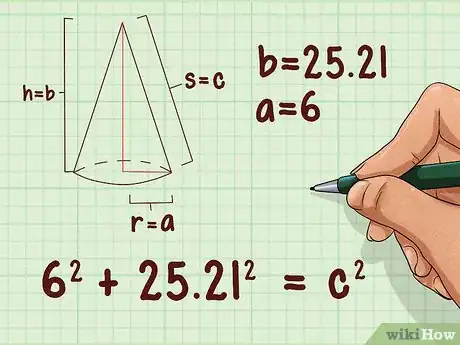

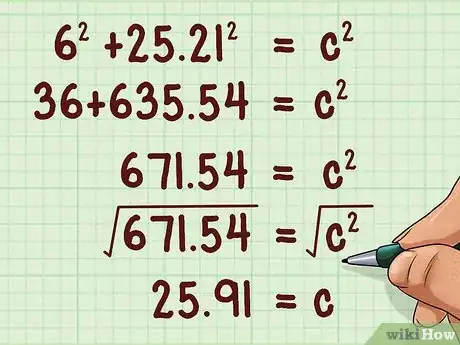






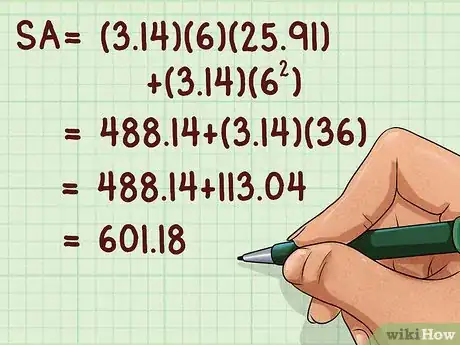






















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 49 310 fois.