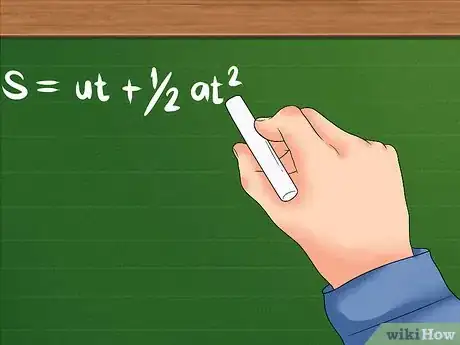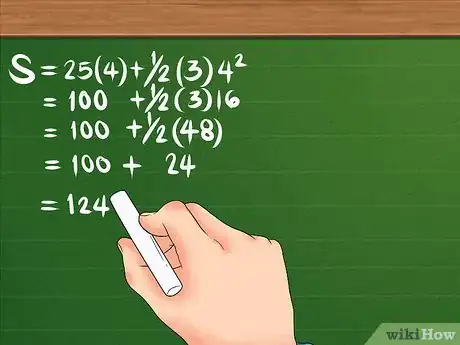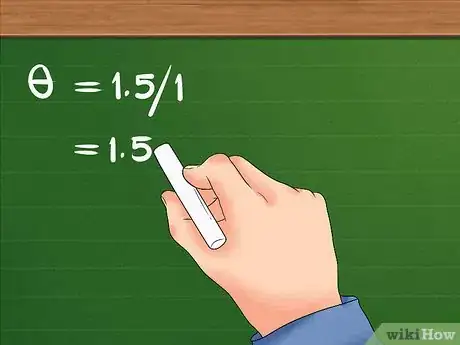Comment calculer le déplacement

En physique, le déplacement est le changement de position d'un objet dans l'espace. Quand on calcule un déplacement, on cherche à savoir de combien « s'est déplacé » un objet entre son point de départ et son point d'arrivée, indépendamment du chemin emprunté. La formule de calcul du déplacement varie en fonction des données qui vous ont été fournies dans l'exercice. Nous voyons ces différents cas de figure dans l'article qui suit.

Partie 1

Partie 1 sur 5:
Calculer le déplacement résultant

1
Utilisez la formule du déplacement résultant lorsqu'on vous donne les distances parcourues entre un point de départ et un point d'arrivée. Entre deux points, la distance n'est pas le déplacement, dans la mesure où le déplacement résultant représente le nombre de « pieds » ou de « mètres » qui ont été parcourus par un objet. C'est grâce à ces distances intermédiaires que vous allez pouvoir calculer le déplacement ou, si vous préférez, la distance qui sépare le point de départ de l'objet de son point d'arrivée.
- La formule du déplacement résultant est la suivante : d = √x²+y² avec « d » représentant le déplacement, « x » est la première direction empruntée par l'objet et « y » est la seconde direction empruntée par le même objet ^{[1]
  X
  Source de recherche}. Si l'objet ne suit qu'une direction, alors y= 0.
- Un objet ne peut suivre que deux directions, étant donné que les directions nord/sud se font sur le même axe, de même pour les directions est/ouest. On parle de « mouvements neutres ».
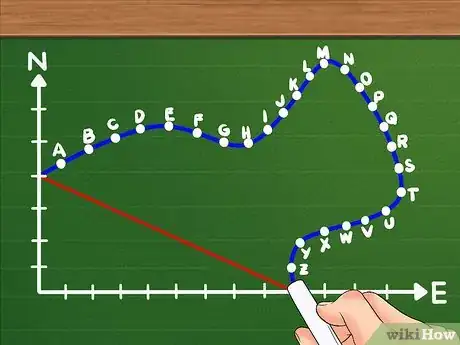
2
Reliez les points d'étape du cheminement de l'objet en les nommant dans l'ordre de A à Z. Reliez ces points par une ligne droite à l'aide d'une règle.
- Pour finir, n'oubliez pas de relier par une ligne droite le point de départ. Cette droite représente le déplacement que nous nous imposons de trouver.
- Prenons l'exemple d'un objet qui parcourt 300 mètres vers l'est, puis, 400 mètres vers le nord, On a alors un parcours qui forme un triangle rectangle ABC. AB sera un des côtés (200 m), BC sera le deuxième côté (400 m). AC formera alors l'hypoténuse du triangle et sa longueur constituera le déplacement de l'objet. Les deux directions sont ici « l'est » et « le nord ».
3
Remplacez x et y par leurs valeurs respectives afin de calculer x² et y². Les deux directions empruntées par l'objet ayant été définies, vous pouvez faire l'application numérique..
- Par exemple, x = 300 et y = 400. La formule devient alors : d = √300² + 400².
4
Faites les calculs en respectant l'ordre des opérations. Faites 300 au carré, puis 400 au carré. Additionnez les deux résultats et prenez la racine carrée de cette somme.
- Par exemple : d = √90000 + 160000 = √250000 = 500. Le déplacement est donc de 500 mètres.
Publicité

Partie 2

Partie 2 sur 5:
Quand les valeurs de la vitesse et du temps sont données

1
Utilisez cette formule quand, dans le problème, on vous donne la vitesse de l'objet et la durée du déplacement. Dans certains exercices, on ne vous donnera pas la distance, mais la vitesse de l'objet en déplacement et la durée de ce déplacement. À l'aide de ces deux valeurs, vous allez pouvoir calculer la distance parcourue.
- En ce cas, la formule sera : d = 1/2(v_i + v_f)t avec v_i = vitesse initiale de l'objet, c'est-à-dire la vitesse qu'il avait au départ, v_f = vitesse finale de l'objet, c'est-à-dire la vitesse qu'il avait à l'arrivée et t = temps mis par l'objet pour se déplacer entre les deux points.
- Par exemple : une voiture se déplace sur une route pendant 45 secondes (temps mis). Disons qu'elle se dirige vers l'ouest à une vitesse de 20 m/s (vitesse initiale) et, arrivée au bout de sa course, elle a une vitesse de 23 m/s (vitesse finale) ^{[2]
  X
  Source de recherche}. Question : calculez le déplacement à partir de ces données.
2
Faites l'application numérique en entrant dans la formule les vitesses et le temps mis. Maintenant que vous avez la durée de déplacement du véhicule, sa vitesse initiale et sa vitesse finale, vous êtes en mesure de calculer la distance parcourue.
- En appliquant les données du problème, la formule devient : d = 1/2(20 + 23)(45).
3
Faites tous les calculs après avoir remplacé les variables de la formule par leurs valeurs. N'oubliez pas de respecter l'ordre des opérations, sinon vous trouverez une valeur de déplacement erronée !
- Avec cette formule, le sens des vitesses initiale et finale importe peu étant donné qu'elles sont additionnées, puisque v_i + v_f = v_f + v_i. Par contre, dans d'autres formules, vous ne pourrez vous permettre d'invertir les deux, sous peine d'obtenir un résultat faux.
- La formule devient alors : d = 1/2(43)45. Commencez par diviser 43 par 2, ce qui donne : 21,5. Multipliez ensuite 21,5 par 45, soit 967,5 mètres. Ce nombre de 967,5 représente le déplacement, c'est-à-dire la distance entre le point de départ et le point d'arrivée de la voiture.
Publicité

Partie 3

Partie 3 sur 5:
Quand les valeurs de la vitesse initiale, de l'accélération et de la durée sont données

1
Vous devez utiliser une autre formule de calcul si on vous donne la vitesse initiale, l'accélération et la durée. Certains exercices ne vous donnent que la vitesse à laquelle se déplace l'objet, dans quelle proportion il accélère et la durée du parcours. Vous devez en ce cas utiliser une formule modifiée.
- Elle se présente ainsi : d = v_it + 1/2at² avec « v_i » représentant toujours la vitesse initiale, « a » est l'accélération de l'objet (modification affectant la vitesse de l'objet) et « t » représente la durée de l'accélération. Cette dernière variable est donnée dans diverses unités de temps (secondes, minutes, heures…)
- Prenons une voiture roulant à 25 m/s (vitesse initiale) et qui accélère de 3 m/s2 (accélération) pendant 4 secondes (temps). Question : calculez le déplacement de la voiture au bout des 4 secondes ^{[3]
  X
  Source de recherche} ?
2
Faites l'application numérique après avoir remplacé les variables de la formule par leurs valeurs. À la différence de la formule précédente, on n'a besoin ici que de la vitesse initiale. Aussi faudra-t-il faire attention à mettre la bonne valeur !
- Reprenons les valeurs de l'exemple et mettons-les dans la formule. On obtient alors : d = 25(4) + 1/2(3)4². Il est ici pratique de mettre des parenthèses autour de l'accélération et de la durée pour ne pas commettre d'erreurs.
3
Faites ensuite les calculs en respectant l'ordre des opérations. Il existe un mot mnémotechnique pour se souvenir de cet ordre ; c'est PEMDAS (Parenthèses, Exposants, Multiplication, Division, Addition et Soustraction.
- Reprenons l'application numérique : d = 25(4) + 1/2(3)4². Commencez par élever 4 au carré, ce qui donne 16. Multipliez ensuite 16 par 3, on obtient 48. Multipliez 25 par 4, ce qui donne 100. Divisez 48 par 2 pour obtenir 24. La formule se résume désormais à : d = 100 + 24. On additionne le tout. Au final, le déplacement a été de 124 mètres ^{[4]
  X
  Source de recherche}.
Publicité

Partie 4

Partie 4 sur 5:
Calculer un déplacement angulaire

1
Trouvez le déplacement angulaire d'un objet qui se déplace le long d'une trajectoire courbe. On a vu comment calculer le déplacement selon une trajectoire rectiligne. Il en va un peu différemment si l'objet suit une trajectoire courbe.
- Pensez à une jeune fille installée sur un carrousel. En tournant, elle décrit un parcours courbe. Le déplacement angulaire mesure en fait la distance la plus courte entre le point de départ et celui d'arrivée, dans le cas où un objet ne suit pas un parcours rectiligne.
- La formule du déplacement angulaire est la suivante : θ = S/r, dans laquelle « θ » représente le déplacement angulaire, « S » est le déplacement linéaire et « r », le rayon. Par déplacement linéaire, on entend la distance réellement parcourue par l'objet dans sa rotation. Le rayon est la distance qui va de l'objet au centre du cercle. Nous devons rechercher le déplacement angulaire.
2
Dans la formule, remplacez les variables (le déplacement linéaire, le rayon) par leurs valeurs respectives. Nous vous rappelons que le rayon est la distance qui va de l'objet au centre du cercle. Ainsi, si on vous donne un exercice avec le diamètre (du carrousel, par exemple), il faudra diviser cette valeur par 2 pour avoir le rayon.
- Reprenons l'exemple de la jeune fille installée sur un des chevaux d'un carrousel. Ce dernier est à 1 mètre du centre (c'est le rayon). Si la jeune fille parcourt une distance (un arc de cercle) de 1,5 mètre (déplacement linéaire), quel est son déplacement angulaire ?
- Votre formule ressemble désormais à ceci : θ = 1,5/1.
3
Divisez le déplacement linéaire par le rayon. C'est ainsi qu'on calcule le déplacement angulaire de l'objet.
- La division de 1,5 par 1 donne 1,5. Le déplacement angulaire de la fille est donc de 1,5 radians.
- Le déplacement angulaire mesure en fait non pas une distance, mais un angle de rotation, celui qui existe entre la position de départ et celle d'arrivée. Les angles se mesurent en radians.
Publicité

Partie 5

Partie 5 sur 5:
Comprendre ce qu'est un déplacement

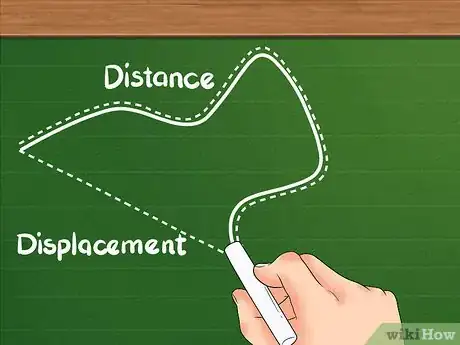
1
Vous ne devez pas confondre « distance » et « déplacement » ». La distance fait référence à la totalité du chemin réellement parcouru par un objet.
- La distance est ce qu'on appelle une« quantité scalaire ». Elle fait référence à la totalité du chemin réellement parcouru, quelles que soient les directions prises pendant le parcours ^{[5]
  X
  Source de recherche}.
- Par exemple, vous marchez 2 mètres en direction de l'est, puis 2 mètres vers le sud, encore 2 mètres vers l'ouest et enfin, 2 mètres vers le nord : vous êtes revenu à votre position originelle ! Vous avez donc bien parcouru une distance de 8 mètres, mais vous vous êtes déplacé de… 0 mètre, puisque votre point d'arrivée est également votre point de départ (votre parcours dessine un carré parfait) ^{[6]
  X
  Source de recherche}.
2
Comprenez bien que le déplacement est la distance directe entre deux points. Ce n'est pas la somme des distances qui ont pu être parcourues pour aller indirectement du point de départ à celui d'arrivée. Le déplacement est une des composantes de la surface délimitée par l'objet lors de son parcours du point de départ à celui d'arrivée.
- Le déplacement est donc une « quantité vectorielle » et prend en compte la direction de chaque étape du parcours.
- Admettons que vous parcouriez 5 mètres en direction de l'est, puis vous faites à nouveau 5 mètres en direction de l'ouest. Vous avez certes parcouru 10 mètres, mais vous êtes revenus au point de départ : votre déplacement a été de 0 mètre.
3
Ayez toujours en mémoire les mots « en avant / en arrière » quand vous travaillez sur un déplacement. Si votre objet fait deux mouvements, un en avant et un autre en arrière, le déplacement diminue, voire s'annule..
- Imaginez l'entraineur d'une équipe de football tentant de replacer ses joueurs depuis la ligne de touche. Il se déplace sans arrêt le long de cette ligne ^{[7]
  X
  Source de recherche}. Pour parler à tel ou tel joueur, il se déplace une fois à droite, une fois à gauche, puis à nouveau à droite, etc. Si, à la mi-temps, vous additionnez tous ses allers-retours, vous allez obtenir la distance qu'il a parcourue. Mais s'il se lève du banc des entraineurs, se déplace vers sa gauche et s'arrête pour aller parler à son arrière, vous pourrez mesurer, entre le banc et l'endroit où il est, ce qu'on appelle son « déplacement » ^{[8]
  X
  Source de recherche}.
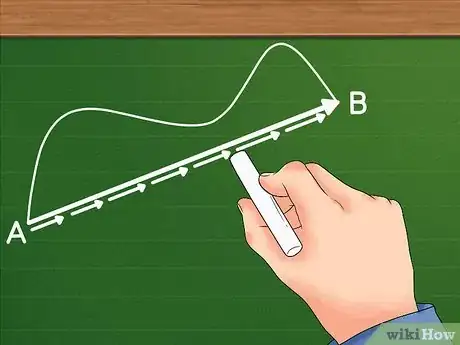
4
Un déplacement se mesure selon une ligne rectiligne, non courbe ^{[9]
X
Source de recherche}. La mesure d'un déplacement s'obtient en prenant la distance la plus courte (souvent la plus rapide !) entre deux points.
- Un trajet courbe vous mène certes de votre point de départ à votre point d'arrivée, mais ce n'est pas le trajet le plus court. Pour mieux vous faire comprendre, imaginons que vous marchiez tout droit et que vous rencontriez un gros pilier devant vous. Bien sûr, vous ne pouvez pas traverser le pilier, vous le contournez donc. Vous vous retrouvez alors au même point que si vous aviez traversé le pilier, pourtant vous avez plus marché que prévu à cause de ce pilier.
- En général, on a affaire à des déplacements en ligne droite, mais on peut aussi mesurer le déplacement d'un objet se mouvant selon une trajectoire courbe. On parle alors de « déplacement angulaire », lequel se calcule en mesurant le trajet le plus court qui va du point de départ au point d'arrivée.
5
Comprenez bien qu'un déplacement peut avoir une valeur négative, ce qui n'est pas le cas de la distance. Si votre point d'arrivée est atteint suite à un déplacement en sens opposé à celui du point de départ, alors vous vous êtes déplacé négativement. On voit bien ici que le déplacement est vectoriel.
- Admettons que vous parcouriez 5 mètres vers l'est, puis 3 mètres vers l'ouest. Vous êtes donc à 2 mètres de votre point de départ, mais, en fait, votre déplacement devrait de - 2 mètres, car vous vous êtes déplacés en sens inverse. Une distance est, par contre, toujours positive, parce qu'on ne peut pas parcourir une distance « de moins » x mètres, miles, etc.
- Un déplacement négatif ne signifie pas que le déplacement décroit, mais qu'il s'est fait en sens inverse.
6
Il peut arriver que la distance et le déplacement aient les mêmes valeurs. Ainsi, si vous marchez sur 25 mètres et que vous vous arrêtez (fin de votre parcours), distance et déplacement sont identiques, soit 25 m.
- Cette remarque n'est valable que lorsqu'on va d'un point à un autre en ligne droite ^{[10]
  X
  Source de recherche}. Admettons que vous habitiez à San Francisco (Californie) et que vous trouviez un travail à Las Vegas (Nevada). Vous allez être obligé de vous rapprocher de Las Vegas. Si vous prenez un avion qui fait directement San Francisco - Las Vegas, vous allez parcourir 671 km et vous aurez effectué un déplacement de… 671 km.
- Admettons que vous alliez toujours de San Francisco à Las Vegas, mais en voiture cette fois. Vous allez vous déplacer de 671 km, mais vous allez parcourir 906 km ^{[11]
  X
  Source de recherche}. En effet, sur la route, on n'a pas toujours un trajet direct, la route change de direction (à droite ici, à gauche là), la distance est toujours plus élevée qu'à vol d'oiseau.
Publicité

Conseils

Vous pouvez aussi utiliser cette méthode pour déterminer le déplacement de la ligne de flottaison d'un bateau. Le niveau de cette ligne est fixé par le poids du volume d'eau déplacé par la carène d'un bateau qui flotte (« poussée d'Archimède »).