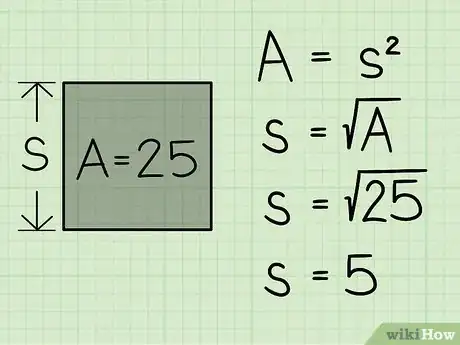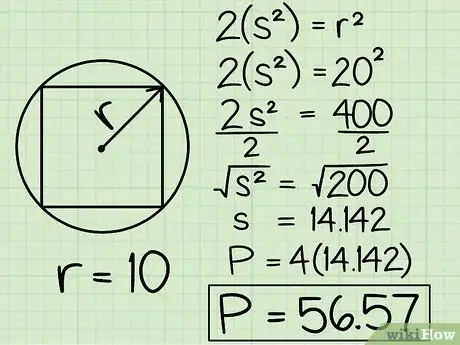Comment calculer le périmètre d’un carré

Le périmètre d'une figure géométrique à deux dimensions est la longueur du bord de cette figure ou la somme des mesures de ses côtés ^{[1]
X
Source de recherche}. Un carré est, par définition, une figure à quatre côtés égaux et dont les quatre angles ont la même mesure (90° ^{[2]
X
Source de recherche}). Comme les quatre côtés sont égaux, il est assez simple de calculer le périmètre d'un carré ! Dans cet article, vous trouverez trois façons de calculer ce périmètre en fonction de certaines données : en ne connaissant que le côté, en n'ayant que la surface ou en partant d'un carré inscrit dans un cercle dont on aurait le rayon.

Méthode 1

Méthode 1 sur 3:
Calculer le périmètre en ne connaissant que le côté

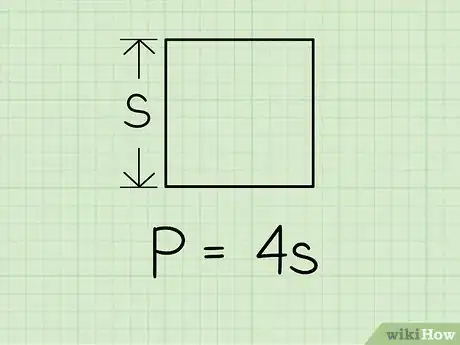
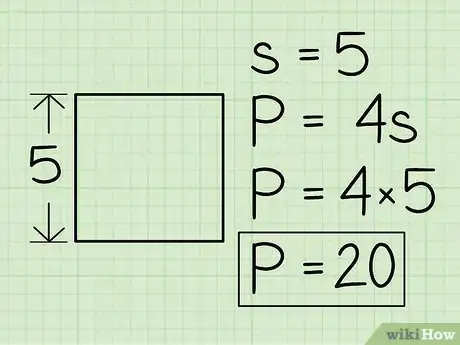
1
Rappelons la formule de calcul du périmètre d'un carré. Si on pose que c est la longueur du côté, alors le périmètre est le quadruple de ce côté : P = 4c.
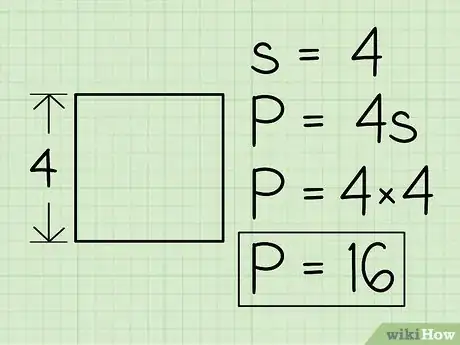
2
Déterminez la longueur d'un des côtés et multipliez-la par 4 pour obtenir le périmètre. Là, deux cas de figure : soit on vous donne directement dans l'exercice la longueur du côté ou de quoi la calculer, soit vous devez la mesurer avec votre règle. Ci-dessous, voyez comment on calcule un périmètre :
- si votre carré a un côté de 4, alors P = 4 x 4, soit 16,
- si votre carré a un côté de 6, alors P = 4 x 6, soit 24.
Publicité

Méthode 2

Méthode 2 sur 3:
Calculer le périmètre en ne connaissant que la surface

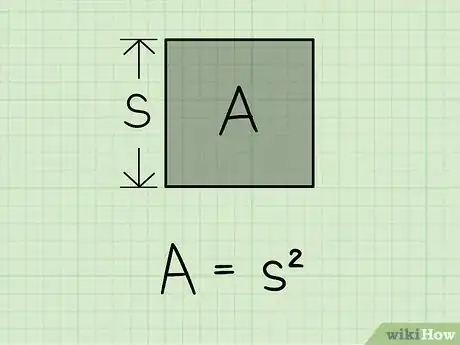
1
Présentons la formule de calcul de l'aire d'un carré. L'aire d'un rectangle (le carré n'est qu'une forme particulière de rectangle) s'obtient en multipliant la longueur par la largeur ^{[3]
X
Source de recherche}. Comme ces deux mesures sont égales dans un carré (longueur = largeur), la surface ou aire (A) d'un carré de côté c est : A = c x c = c².
2
Prenez la racine carrée de la surface. Si vous prenez la racine carrée de la surface, vous allez obtenir la longueur du côté. Le plus souvent, il vous faudra utiliser une calculatrice pour calculer cette valeur. Pour cela, tapez sur votre machine la surface, puis appuyez sur la touche de la racine carrée (√). Une racine carrée peut aussi se calculer à la main.
- Si la surface du carré est de 20, alors le côté c =√20, soit 4,472.
- Si la surface du carré est de 25, alors c = √25, soit 5.
3
Multipliez le côté par 4 pour obtenir le périmètre. Prenez la valeur de c que vous venez d'obtenir et introduisez-la dans la formule du périmètre, P = 4c. Le résultat obtenu est le périmètre de votre carré.
- Pour le carré ayant une surface de 20 et un côté de 4,472, le périmètre est : P = 4 x 4,472, soit 17,888.
- Pour le carré ayant une surface de 25 et un côté de 5, P = 4 x 5, soit 20.
Publicité

Méthode 3

Méthode 3 sur 3:
Calculer le périmètre d'un carré inscrit dans un cercle dont on connait le rayon

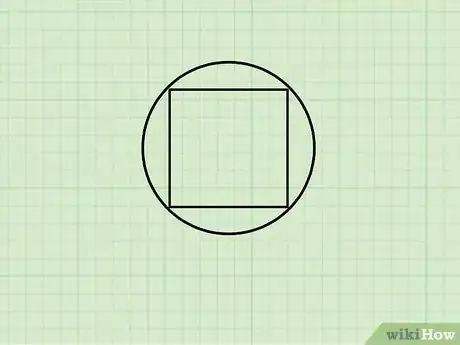
1
Comprenez bien ce qu'est un carré inscrit. On rencontre fréquemment le cercle inscrit dans les examens de type GMAT ou, GRE (évaluations de poursuite d'études), il est donc utile de connaitre ce genre de figure. Un carré inscrit dans un cercle est un carré situé à l'intérieur d'un cercle, en sorte que les quatre angles (coins) du carré se trouvent sur le périmètre ^{[4]
X
Source de recherche}.
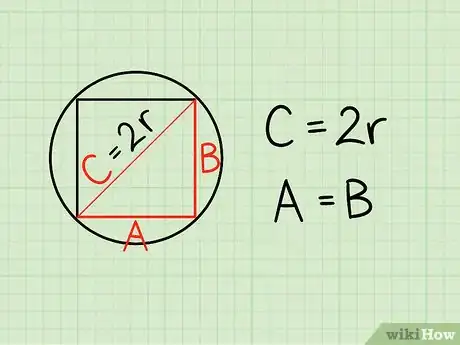
2
Apprenez la relation existant entre le rayon du cercle et la longueur du côté du carré. La longueur qui va du centre du carré inscrit à un des angles est égale au rayon du cercle. Pour trouver le côté du carré, il faut d'abord diviser ce carré en deux triangles rectangles identiques en traçant la diagonale du carré. Chacun de ces triangles a deux côtés égaux, A et B et une hypoténuse C (à ne pas confondre avec le c du côté du carré !), laquelle vaut deux fois le rayon, soit 2r.
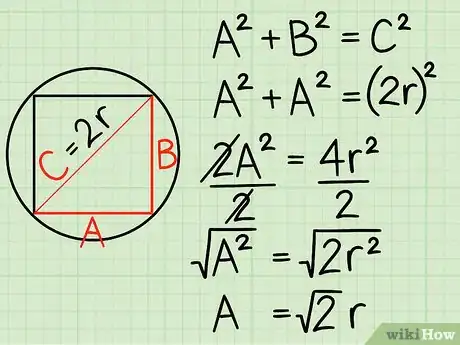
3
Passez par le théorème de Pythagore pour trouver le côté du carré. Ce théorème bien connu stipule que, dans tout triangle rectangle ayant pour côtés A et B et pour hypoténuse C, A² + B² = C² ^{[5]
X
Source de recherche}. Comme ici, A et B sont égaux (c'est un carré !) et que nous savons par ailleurs que C = 2r, on peut récrire l'équation, puis la simplifier afin de trouver le côté du carré :
- A² + A² = (2r)², on simplifie, ce qui donne :
- 2A² = 4r², on divise chaque membre par 2, ce qui donne :
- A² = 2r², on prend la racine carrée de chaque membre, ce qui donne :
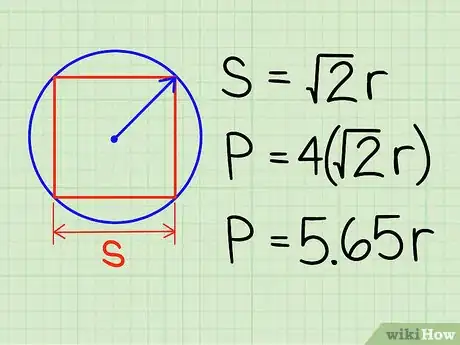
- A = √(2r). Cette longueur A est le côté (c) du carré : A = c = √(2r).
4
Multipliez la longueur du côté par quatre afin d'obtenir le périmètre. Ici, le périmètre du carré est : P = 4√(2r). Grâce à la propriété distributive des racines (qui établit que 4√(2r) est égal à 4√2 x 4√r), on peut en déduire que le périmètre de n'importe quel carré inscrit dans un cercle de rayon r se calcule avec la formule : P = 5,657r ^{[6]
X
Source de recherche}.
5
Résolvez le problème suivant. Prenons un carré (de côté c) inscrit dans un cercle de 10 cm de rayon. En conséquence, la diagonale de ce carré est égale à 2 x 10 cm, soit 20 cm. Selon le théorème de Pythagore, on sait que : 2c² = 20² ou, calcul fait, 2c² = 400. Divisez à présent par 2 de chaque côté : c² = 200. Prenez la racine carrée des deux membres de l'équation : c = √200 = 14,142. Pour terminer, multipliez ce résultat par 4 et vous aurez le périmètre de votre carré : P = 14,142 x 4 = 56,568 cm, arrondi à 56,57 cm.
- Vous auriez pu utiliser la formule, vue précédemment, qui donne le périmètre directement à partir du rayon. Il suffit alors de multiplier le rayon (10 cm) par 5,657 : 10 x 5,657 = 56,57. Le résultat est le même, mais, si vous avez du mal à mémoriser cette formule, passez-en par le théorème de Pythagore.
Publicité