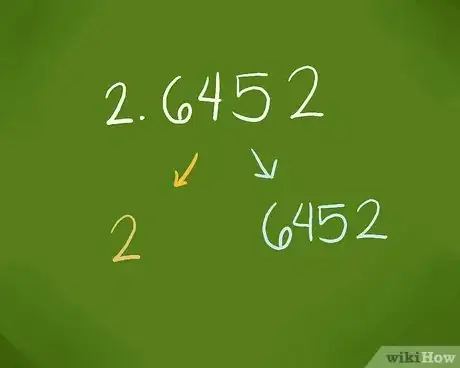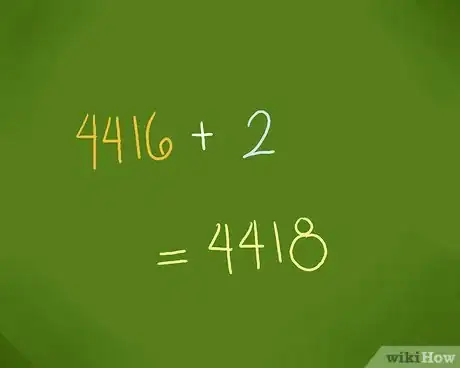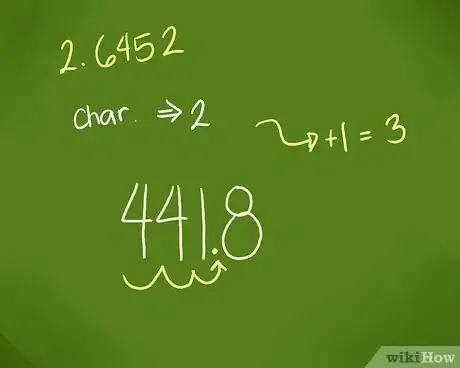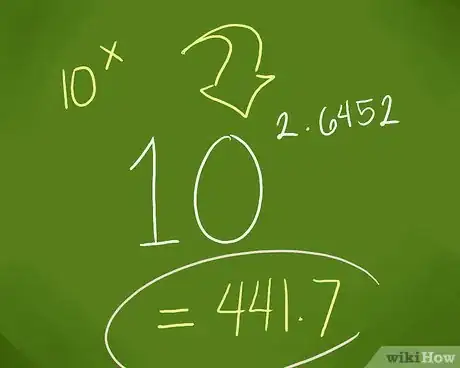Comment calculer un antilog

Informations concernant l'auteur.e

La fonction LOG est une fonction mathématique qui permet de comprimer des données chiffrées. En effet, le logarithme est utilisé quand il s'agit de représenter une série de données ayant une grande amplitude. C'est le cas par exemple en astronomie ou dans les circuits intégrés. On peut donc utiliser le log pour comprimer des données, mais on peut, pour les besoins de la cause, retrouver les données d'origine : on utilise pour cela la fonction inverse du log, aussi appelée réciproque du log ou encore « antilog ». Voyons cela de plus près !

Méthode 1

Méthode 1 sur 2:
Utiliser une table d'antilogs

1
Séparez la partie entière (ou caractéristique) de la mantisse. Voyons cela de plus près. Dans un logarithme (décimal - log(x) - ou népérien - ln(x) -), la partie entière est la série de chiffres qui se situe à gauche de la virgule ; la mantisse est la série de chiffres qui se trouve à droite de la même virgule. Les tables d'antilog se présentent avec dissociation de la partie entière et de la mantisse. C'est la raison pour laquelle il faut commencer par cette étape de séparation.
- Prenons un exemple concret : pour trouver l'antilog de 2,6452, il faut savoir que 2 est la partie entière et 6452 est la mantisse.
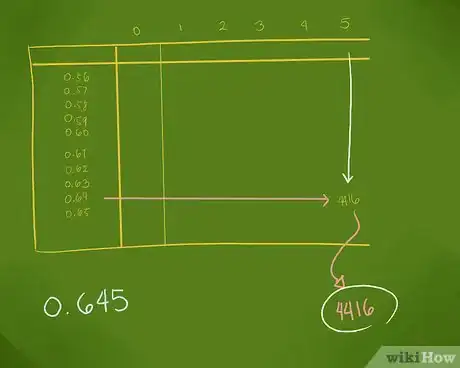
2
Utilisez une table pour trouver la valeur correspondant à la mantisse. Les tables d'antilogs sont faciles à trouver. Si cette notion est à votre programme, vous en trouverez forcément une à la fin de votre manuel de mathématiques. Dans cette table, repérez à gauche la ligne qui correspond aux deux premiers chiffres de votre mantisse. Puis, sur cette même ligne, en vous déplaçant à droite, allez jusqu'à la colonne qui a le même chiffre que votre troisième chiffre de mantisse.
- Dans notre exemple, dans une table, regardez dans la colonne de gauche où se trouve 0,64 (deux premiers chiffres de 0,6452). Puis sur cette ligne, allez à la colonne marquée 5 (troisième chiffre de la mantisse. Vous allez lire 4416.
3
Trouvez la valeur correspondant à la quatrième décimale. Il faut pour cela observer les neuf colonnes qui se trouvent à droite de votre table. On les appelle « colonnes des différences moyennes ». Reprenez la ligne des deux premiers chiffres de la mantisse et, sur cette ligne, récupérez la valeur qui se trouve à l'aplomb de la colonne des différences moyennes et qui correspond au quatrième chiffre de la mantisse.
- Dans notre exemple, on reprend la ligne 0,64, on va tout à droite pour trouver la colonne qui porte le chiffre 2. La valeur trouvée est… 2 !
4
Additionnez les valeurs trouvées précédemment. En effet, après les avoir trouvées, il suffit de les ajouter.
- Dans notre exemple, on a 4416 et 2, ce qui, addition faite, donne 4418.
5
Mettez la virgule. Celle-ci se place à (PE + 1) rangs à partir de la gauche, PE étant la partie entière.
- Dans notre exemple, la partie entière était 2, on ajoute 1, ce qui donne 3. La virgule se place à trois rangs à partir de la gauche. L'antilog de 2,6452 est donc 441,8.
Publicité

Méthode 2

Méthode 2 sur 2:
Calculer l'antilog

1
Observez les deux parties de votre nombre. Pour tout nombre (entier ou décimal), la partie entière est le chiffre ou le nombre qui se situe à gauche de la virgule ; la mantisse est la série de chiffres qui se trouve à droite de la même virgule
- Prenons un exemple concret : pour trouver l'antilog de 2,6452, il faut savoir que 2 est la partie entière et 6452 est la mantisse.
2
Sachez en quelle base est votre logarithme. Tout logarithme se définit sur une base (10, le plus souvent, mais ce peut être 4 ou 20). En calcul numérique, la base est 10. Quand on calcule un antilog, il vaut mieux se souvenir de la base de départ, sinon vous risquez d'avoir quelques problèmes.
3
Calculez 10^x. Par définition, l'antilog d'un nombre x est 10^x. Rappelons que la base est 10 et que x est le nombre dont vous voulez trouver l'antilog. Si la mantisse de votre nombre est 0 (un nombre entier donc !), le calcul est alors facile : multipliez 10 par 10… autant de fois que votre chiffre ou votre nombre de référence (log₁₀(1 000) = 3 - antilog₁₀(3) = 10³ = 10 x 10 x 10 = 1 000). Si votre chiffre ou votre nombre de référence (x) est décimal, ce n'est pas un problème non plus, son antilog est 10^x. Simplement, il faudra une calculatrice pour faire le calcul.
- Dans notre exemple, nous avons un chiffre décimal. Cela ne fait rien. Son antilog est quand même 10^2,6452, ce qui donne, après calcul à la machine, 441,7.
Publicité

Conseils

Les logs et les antilogs sont fréquemment utilisés, tant en calcul numérique que scientifique.
La multiplication et la division des logs sont assez simples. La multiplication se change en addition (log(ab) = log(a) + log(b)) et la division, en soustraction (log(a/b) = log(a) - log(b)).
La partie entière et la mantisse sont les noms des deux parties d'un nombre, situées de part et d'autre de la virgule. Ces termes, ensemble, ne sont pas utilisés en dehors de la fonction log.