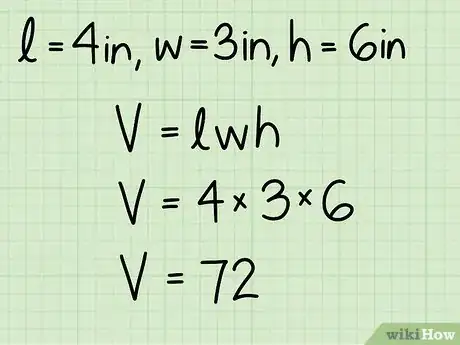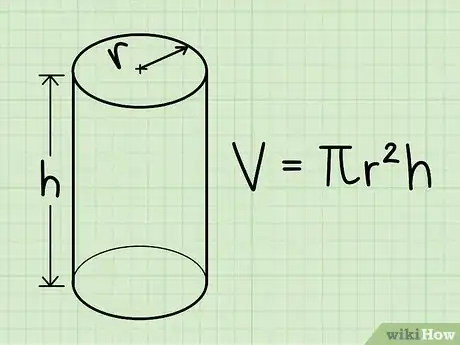X
Cet article a été coécrit par Grace Imson, MA. Grace Imson est une professeure de mathématiques ayant plus de 40 ans d'expérience dans l’enseignement. Grace exerce actuellement au City College de San Francisco. Auparavant, elle était professeure au département de mathématiques de l'université Saint-Louis. Elle a enseigné cette discipline aux niveaux primaire, intermédiaire, secondaire et universitaire. Elle est titulaire d'un master en éducation avec une spécialisation en administration et supervision, délivré par l'université Saint-Louis.
Il y a 11 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 76 133 fois.
Par volume d'un objet tridimensionnel, on entend en fait simplement la quantité d'espace qu'il occupe [1] . Ce peut également être la quantité de matière (air, eau, sable…) qu'il peut contenir. Parmi les nombreuses unités de volume, il y a le centimètre cube (cm3), le mètre cube (m3), le décamètre cube (dam3), et ainsi de suite [2] . Apprenez à calculer le volume de six figures géométriques à trois dimensions, comme des cubes, des sphères ou des cônes. Cela pourra vous être utile dans certains exercices de maths. Vous remarquerez certaines similitudes dans les formules de calcul, ce qui vous aidera à mieux les retenir. Gageons que vous les retiendrez toutes !
Étapes
Méthode 1
Méthode 1 sur 6:Calculer le volume d'un cube
Méthode 1
-
1Sachez reconnaitre un cube. C'est une forme géométrique à trois dimensions qui comporte six faces carrées identiques [3] . Dit autrement, c'est une sorte de boite carrée.
- Un dé à jouer est un exemple classique de cube, mais il y en a d'autres, comme les cubes de lettres pour les enfants ou certains morceaux de sucre.
-
2Notez la formule pour trouver le volume du cube. Les longueurs des côtés étant toutes égales, la formule de calcul du volume du cube est simple : V = a3 avec V, le volume et a, le côté du cube.
- Pour trouver a3, il suffit de multiplier a trois fois par lui-même : a3 = a x a x a.
-
3Trouvez la longueur de n'importe laquelle des arêtes du cube. Dans un exercice, soit on vous donne directement cette longueur, soit vous devez la mesurer à l'aide d'une règle. Les arêtes du cube étant identiques, peu importe laquelle vous mesurez.
- Si vous n'êtes pas sûr d'avoir affaire à un cube, mesurez toutes les arêtes. Si une ou plusieurs arêtes diffèrent, il faudra vous reporter à la partie suivante intitulée « Calculez le volume d'un parallélépipède ».
-
4Dans la formule V = a3, remplacez a par sa valeur et faites les calculs. Admettons que vous ayez un cube de 5 cm, son volume s'obtient ainsi : V = (5 cm)3. Vous faites : 5 cm x 5 cm x 5 cm = 125 cm3, le volume de notre cube !
-
5Donnez votre réponse en unités cubiques ! Dans notre exemple, nous avions un cube avec un côté en centimètres, son volume sera donc donné en centimètres cubes. Autre exemple, un cube de 3 centimètres de côté a un volume de : V = (3 cm)3, soit V = 27 cm3.Publicité
Méthode 2
Méthode 2 sur 6:Calculer le volume d'un parallélépipède
Méthode 2
-
1Sachez reconnaitre un parallélépipède. Un parallélépipède (ou prisme rectangulaire) est une figure à trois dimensions dont les six faces sont des rectangles [4] . Dit autrement, un parallélépipède est un rectangle tridimensionnel, bref une boite !
- Un cube est un parallélépipède particulier dont les six faces sont égales.
-
2Retenez la formule pour calculer le volume d'un parallélépipède. La formule est la suivante : Volume = longueur x largeur x hauteur, soit V = Llh.
-
3Trouvez la longueur du parallélépipède. Supposons que ce dernier soit posé sur une table. Par longueur du parallélépipède, on entend la longueur du côté le plus long reposant sur la table. Cette dimension peut vous être donnée directement si elle est inscrite sur le croquis qui accompagne l'exercice. Si ce n'est pas le cas, vous devrez la mesurer avec une règle ou un ruban mesureur.
- Prenons un parallélépipède qui a une longueur (L) de 4 cm.
- Ne vous focalisez pas trop sur ce problème de longueur, de largeur… En effet, vous devrez de toute façon multiplier les trois différentes dimensions et peu importe l'ordre puisque la multiplication est commutative (abc = bac = cba…).
-
4Trouvez la largeur du parallélépipède. Supposons que ce dernier soit posé sur une table. Par largeur du parallélépipède, on entend la longueur du côté le plus court reposant sur la table. Cette dimension peut vous être donnée directement si elle est inscrite sur le croquis qui accompagne l'exercice. Si ce n'est pas le cas, vous devrez la mesurer avec une règle ou un ruban mesureur.
- Supposez que ce parallélépipède a une largeur (l) de 3 cm.
- Quand on mesure un parallélépipède avec une règle ou un ruban mesureur, on note toutes les mesures avec la même unité. Ne mettez pas une longueur en centimètres et une autre en millimètres. Vos calculs seraient faussés.
-
5Trouvez la hauteur du parallélépipède. Par hauteur, on entend la longueur qui va de la surface sur laquelle repose le parallélépipède jusqu'au sommet dudit parallélépipède. Soit cette valeur vous est donnée directement sur la figure qui accompagne l'exercice, soit vous devez mesurer, avec une règle ou un ruban mesureur, cette longueur sur ce même dessin.
- Admettons que ce parallélépipède ait une hauteur (h) de 6 cm.
-
6Appliquez la formule. Dans la formule de calcul du volume, remplacez les valeurs littérales par les valeurs données dans votre exercice. Faites ensuite les calculs. Pour mémoire : la formule est V = Llh.
- Dans notre exemple, L = 4, l = 3 et h = 6. Finalement, V = 4 x 3 x 6, soit 72.
-
7Donnez votre réponse en unités cubiques ! Notre parallélépipède avait des dimensions en centimètres, son volume doit donc être donné en centimètres cubes, soit 72 centimètres cubes ou 72 cm3.
- Si on avait eu un parallélépipède de 2 cm de long, de 4 cm de large et de 8 cm de hauteur, on obtiendrait un volume de 2 cm x 4 cm x 8 cm, soit 64 cm3.
Publicité
Méthode 3
Méthode 3 sur 6:Calculer le volume d'un cylindre
Méthode 3
-
1Sachez reconnaitre un cylindre. C'est une figure à trois dimensions composée de deux surfaces circulaires opposées et réunies par une surface courbe complète [5] .
- Une bouteille de soda, des piles rondes (AA ou AAA) sont de bons exemples de cylindres.
-
2Retenez la formule de calcul du volume du cylindre. Pour obtenir le volume d'un cylindre, vous devez connaitre sa hauteur et le rayon de sa base circulaire (soit la distance qui va d'un des points de la circonférence au centre du cercle). La formule est donc la suivante : V = πr2h, V étant le volume, r, le rayon de la base circulaire, h, la hauteur et enfin la constante π (« pi »).
- Il peut arriver qu'on vous demande de donner une réponse contenant « pi », mais le plus souvent, on vous demandera faire les calculs jusqu'au bout en prenant pour valeur de « pi », 3,14. En cas de doute, demandez à votre enseignant la forme qu'il désire.
- La formule de calcul du volume d'un cylindre est assez similaire à celle utilisée pour un parallélépipède : il faut multiplier la hauteur de l'objet par l'aire de base (Ab). Avec le parallélépipède, on avait : Ab = L x l ; pour le cylindre, Ab = πr2, r étant le rayon de la base.
-
3Trouvez le rayon de la base. Si le rayon vous est donné sur le croquis, prenez cette valeur. Si c'est le diamètre qui est indiqué, divisez-le par 2 pour avoir le rayon (d = 2r).
-
4Mesurez l'objet si le rayon n'est pas donné d'emblée. Mesurer précisément le rayon d'un objet cylindrique n'est ni facile ni précis. D'habitude, on pose une règle (ruban mesureur) sur le dessus du cylindre, au niveau de sa partie la plus large. Soyez le plus précis possible. Divisez ensuite ce résultat par 2 pour avoir le rayon.
- Il est possible d'obtenir le rayon à partir de la circonférence (pourtour de l'objet). Cette dernière peut être mesurée avec un mètre souple de couturière, par exemple ou avec un morceau de ficelle qu'on enroule autour du cylindre. Avec un crayon, marquez sur la ficelle un tour complet, puis mesurez avec une règle cette distance. Pour avoir le rayon, utilisez la formule suivante : C (circonférence) = 2πr. Divisez la circonférence par 2π (soit 6,28) et vous aurez votre rayon.
- Ainsi, si vous avez trouvé une circonférence de 8 centimètres, c'est que le rayon est de 1,27 cm.
- Si vous désirez une mesure précise, vous pouvez combiner les deux méthodes (mesure du diamètre et celle de la circonférence). Si vos deux résultats divergent, recommencez les mesures jusqu'à avoir deux valeurs identiques. La mesure de la circonférence donne généralement un résultat bien plus fiable et précis.
-
5Calculez l'aire de la base circulaire. Remplacez le r de la formule πr2 par sa valeur réelle. Commencez par multiplier le rayon par lui-même, puis multipliez ce résultat par π. Prenons un exemple :
- si le rayon est de 4 centimètres, l'aire de la base est donc de : A = π42 ;
- A = π42 = π (4 x 4) = 16 x π = 16 x 3,14 = 50,24 cm2 ;
- si on vous donne le diamètre (d) de la base, divisez-le par 2 pour avoir le rayon r (d = 2r).
-
6Trouvez la hauteur du cylindre. Cette dernière est tout simplement la longueur entre les deux bases circulaires (celle du haut et celle du bas) ou encore la longueur entre la surface sur laquelle il est posé et son sommet. Sur un croquis, voyez si on ne vous donnerait pas directement la hauteur. Sinon, mesurez-la avec une règle ou un ruban mesureur.
-
7Multipliez l'aire de la base par la hauteur du cylindre pour obtenir le volume. Vous auriez pu sauter l'étape de calcul de l'aire de base en remplaçant r et h directement dans la formule : V = πr2h. Reprenons notre cylindre de 4 centimètres de rayon et de 10 centimètres de haut :
- V = π4210
- π42 = 50,24
- 50,24 x 10 = 502,4
- V = 502,4
-
8N'oubliez pas de spécifier votre réponse en unités cubiques ! Notre cylindre avait des dimensions en centimètres, son volume doit donc être donné en centimètres cubes : V = 502,4 cm3. Si on avait eu des mètres (pour un silo, par exemple), le volume aurait été en mètres cubes (m3).Publicité
Méthode 4
Méthode 4 sur 6:Calculer le volume d'une pyramide régulière
Méthode 4
-
1Comprenez bien ce qu'on entend par pyramide régulière. C'est une forme géométrique tridimensionnelle ayant un polygone pour base et les faces latérales sont des triangles ayant un sommet commun, appelé « sommet de la pyramide [6] ». Étant donné que, pour une pyramide régulière, le polygone de base est régulier (côtés égaux), toutes les arêtes latérales ont la même longueur et tous les angles sont égaux [7] .
- Le plus souvent, on part d'une pyramide ayant un carré de base. Rien n'empêche d'avoir une base à 5, 6, voire 100 côtés ! Toutes les arêtes convergeront quand même en un seul sommet.
- Une pyramide ayant une base circulaire est appelée « cône » et sera vue plus en détail dans la partie suivante.
-
2Notez la formule pour trouver le volume d'une pyramide régulière. Elle est la suivante : V = 1/3bh, dans laquelle b est l'aire de la base (le fameux polygone du bas) et h, la hauteur, soit la distance qui va du sommet au centre du polygone.
- Cette formule s'applique aussi bien aux pyramides régulières (dont le sommet est sur la même verticale que le centre de la base) qu'aux pyramides irrégulières (dont le sommet est décentré - en oblique - par rapport au centre de la base).
-
3Calculez l'aire de la base. Ici, l'aire de la base sera calculée en fonction de la forme géométrique et du nombre de côtés de ladite base. Les formules seront différentes selon qu'on a un carré, un triangle… Sur notre illustration, on a une pyramide de base carrée dont le côté est de 6 cm. La formule de calcul de l'aire (A) d'un carré est, nous vous le rappelons, la suivante : A = a2 dans laquelle a est le côté. Pour notre pyramide, l'aire de la base est de : (6 cm) 2, soit 36 cm2.
- Si la base est un triangle, la formule de l'aire du triangle est la suivante : A = 1/2bh, avec b représentant la base et h, la hauteur associée.
- Sachez qu'il existe une formule de calcul de l'aire d'un polygone régulier qui s'applique à tous les polygones, quelle que soit la forme : A = 1/2pa, avec A qui représente l'aire, p est le périmètre du polygone et enfin, a, l'apothème, c'est-à-dire la longueur du segment joignant le centre du polygone au milieu d'un côté. Certes, c'est une formule un peu complexe dont l'explication dépasse l'objet de cet article. Pour plus de détails, lisez cet article. Sachez qu'il existe des calculateurs de surface des polygones réguliers en ligne [8] .
-
4Trouvez la hauteur de la pyramide. Dans un exercice, elle vous sera donnée sur le croquis d'accompagnement, comme ici. Dans notre exemple, la hauteur est de 10 centimètres.
-
5Multipliez l'aire de la base de la pyramide par sa hauteur. Puis, divisez par 3 pour trouver le volume. Cette suite d'opérations s'explique par la formule : V = 1/3bh. Dans notre exemple, on avait une pyramide de 30 cm2 de base et de 10 cm de haut, son volume est donc de : 36 x 10 x 1/3 = 120.
- Si la pyramide avait eu une base en forme de pentagone d'une surface de 26 cm2 et de 8 cm de haut, elle aurait eu un volume de : 26 x 8 x 1/3 = 69,33.
-
6N'oubliez pas de spécifier votre réponse en unités cubiques ! Notre pyramide avait des dimensions en centimètres, son volume doit donc être donné en centimètres cubes, à savoir 120 cm3. Si les dimensions avaient été en mètres (pyramide de Chéops, par exemple), le volume aurait été en mètres cubes (m3).Publicité
Méthode 5
Méthode 5 sur 6:Calculer le volume d'un cône
Méthode 5
-
1Faisons connaissance avec les propriétés du cône. C'est une figure à trois dimensions ayant une base circulaire et un sommet. Pour faire simple, c'est une sorte de pyramide, mais avec une base circulaire [9] .
- Si le sommet est aligné verticalement sur le centre de la base, on parle alors de « cône circulaire droit ». Dans tous les autres cas, on a affaire à un « cône quelconque (ou oblique) ». Par chance, la formule de calcul du volume est la même dans les deux cas.
-
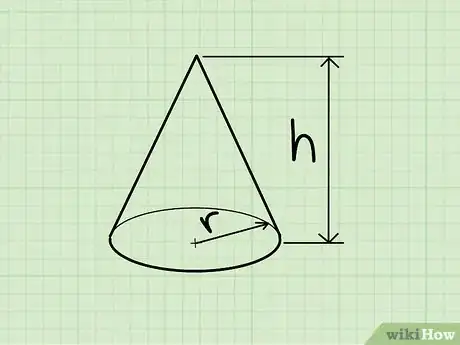
2Retenez la formule qui permet de calculer le volume d'un cône. Elle est la suivante : V = 1/3πr2h, dans laquelle r est le rayon de la base circulaire du cône, h, la hauteur du cône et π, la constante bien connue valant environ 3,14.
- La partie πr2 de la formule correspond en fait à la surface de la base circulaire. Quelque part, la formule du volume du cône est du genre 1/3bh (b = base et h = hauteur)… tout comme la formule du volume de la pyramide vue précédemment !
-
3Calculez l'aire de la base circulaire du cône. Pour ce faire, vous avez besoin de connaitre le rayon de la base, qui doit être donné sur le croquis. Si on vous donnait le diamètre (d), divisez par deux pour avoir le rayon, le diamètre étant égal, par définition à deux fois le rayon (d = 2r). Une fois le rayon (r) connu, servez-vous de cette formule : A = πr2 pour trouver la surface de la base.
- Sur l'illustration, le rayon de la base circulaire du cône est de 3 cm. Quand on remplace r par 3, on obtient : A = π32.
- A = π32 = π (3 x 3) = 9π.
- A = 9π = 9 x 3,14 = 28,27 cm2.
-
4Trouvez la hauteur du cône. Il s'agit de la distance verticale qui sépare la base du cône de son sommet. Dans notre exemple, la hauteur du cône est de 5 centimètres.
-
5Multipliez la hauteur du cône par l'aire de la base. Dans notre exemple, l'aire de la base est de 28,27 cm2 et la hauteur est de 5 cm, donc bh = 28,27 x 5 = 141,35.
-
6Terminez l'opération. Pour finir, multipliez ce résultat par 1/3 (ce qui revient à diviser par 3) et vous aurez le volume du cône. Dans la partie précédente, nous avions un cylindre dont les parois convergeaient vers une surface identique à celle de la base. Avec un cône, ces parois convergent vers un seul point, le sommet : c'est la raison pour laquelle on divise par 3.
- Dans notre exemple, le volume est de : 141,35 x 1/3 = 47,12.
- La formule, adaptée à notre exemple, se présente sous la forme : 1/3π(32)(5) = 47,12.
-
7N'oubliez pas de spécifier votre réponse en unités cubiques ! Le cône ayant été mesuré en centimètres, son volume le sera en centimètres cubes : 47,12 cm3.Publicité
Méthode 6
Méthode 6 sur 6:Calculer le volume d'une sphère
Méthode 6
-
1Voyons ce qu'est une sphère. Une sphère est un objet circulaire à trois dimensions dont tout point de la surface est à égale distance du centre. Dit de façon simpliste, une sphère a une forme de boule, de balle [10] .
-
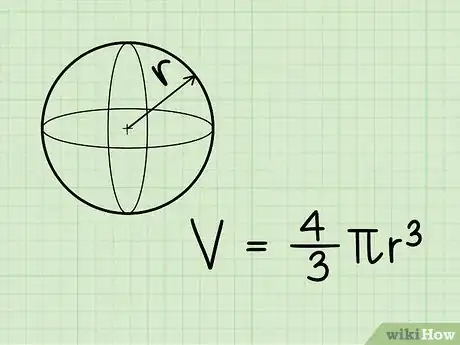
2Notez la formule pour trouver le volume d'une sphère. Elle est la suivante : V = 4/3πr3 (ou si vous préférez, « quatre tiers de pi-r cube »), r étant le rayon de la sphère et π, la fameuse constante dont la valeur est égale à 3,14 [11] .
-
3Trouvez le rayon de la sphère. Si le rayon est donné sur un croquis, il faut juste le retrouver. Si on vous donne le diamètre, divisez par deux pour avoir le rayon. Admettons qu'on ait comme ici une sphère de 3 cm de rayon.
-
4Mesurez la circonférence de la sphère si on ne vous donne pas le rayon. Pour mesurer le pourtour d'un objet sphérique (une balle de tennis, par exemple), il vous faut un bout de ficelle que vous enroulerez autour de la balle au niveau de sa partie la plus renflée. Faites une marque sur la ficelle quand vous aurez fait un tour complet. Il ne reste alors plus qu'à mesurer cette longueur (circonférence) avec une règle. Divisez cette valeur par 2π (= 6,28) et vous aurez le rayon de votre sphère.
- Ainsi, vous avez une balle qui fait 18 cm de circonférence. Divisez cette valeur par 6,28 et vous aurez votre rayon, soit 2,87 cm.
- Mesurer la circonférence d'un objet sphérique n'est pas chose précise. Aussi faut-il prendre trois mesures de circonférence et ne retenir que la moyenne (vous additionnez les trois mesures et vous divisez par trois). Votre résultat sera alors très proche de la vraie mesure.
- Ainsi, admettons que vous ayez effectué trois mesures de circonférence : 18 cm, 17,75 cm et 18,2 cm. Vous additionnez les trois (18 + 17,5 + 18,2 = 53,95) et vous divisez par 3 (53,95 / 3 = 17,98 cm). C'est cette valeur que vous utiliserez pour vos calculs.
-
5Élevez le rayon au cube (r3). Élever un nombre au cube consiste simplement à le multiplier trois fois par lui-même. Ici, r3 = r x r x r. Dans notre exemple, comme r = 3, on a r3 = 3 x 3 x 3 = 27.
-
6Multipliez alors ce résultat par 4/3. Soit vous prenez une calculatrice, soit vous effectuez le produit à la main en simplifiant la fraction finale. Dans notre exemple, on multipliera 27 par 4/3, soit 108/3, c'est-à-dire 36.
-
7Multipliez enfin alors ce résultat par π pour avoir le volume de la sphère. Dernière étape : la multiplication de ce résultat par la constante π. Dans un exercice scolaire, une valeur de π à deux décimales est largement suffisante, à moins que votre enseignant ne vous donne une autre valeur plus précise. Multipliez par 3,14 et vous aurez fini.
- Dans notre exemple, 36 x 3,14 = 113,09.
-
8Donnez votre réponse en unités cubiques ! Dans notre exemple, le rayon de la sphère était en centimètres, la réponse est : V = 113,09 centimètres cubes (113,09 cm3).Publicité
Références
- ↑ http://www.mathsisfun.com/definitions/volume.html
- ↑ http://www.mathsisfun.com/measure/us-standard-volume.html
- ↑ https://www.mathsisfun.com/definitions/cube.html
- ↑ http://www.algebralab.org/lessons/lesson.aspx?file=Geometry_3Dprisms.xml
- ↑ https://www.mathsisfun.com/definitions/cylinder.html
- ↑ http://www.mathwords.com/p/pyramid.htm
- ↑ http://www.mathwords.com/r/regular_pyramid.htm
- ↑ http://www.calculatorsoup.com/calculators/geometry-plane/polygon.php
- ↑ http://www.mathopenref.com/cone.html
À propos de ce wikiHow
Grace Imson, MA
Professeure de mathématiques au City College of San Francisco
Cet article a été coécrit par Grace Imson, MA. Grace Imson est une professeure de mathématiques ayant plus de 40 ans d'expérience dans l’enseignement. Grace exerce actuellement au City College de San Francisco. Auparavant, elle était professeure au département de mathématiques de l'université Saint-Louis. Elle a enseigné cette discipline aux niveaux primaire, intermédiaire, secondaire et universitaire. Elle est titulaire d'un master en éducation avec une spécialisation en administration et supervision, délivré par l'université Saint-Louis. Cet article a été consulté 76 133 fois.
Catégories: Calculs
Résumé de l'articleX
Pour calculer le volume V d'un cube, servez-vous de la formule : V = a au cube, a étant la longueur d'un des côtés du cube. Pour calculer le volume V d'un cylindre, servez-vous de la formule : V = h multiplié par π multiplié par r au carré, r étant le rayon de la base, h la hauteur du cylindre et pi la constante bien connue. Pour calculer le volume V d'un parallélépipède, servez-vous de la formule : V = la longueur multipliée par la largeur multiplié par la hauteur.
Publicité
