Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 57 573 fois.
Tout le monde sait à peu près ce qu'est la vitesse d'un objet : c'est la mesure d'une distance parcourue en un temps donné. L'accélération et la décélération sont aussi à peu près connues dans la mesure où c'est la variation de la vitesse, respectivement à la hausse ou à la baisse, d'un objet. On parlait ici d'une vitesse linéaire, en ligne droite. Lorsque l'objet en mouvement décrit un cercle, comme une roue de voiture ou un cédérom en action, la vitesse et l'accélération sont généralement mesurées par rapport à l'angle de rotation : on parle alors respectivement de vitesse angulaire et d'accélération angulaire. Si vous connaissez la vitesse d'un objet en rotation sur une période donnée, vous allez pouvoir calculer son accélération angulaire moyenne. Il est aussi possible, moyennant une formule particulière, de calculer l'accélération angulaire instantanée, c'est-à-dire à un instant précis.
Étapes
Méthode 1
Méthode 1 sur 3:Calculer une accélération angulaire instantanée
-
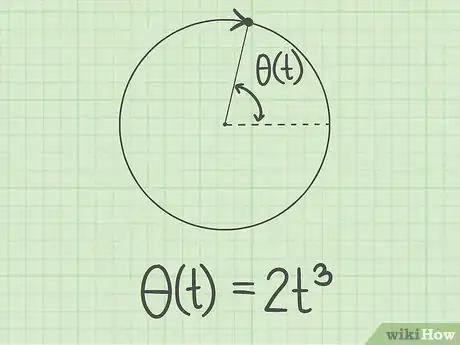
1Calculez la position angulaire d'un objet en rotation. Il existe pour chaque objet en rotation une fonction qui donne la position de l’objet en fonction du temps écoulé. Cette fonction peut vous être donnée, si c’est un exercice scolaire, mais vous pouvez l’établir en ayant fait plusieurs expériences. Il s’agit en fait d’une fonction dérivée. Ici, nous travaillerons à partir d’une fonction qui a été préalablement établie [1] .
- Prenons un exemple théorique. Admettons que, pour un objet donné en rotation homogène, on ait la fonction suivante : , dans laquelle est la position angulaire de l'objet en rotation après un parcours de t secondes et , le temps écoulé depuis le départ de l'objet.
-
2Calculez la vitesse angulaire d'un objet en rotation. La vitesse est la mesure d'une distance parcourue en un temps donné. De façon plus technique et plus large, la vitesse mesure le rapport d'une évolution au temps. Pour un objet en rotation, sa vitesse se calcule en dérivant la fonction de la position par rapport au temps. Le symbole de la vitesse angulaire est . La vitesse angulaire est le plus souvent exprimée en radians par unité de temps (radians par minute, radians par seconde) [2] .
- Dans notre exemple, il faut trouver la dérivée première par rapport au temps de la fonction , soit :
- En fonction de l'exercice donné ou de l'expérience faite, cette dérivée peut servir de deux façons : soit elle vous permettra de connaitre la position d'un objet à un instant , soit elle sera une étape intermédiaire pour le calcul de l'accélération angulaire.
- Dans notre exemple, il faut trouver la dérivée première par rapport au temps de la fonction , soit :
-
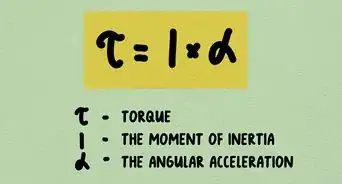
3Calculez l'accélération angulaire d'un objet en rotation. En physique, l’accélération permet de mesurer la variation de la vitesse d’un objet au cours du temps. Mathématiquement, pour obtenir l'accélération angulaire, il faut dériver la fonction de la vitesse angulaire. L'accélération angulaire est conventionnellement indiquée par la lettre grecque (« alpha »). L'accélération angulaire s'exprime par une vitesse par unité de temps, en général des radians par unité de temps au carré (radians par seconde carrée, radians par minute carrée, etc.) [3] .
- Précédemment, nous nous sommes servis de la dérivée de la fonction de la position pour trouver la vitesse angulaire . Pour trouver l'accélération, il faut dériver par rapport au temps, la dérivée seconde en quelque sorte de la fonction de la position, ce qui donne :
- Précédemment, nous nous sommes servis de la dérivée de la fonction de la position pour trouver la vitesse angulaire . Pour trouver l'accélération, il faut dériver par rapport au temps, la dérivée seconde en quelque sorte de la fonction de la position, ce qui donne :
-
4Faites l’application numérique avec les données d’un objet en rotation. Après avoir dérivé la fonction de la vitesse qui était déjà la dérivée de la fonction de la position, vous avez obtenu la fonction de l’accélération instantanée d’un certain objet en rotation. Il ne vous reste plus qu’à l’utiliser pour connaitre l’accélération angulaire instantanée de l'objet à n’importe quel instant t [4] .
- Reprenons l'exemple que nous avons depuis le départ. Nous avons un objet, dont la position angulaire à l'instant t () est donnée par l'équation : , et on vous demande de calculer l'accélération angulaire de l'objet au bout de 6,5 secondes. Servez-vous pour cela de l'équation de trouvée précédemment, remplacez les variables par vos valeurs, puis faites les calculs :
- Votre réponse se doit d'être donnée en radians par seconde carrée. Ainsi, au bout de 6,5 secondes, l'accélération angulaire de l'objet en rotation est de 78 radians par seconde carrée (78 rad/s2).
Publicité - Reprenons l'exemple que nous avons depuis le départ. Nous avons un objet, dont la position angulaire à l'instant t () est donnée par l'équation : , et on vous demande de calculer l'accélération angulaire de l'objet au bout de 6,5 secondes. Servez-vous pour cela de l'équation de trouvée précédemment, remplacez les variables par vos valeurs, puis faites les calculs :
Méthode 2
Méthode 2 sur 3:Calculer une accélération angulaire moyenne
-
1Récupérez la vitesse angulaire initiale. La première méthode pour calculer une accélération angulaire () consiste à diviser la variation de la vitesse angulaire () sur une période donnée par la variation de temps correspondante, la formule est finalement assez simple [5] .
- Prenons l'exemple d'un cédérom qu'on placerait dans un lecteur : il est à l'arrêt, sa vitesse initiale est donc nulle (0 m/s).
- Prenons également l’exemple des roues d’un charriot d’un manège de montagnes russes. Supposons que ces roues tournent à une vitesse de 400 tours à la seconde, soit 2 513 radians à la seconde. En cas de freinage (accélération négative), cette vitesse de rotation sera la vitesse angulaire initiale.
-
2Récupérez la vitesse angulaire finale. Pour pouvoir calculer l’accélération, vous avez aussi besoin d’une deuxième donnée : la vitesse angulaire de l’objet en rotation à la fin de l’expérience. En deux mots, c’est la vitesse finale [6] .
- Généralement, en mode lecture, un cédérom tourne à une vitesse angulaire de 160 radians par seconde.
- Les roues d'un charriot des montagnes russes auront, par définition, une vitesse angulaire nulle en fin de freinage. Cette donnée sera la vitesse angulaire finale.
-
3Mesurez le temps écoulé. Pour pouvoir calculer une vitesse angulaire angulaire d'un objet en rotation homogène, vous devez impérativement connaitre la durée de rotation. Cette donnée peut être donnée si vous travaillez dans le cadre d'un problème scolaire, sinon vous pouvez la mesurer vous-même lors de l'expérience [7] .
- Dans la notice fournie avec le lecteur de cédérom, vous verrez que le disque atteint sa vitesse de lecture en 4 secondes.
- Dans le cas des montagnes russes, on posera que le constructeur garantit, tests à l'appui, l'arrêt complet du train, dès lors qu'on freine, au bout de 2,2 secondes.
-
4Calculez l'accélération angulaire moyenne. Pour pouvoir utiliser la formule, il vous faut donc la vitesse angulaire initiale, la vitesse angulaire finale et le temps écoulé. Ces données seront introduites dans l’équation et, calculs faits, vous obtiendrez l’accélération angulaire moyenne [8] .
- Dans le cas du cédérom qui tourne, le calcul est le suivant :
- rad/s2
- Dans l’exemple des montagnes russes, le calcul est le suivant :
- rad/s2
- Retenez qu'une accélération s’exprime toujours avec une unité qui est une distance par unité de temps au carré. Avec une accélération angulaire, la distance est le plus souvent en radians, mais elle peut être exprimée en tours ou en unité métrique.
Publicité - Dans le cas du cédérom qui tourne, le calcul est le suivant :
Méthode 3
Méthode 3 sur 3:Bien comprendre une accélération angulaire
-
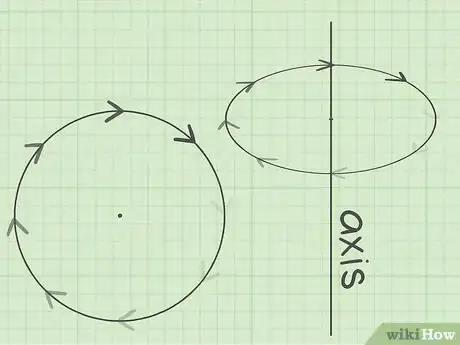
1Comprenez bien ce qu'est un déplacement angulaire. Généralement, quand on parle de vitesse, on pense quasi systématiquement à une vitesse linéaire, un objet qui se déplace en ligne droite, à l'image d'une voiture sur une ligne droite, d'un avion qui décolle ou d'une balle qui est lancée au loin. Cependant, nombre d’objets ont un déplacement angulaire soit en rotation soit en révolution. Pensez, par exemple, à la Terre tournant sur elle-même autour de son axe (rotation). Pour tous ces objets en rotation, on exprime la position et la vitesse avec des unités d’angle. Un déplacement angulaire peut être mesuré pour un cédérom qui est en fonction (un disque vinyle, si vous êtes nostalgique), des électrons qui tournent sur leurs orbites, une roue de voiture qui tourne autour de son axe [9] .
-
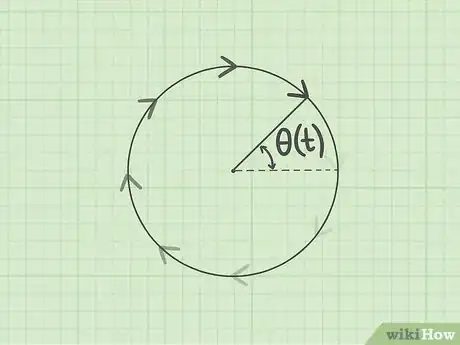
2Visualisez la position angulaire. Avec un objet ou un véhicule se déplaçant en ligne droite, il est assez facile de mesurer la distance parcourue depuis un point A jusqu'à un point B. Si l'objet est cette fois en rotation, on ne mesure plus le déplacement par une distance, mais par un angle de la trajectoire circulaire. Par convention, le point de départ se situe à l'intersection du cercle et du rayon horizontal droit. La distance parcourue est mesurée par l'angle () formé entre ce rayon et la position d'arrêt ou d'observation de l'objet [10] .
- L'angle qui sera mesuré est traditionnellement marqué par la lettre grecque (« thêta »).
- Un déplacement angulaire est dit « positif » quand il s'effectue dans le sens des aiguilles d'une montre, « négatif » quand il s'effectue en sens inverse.
-
3Mesurez le déplacement angulaire en radians. Les déplacements linéaires sont exprimés en une unité de longueur, comme le centimètre, le mètre ou le kilomètre. Les déplacements angulaires le sont le plus souvent en une unité appelée « radian ». Un radian représente une certaine fraction d'un cercle. Un angle d'un radian correspond à un arc de cercle d'une longueur égale au rayon du cercle [11] .
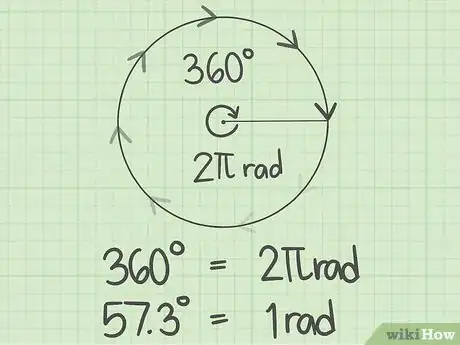
- Un cercle entier représente un angle de 2π radians, si bien qu'un demi-cercle ne représente plus que π radians et un quart de cercle, π/2 radian.
- Il est parfois nécessaire de convertir les radians en degrés. Comme un cercle représente 360 degrés ou 2π radians, vous pouvez établir les correspondances suivantes :
-
- En conséquence, un radian vaut environ 57,3 degrés.
-
4Comprenez bien ce qu'est l'accélération angulaire. L'accélération angulaire est la variation de la vitesse angulaire d'un objet en rotation au cours du temps, cette variation étant plus ou moins rapide, ou lente. Autrement dit, la rotation ou la révolution d’un objet peut ralentir ou s’accroitre. Si vous connaissez la vitesse angulaire à un moment donné et cette même vitesse un instant plus tard, vous pouvez calculer l’accélération angulaire moyenne sur l'espace de temps concerné. On l’a vu, à partir de la fonction de la position d’un objet en rotation, vous pouvez en déduire la fonction de l’accélération instantanée angulaire par rapport au temps [12] .
- Dans le langage courant, les gens parlent d'accélération pour dire qu'un objet va plus vite et de décélération pour dire que ce même objet va moins vite. En mathématiques et en physique, seule existe la notion d'accélération. Si l'objet accélère, on parle d'accélération positive, s'il ralentit, on parle d'accélération négative.
Publicité
Conseils
- Ne mélangez pas les unités ! La position angulaire s'exprime le plus souvent en radians (rad), la vitesse angulaire, en radians par unité de temps (rad/s), tandis que l'accélération angulaire s'exprime en radians par unité de temps au carré (rad/s2).
Références
- ↑ http://physics.tutorvista.com/motion/angular-acceleration.html
- ↑ http://physics.tutorvista.com/motion/angular-acceleration.html
- ↑ http://physics.tutorvista.com/motion/angular-acceleration.html
- ↑ http://physics.tutorvista.com/motion/angular-acceleration.html
- ↑ http://www.softschools.com/formulas/physics/angular_acceleration_formula/153/
- ↑ http://www.softschools.com/formulas/physics/angular_acceleration_formula/153/
- ↑ http://www.softschools.com/formulas/physics/angular_acceleration_formula/153/
- ↑ http://www.softschools.com/formulas/physics/angular_acceleration_formula/153/
- ↑ http://physics.tutorvista.com/motion/angular-acceleration.html



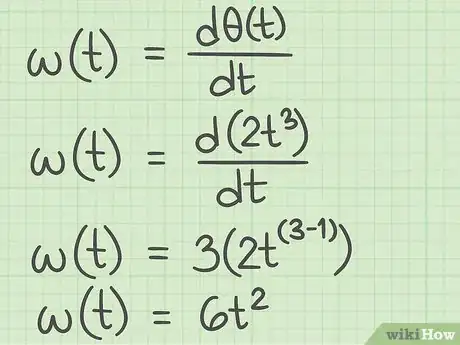


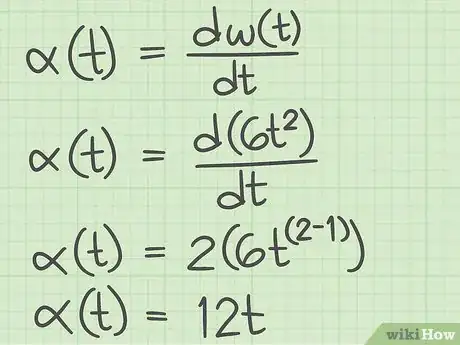



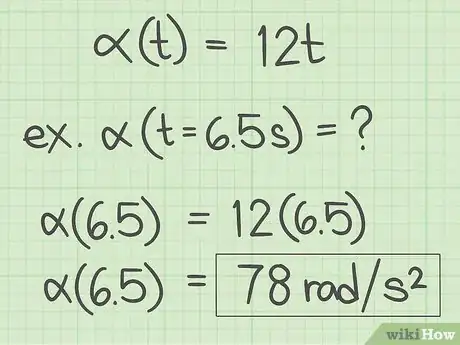

















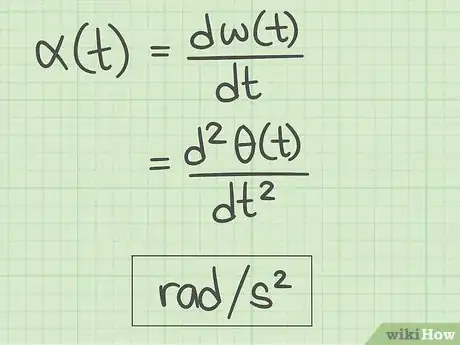












L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 57 573 fois.