Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 20 565 fois.
Avec les calculatrices d’aujourd’hui, extraire une racine cubique est une simple affaire de touches à manipuler. Si vous n’avez pas de calculatrice ou si vous voulez épater des amis, sachez qu’il est possible d’extraire une racine cubique avec un crayon et du papier. La technique est peut-être un peu laborieuse au départ, mais avec de l’entrainement, elle est certes longue, mais facile. Avec quelques notions d’arithmétique et d’algèbre, vous saurez facilement extraire une racine cubique.
Étapes
Partie 1
Partie 1 sur 3:Extraire une racine cubique à l’aide d’un exemple
-
1Posez bien le problème. Extraire une racine cubique, c’est se livrer à quelque chose qui s’apparente à une série de divisions… à quelques différences près. La première étape consiste à présenter correctement le nombre dont vous voulez extraire la racine cubique [1] .
- Inscrivez le nombre dont vous souhaitez la racine cubique. Notez-le sous une forme spéciale, à savoir par groupe de trois chiffres, en utilisant éventuellement une virgule. Admettons que vous vouliez la racine cubique de 10. Inscrivez 10 sous la forme suivante : 10, 000 000. Ces zéros qu’on rajoute vont permettre de calculer une racine précise.
- Mettez ce nombre sous le symbole de la racine cubique. Le trait horizontal jouera un peu le rôle d’une barre de division, mais c’est un simple trait de séparation.
- Placez d’entrée de jeu une virgule au-dessus de la barre de la racine et à l’aplomb de la virgule de votre nombre.
-
2Apprenez par cœur les dix premiers cubes. Cela vous sera utile par la suite. Ils sont les suivants :
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
-
3Trouvez le premier chiffre de la racine. Sélectionnez un chiffre qui, élevé au cube, donne une valeur approchante du nombre de la série, sans cependant le dépasser [2] .
- Précédemment, nous avons dressé la liste des dix premiers cubes. Trouvez le chiffre qui donne le cube le plus élevé, mais inférieur à votre nombre de départ (10). Ici, c’est 8 qui est le cube de 2.
- Inscrivez ce chiffre 2 au-dessus de la barre horizontale de la racine et à l’aplomb de votre 10. Sous le 10, placez le cube de ce 2, soit 23, soit 8. Tracez en dessous un trait horizontal et faites la soustraction entre 10 et 8, ce qui vous donne 2.
- Cette opération faite, vous avez tout en haut le premier chiffre significatif de votre racine. Il est très rare que cette réponse suffise, c’est pourquoi il faut des décimales. En effet, si votre réponse était 2, vous seriez assez loin de la vraie réponse, puisque et non pas 10 : il faut aller plus loin.
-
4Cherchez la première décimale. À côté du reste obtenu, abaissez le groupe de trois chiffres qui suit dans le nombre de départ. Tracez un petit trait vertical à gauche de ce nouveau nombre. C’est ce dernier chiffre qui va servir à trouver la première décimale de la racine cubique. Dans notre exemple, il restait 2, on abaisse le groupe 000, ce qui donne 2 000 [3] .
- À gauche du petit trait vertical, vous allez préparer une somme de trois valeurs en laissant trois espaces blancs un peu larges, séparés par un signe « + ». La somme sera le futur diviseur.
-
5Trouvez la première composante du diviseur. Elle a été laissée en blanc et pour la trouver, inscrivez le total du produit de 300 par le carré du chiffre qui est au-dessus de la barre horizontale de la racine. Dans notre exemple, le chiffre du haut (soit 2) est d’abord élevé au carré, ce qui donne 4 (22 = 4), puis multiplié par 300, ce qui donne 1 200. Dès lors, cette valeur de 1 200 sera inscrite sur le premier blanc. Vous n’avez pas encore le diviseur, mais seulement une partie de sa valeur à savoir 1 200, à laquelle il faut ajouter quelque chose [4] .
-
6Trouvez le deuxième chiffre de votre racine cubique. Vous aviez un reste de 2 000 et vous avez trouvé un diviseur, 1 200 et quelque chose : vous devez trouver combien de fois il va 1 200 et des poussières dans 2 000. Il n’y a qu’une seule réponse et c’est 1. 2 ne peut pas aller, car 2 x (1 200 + x) donnera plus de 2 400, bien supérieur donc à 2 000. Inscrivez ce chiffre (1) au-dessus de la barre horizontale de la racine et à la droite du 2 déjà présent [5] .
-
7Déterminez le reste du diviseur. Nous avons dit que le diviseur se compose de trois éléments. Le premier a déjà été trouvé, puisqu’il s’agit du 1 200 de l’étape précédente. Il faut trouver les deux autres éléments [6] .
- Multipliez 3 par 10, puis par les deux chiffres, séparément, qui se trouvent au-dessus de la barre horizontale de la racine. Dans notre exemple, il faut faire : 3 × 10 × 2 × 1, soit 60. Ajoutez ce résultat à celui déjà trouvé, soit 1 200 et vous obtenez 1 260.
- Enfin, il faut ajouter à ce résultat le carré du dernier chiffre, celui situé au-dessus de la barre horizontale de la racine. Dans notre exemple, c’est 1 qui, élevé au carré, donne toujours 1. On additionne tous les éléments : 1 200 + 60 + 1, soit 1261, le diviseur est 1261. Notez-le à gauche du trait vertical.
-
8Multipliez, puis soustrayez. L’étape présente consiste à prendre à nouveau ce dernier chiffre, c’est donc à nouveau 1 et à le multiplier par le diviseur que vous venez juste de calculer, ce qui donne : 1 × 1261 = 1 261. Inscrivez ce résultat sous 2 000, puis faites la soustraction, ce qui donne 739.
-
9Voyez si vous avez besoin d’une réponse plus précise. Vous avez déjà fait deux soustractions et vous avez une racine cubique avec deux chiffres significatifs. Si vous en voulez d’autres, vous devrez continuer cette façon de faire. Nous cherchions au départ la racine cubique de 10. Après la première soustraction, vous n’aviez comme réponse que 2, ce qui était bien imprécis. Après une deuxième série de calculs, vous avez une racine cubique de 2,1, ce qui est un peu plus précis [7] .
- Vous pouvez apprécier le degré de précision en élevant 2,1 au cube : 2,1 × 2,1 × 2,1, soit 9,261.
- Si c’est là la précision que vous vouliez, l’exercice est fini. Si vous estimez que la précision n’est pas suffisante, vous devez procéder à une autre série de calculs.
-
10Trouvez le prochain diviseur. Si vous désirez affiner votre résultat, faites la même série de calculs que précédemment, les nombres étant évidemment différents [8] .
- Abaissez le prochain groupe de trois chiffres. Dans notre exemple, il faut abaisser 000 qu’on met à côté du reste 739, ce qui nous donne 739 000.
- Calculez la première partie du diviseur en faisant 300 fois le carré du nombre situé au-dessus de la barre horizontale de la racine. Dans notre exemple, cela donne : , soit 132 300.
- Pour trouver le troisième chiffre significatif de votre racine, vous devez trouver combien de fois il va 132 300 dans 739 000. Pour notre exemple, il faut prendre 5, car 5 × 132 300 = 661 500. Inscrivez 5 à droite du chiffre déjà présent au-dessus de la barre horizontale de la racine.
- Multipliez 3 par 10, puis par le nombre composé des deux premiers chiffres qui se trouve au-dessus de la barre horizontale de la racine, puis par le dernier chiffre de la racine, ce qui donne : .
- Pour finir, élevez au carré ce dernier chiffre, ce qui donne :
- Ajoutez tous les éléments du diviseur et vous obtiendrez : 132 300 + 3 150 + 25 = 135 475.
-
11Multipliez ce diviseur par le dernier chiffre significatif. Vous avez calculé votre nouveau diviseur et vous avez un nouveau chiffre significatif pour votre racine, il faut à présent les multiplier entre eux.
- Multipliez le diviseur par le dernier chiffre significatif : 135 475 × 5 = 677 375.
- Comme précédemment, faites la soustraction : 739 000 - 677 375 = 61 625.
- C’est à vous de voir si 2,15 est une racine assez précise. Pour cela, élevez cette valeur au cube : .
-
12Inscrivez votre résultat. Le nombre qui se trouve au-dessus de la barre horizontale de la racine est votre résultat. Ici, d’après vos calculs, vous avez trouvé que la racine cubique de 10, avec trois chiffres significatifs, était 2,15. Vous avez aussi vérifié que 2,153 = 9,94, qui n’est certes pas tout à fait 10. Si vous désirez un résultat plus précis, il ne vous reste plus qu’à recommencer une nouvelle série de calculs. Vous pouvez en faire autant que voulez.Publicité
Partie 2
Partie 2 sur 3:Trouver une racine cubique par encadrements successifs
-
1Encadrez votre valeur entre deux cubes parfaits. Encadrer un nombre signifie trouver deux valeurs entières successives qui, élevées au cube, donneront respectivement la valeur juste inférieure à la racine recherchée et celle juste supérieure.
- Admettons que vous deviez chercher la racine cubique de 600. Vous pouvez encadrer ce nombre entre deux racines cubiques, à savoir et . Ce faisant, vous savez désormais que la racine cubique de 600 se situe entre 8 et 9. Les valeurs 512 et 729 sont ainsi la limite basse et haute de votre encadrement.
-
2Estimez la première décimale. Vous avez encadré votre racine cubique entre deux valeurs, mais ce n’est pas assez précis. Vous devez resserrer votre encadrement en supposant une première décimale entre 0 et 9, laquelle devra être logique.
- En reprenant notre exemple concret, vous voyez que 600 est à peu près à mi-chemin de 512 et 729 : vous pouvez donc tester 5 comme première décimale.
-
3Élevez cette estimation au cube. En faisant cette opération, vous allez voir si vous vous êtes rapprochés de votre valeur de départ et dans quel sens.
- Reprenons notre exemple. Faites le calcul suivant : .
-
4Refaites une estimation. Vous venez d’élever au cube votre estimation, il faut l’ajuster. Si vous avez dépassé votre nombre de départ, prenez une décimale inférieure d’une ou deux unités. Si votre cube est inférieur au nombre de départ, il faut alors augmenter votre décimale d’une ou deux unités.
- Reprenons notre exemple. On voit que est supérieur à 600. Il faut donc essayer 8,4. Élevez-le au cube et voyez ce que cela donne. Faites le calcul suivant : . Cette fois, vous êtes en dessous de votre valeur, si bien que vous pouvez en conclure que la racine de 600 se situe, sans plus de précision, entre 8,4 et 8,5.
-
5Estimez la deuxième décimale. Pour obtenir une racine plus précise, vous devez procéder de la même façon, mais avec deux décimales cette fois. Choisissez une décimale logique entre 0 et 9, puis testez-la en élevant votre approximation. Comme précédemment, ajustez la décimale en fonction du résultat obtenu.
- En reprenant notre exemple concret, vous avez trouvé que et que . Vous voyez que 600 est à mi-distance des deux valeurs, mais plus proche de 592,7 que de 614,1. Il serait bien d’essayer de choisir comme deuxième décimale 4, ce qui revient à élever au cube 8,44.
-
6Encadrez de façon plus resserrée. Utilisez la même méthode pour affiner votre résultat. Trouvez les deux valeurs, avec une décimale de plus chaque fois, qui, élevées au cube, encadrent votre valeur de départ.
- Reprenons notre exemple et essayons avec 8,44. On fait : . Nous sommes donc juste au-dessus de notre nombre (600), ce qui fait que nous essayons 8,43. L’élévation au cube donne : . En conséquence, la racine cubique de 600 est comprise entre 8,43 et 8,44.
-
7Continuez autant de fois que désiré. Cette procédure d’encadrement peut être répétée à l’envi, tout va dépendre en fait du nombre de décimales et donc de la précision, que vous voulez. Plus vous aurez de décimales, plus les cubes seront proches de votre valeur de départ.
- Pour la racine cubique de 600, on avait trouvé que 8,43 était très proche de la solution. Nous allons donc tenter une troisième décimale avec 8,434, ce qui donne : . On est plus très loin de la bonne réponse !
Publicité
Partie 3
Partie 3 sur 3:Comprendre le principe de ce mode de calcul de la racine cubique
-
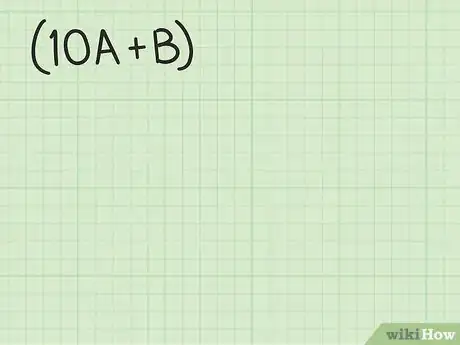
1Révisez le principe du développement des binômes au cube. Pour comprendre ce qui va suivre, vous allez devoir piocher dans votre mémoire, si vous avez fait des études secondaires, pour vous rappeler comment on élève au cube un binôme. Comme tout le monde n’a pas forcément suivi des études de mathématiques, nous allons nous rafraichir la mémoire. Prenez deux variables et , chacune étant un chiffre. Prenez ensuite le binôme qui représente un nombre à deux chiffres [9] .
- Le fait d’introduire la quantité fait du binôme un nombre à deux chiffres. Quelle que soit la valeur que vous attribuiez à , sera un nombre dont la dizaine sera A. Ainsi, si vaut 2 et , 6, alors vaut 26 [10] .
-
2Élevez ce binôme au cube. Vous le voyez, on expose le mécanisme à l’envers, puisqu’on commence par élever au cube, le but étant de comprendre comment la technique de la première étape fonctionne. Il faut donc développer qui peut s’écrire ainsi : . Il serait trop long d’expliquer le calcul, mais sachez que cette opération donne : [11] .
- Comme cela a été dit, il faut quelques connaissances en algèbre et en arithmétique. Il est également possible de servir du triangle de Pascal et de la formule qui en découle.
-
3Comprenez le fonctionnement de cet algorithme fondé sur la division. Trouver une racine cubique, c’est principalement faire des divisions en cascade. Le principe d’une division est de trouver deux facteurs qui, multipliés entre eux, donnent le nombre de départ. Quand vous recherchez une racine cubique, vous vous donnez comme objectif de trouver le facteur, ici 10A + B, qui, élevé au cube, vous donne le nombre de départ. En fait, ces deux valeurs que sont A et B ne sont pas significatives pour le calcul numérique, mais elles servent littéralement pour comprendre l’algorithme utilisé plus haut [12] .
-
4Analysez la structure du binôme développé. Quand vous décomposez le polynôme de développement, vous commencez à comprendre comment fonctionne l’algorithme dont vous vous êtes servi. Remarquez qu’à chaque étape, le diviseur est la somme (un peu compliquée, certes !) de quatre termes différents les uns des autres et qui sont le résultat d’opérations précises. Ces termes en question méritent d’être précisés [13] .
- Le coefficient du premier terme du binôme est 1 000, parce qu’on a décidé d’élever un nombre à deux chiffres. En fait, la première étape du calcul de la racine consiste à trouver la valeur qui, élevée au cube, est inférieure à la valeur de départ. Si cette dernière est un nombre, vous n’oublierez pas de multiplier par 1 000 pour satisfaire à .
- Le coefficient du deuxième terme du binôme est 300. Cette valeur est obtenue par l’opération . Souvenez-vous : dans le calcul de la racine cubique, la première composante du diviseur est toujours multipliée par 300.
- La deuxième composante du diviseur s’explique par le troisième terme du polynôme de développement, lequel se présente littéralement sous la forme 30AB2.
- Quant à la troisième composante du diviseur, c’est le dernier terme du polynôme de développement, lequel se présente littéralement sous la forme B3.
-
5Regardez comment augmente la précision de la racine. Chaque fois que vous mettez en œuvre l’algorithme, vous obtenez une racine cubique plus précise. Nous avions pris l’exemple de la recherche de la racine cubique de 10. Après la première application de l’algorithme, nous avions trouvé comme racine provisoire 2, car est proche de 10, mais inférieure. Après la deuxième série de calculs, vous avez obtenu 2,1. Après élévation au cube (), vous avez une valeur bien plus proche du 10 que vous recherchez. Après la troisième série de calcul, vous avez trouvé 2,15, qui, élevé au cube, donne : . En abaissant après chaque étape un groupe de trois chiffres, vous affinez votre résultat [14] .Publicité
Conseils
- Comme souvent en mathématiques, c’est en pratiquant que vous vous améliorerez. Plus vous ferez d’exercices, mieux vous comprendrez et plus vite vous irez.
Avertissements
- Il est très facile de faire des erreurs de calcul, c’est pourquoi il faut toujours vérifier ses calculs et voir si la réponse est cohérente.
Éléments nécessaires
- Un crayon ou un stylo
- Du papier
- Une règle
- Une gomme
Références
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
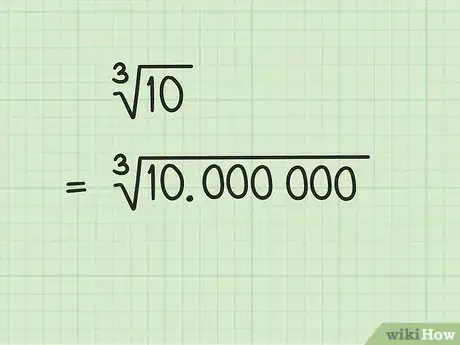
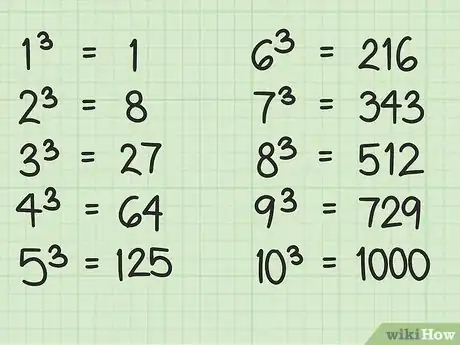










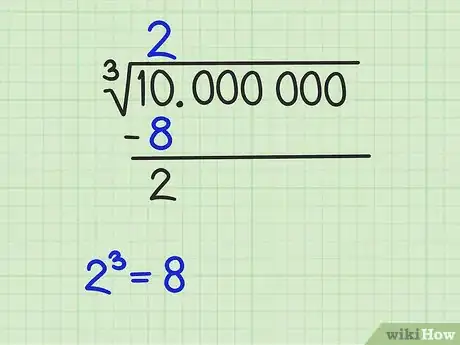

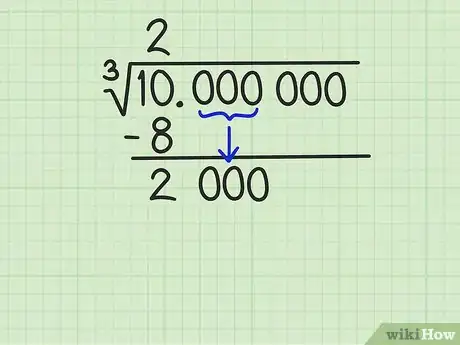
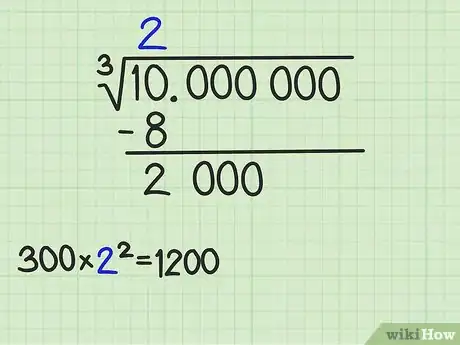

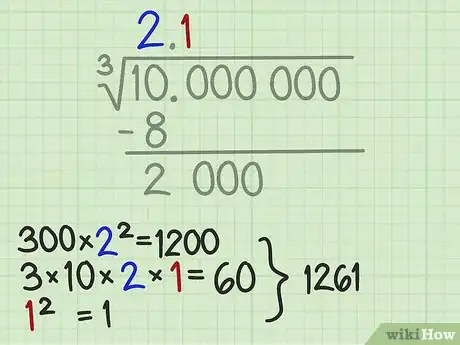
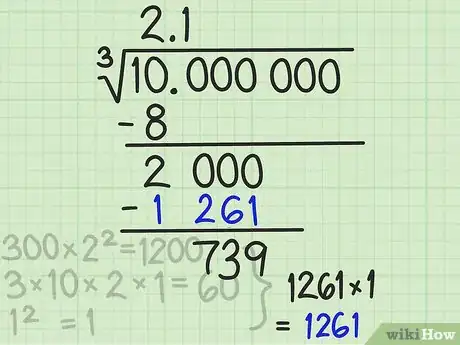
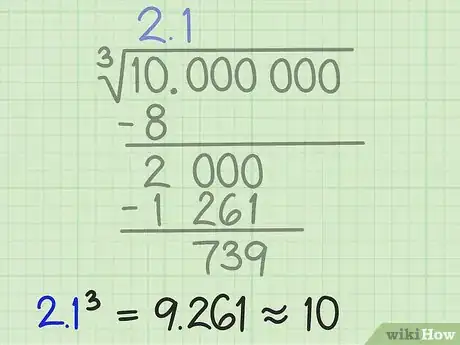







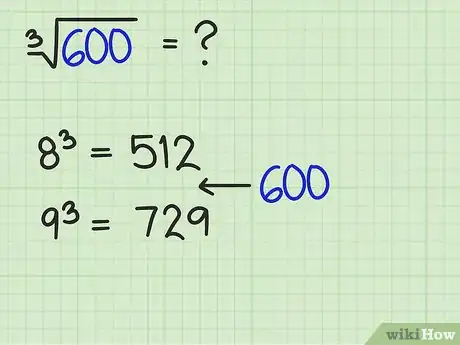


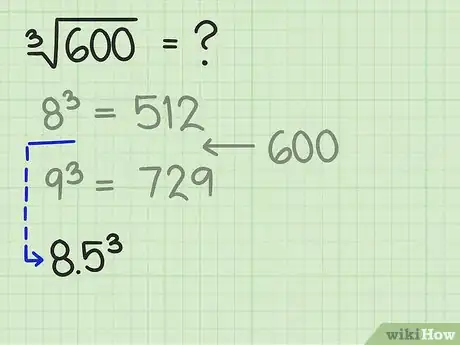
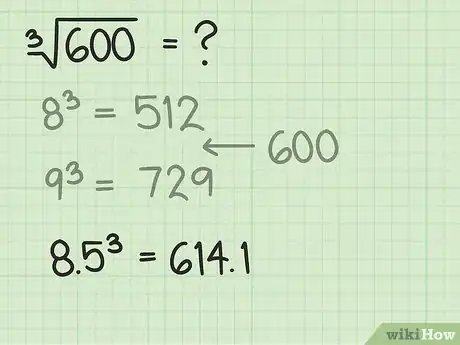

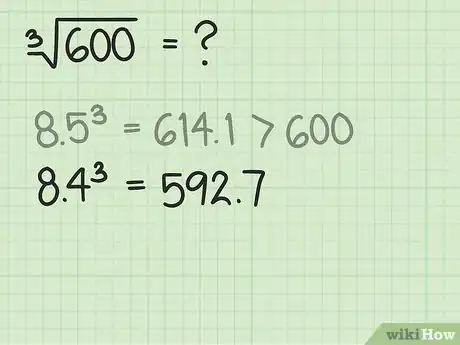


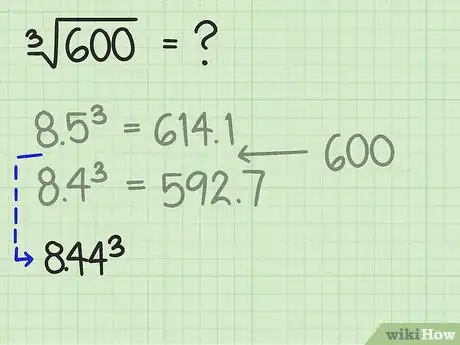


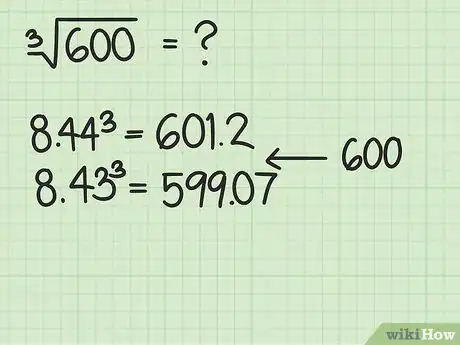













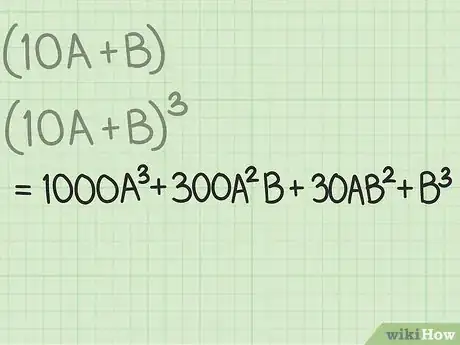


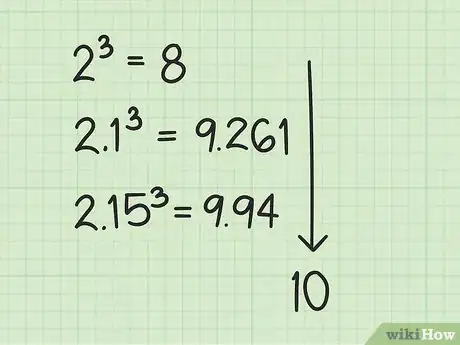





















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 20 565 fois.