Comment calculer une vitesse moyenne

Coécrit par l'équipe de wikiHow

Calculer une vitesse moyenne est assez simple, puisqu’il suffit de diviser la distance parcourue par le temps de parcours, soit ${\text{vitesse}}={\frac {\text{distance}}{\text{temps}}}$ . Cependant, il arrive que les vitesses, les distances parcourues et les temps de parcours varient lors d’un trajet, ce qui fait qu’il faut utiliser des formules différentes pour calculer des vitesses moyennes. Dans notre civilisation, dans laquelle le temps est souvent compté, il est très utile de savoir faire ces différents calculs pour ne pas se mettre en retard et être à l’heure à ses rendez-vous.

Méthode 1

Méthode 1 sur 5:
Calculer une vitesse moyenne classique

1
Repérez les informations données dans l'exercice. Pour utiliser cette méthode, vous devez connaitre :
- la distance totale parcourue par une personne ou un véhicule,
- le temps mis par la personne ou le véhicule pour couvrir cette distance,
- exercice : Pierre a parcouru 150 kilomètres en 3 heures, quelle a été sa vitesse moyenne ?
2
Inscrivez et retenez la formule de calcul de la vitesse. Elle se présente ainsi : $V={\frac {D}{T}}$ , dans laquelle $V$ est la vitesse moyenne, $D$ , la distance parcourue, $T$ , le temps de parcours ^{[1]
X
Source de recherche}.
3
Indiquez la distance dans la formule. Elle est représentée dans cette dernière par la variable $D$ $D$ .
- Ainsi, si Pierre parcourt 150 kilomètres, votre formule se présente ainsi : $V={\frac {150}{T}}$ .
4
Indiquez le temps de parcours dans la formule. Elle est représentée dans cette dernière par la variable $T$ $T$ .
- Ainsi, si Pierre roule pendant 3 heures, votre formule se présente ainsi : $V={\frac {150}{3}}$ .
5
Divisez la distance par le temps de parcours. Vous aurez ainsi une vitesse moyenne par unité de temps, ici en une heure.
- Pour reprendre notre exemple, nous avons donc :
  $V={\frac {150}{3}}$
  
  $V=50$
  Pierre, qui a parcouru 150 kilomètres en 3 heures, a roulé à une vitesse moyenne de 50 km/h.
Publicité

Méthode 2

Méthode 2 sur 5:
Calculer une vitesse moyenne sur des tronçons (1er cas)

1
Repérez les informations données dans l'exercice. Pour utiliser cette méthode, vous devez connaitre :
- les distances parcourues pour chacun des tronçons,
- le temps de parcours de chacun de ces tronçons ^{[2]
  X
  Source de recherche},
- exercice : Pierre a parcouru un premier tronçon de 150 kilomètres en 3 heures, puis un deuxième de 120 kilomètres en 2 heures, et enfin, un dernier de 70 kilomètres en 1 heure, quelle a été sa vitesse moyenne sur l'ensemble du parcours ?
2
Inscrivez et retenez la formule de calcul de la vitesse. Elle se présente ainsi : $V={\frac {D}{T}}$ , dans laquelle $V$ est la vitesse moyenne, $D$ , la distance parcourue, $T$ , le temps de parcours ^{[3]
X
Source de recherche}.
3
Déterminez la distance parcourue. Pour l'obtenir, vous devez faire la somme des longueurs (en km) des différents tronçons. Le résultat obtenu viendra remplacer dans la formule la variable $D$ $D$ .
- Ainsi, si Pierre a parcouru 150 kilomètres, puis 120 kilomètres et encore 70 kilomètres, il vous suffit d’additionner les longueurs des trois tronçons, ce qui donne : $150+120+70=340\ km$ . Votre formule de la vitesse moyenne se présente alors ainsi : $V={\frac {340}{T}}$ .
4
Déterminez le temps de parcours. Faites la somme des temps de parcours des différents tronçons. Ce résultat se substituera dans la formule à la variable $T$ $T$ .
- Pierre a donc roulé 3 heures, puis 2 heures et enfin, 1 heure. Additionnez simplement ces trois durées, ce qui donne : $3+2+1=6\ h$ . Votre formule se présente alors ainsi : $V={\frac {340}{6}}$ .
5
Divisez la distance parcourue par le temps de parcours. Vous obtiendrez ainsi la vitesse moyenne sur l’ensemble du parcours.
- Pour reprendre notre exemple, nous avons donc :
  $V={\frac {340}{6}}$
  
  $V=56,67$
  Pierre a donc parcouru 150 kilomètres en 3 heures, puis 120 kilomètres en 2 heures, et enfin 70 kilomètres en 1 heure, sa vitesse moyenne sur l’ensemble du parcours a été d’environ 57 km/h.
Publicité

Méthode 3

Méthode 3 sur 5:
Calculer une vitesse moyenne sur des tronçons (2e cas)

1
Repérez les informations données dans l'exercice. Pour utiliser cette méthode, vous devez connaitre :
- les vitesses observées sur les différents tronçons du parcours,
- la durée de conduite (en heures, par exemple) sur chacun des tronçons ^{[4]
  X
  Source de recherche},
- exercice : Pierre a parcouru un premier tronçon à 50 km/h pendant 3 heures, puis un deuxième à 60 km/h dans les 2 heures suivantes, et enfin, un troisième à 70 km/h pendant la dernière heure. Quelle a été sa vitesse moyenne sur l'ensemble du parcours ?
2
Inscrivez et retenez la formule de calcul de la vitesse. Elle se présente ainsi : $V={\frac {D}{T}}$ , dans laquelle $V$ est la vitesse moyenne, $D$ , la distance parcourue, $T$ , le temps de parcours ^{[5]
X
Source de recherche}.
3
Déterminez la distance parcourue. Pour cela, vous devez multiplier chacune des vitesses par le temps de parcours du tronçon concerné. Vous obtiendrez ensuite les longueurs des différents tronçons. Vous les additionnerez et vous aurez la distance totale du trajet parcouru, valeur qui remplacera $D$ $D$ dans la formule.
- Dans notre exemple, nous avons :
  50 km/h pendant 3 heures, soit $50\times 3=150\ {\text{km}}$ ,
  60 km/h pendant 2 heures, soit $60\times 2=120\ {\text{km}}$ ,
  70 km/h pendant 1 heure, soit $70\times 1=70\ {\text{km}}$ ,
  ainsi, la distance totale parcourue est de : $150+120+70=340\ {\text{km}}.$ Après remplacement, votre formule se présente ainsi : $V={\frac {340}{T}}$ .
4
Déterminez le temps de parcours. Rien de plus simple : additionnez les temps de parcours de chacun des tronçons. Ce résultat viendra remplacer la variable $T$ $T$ dans la formule.
- Ainsi, Pierre a roulé 3 heures, puis 2 heures, et enfin, 1 heure. Vous additionnez toutes ces durées et vous obtenez : $3+2+1=6$ . Après remplacement, votre formule se présente ainsi : $V={\frac {340}{6}}$ .
5
Divisez la distance parcourue par le temps de parcours. Vous obtiendrez, en km/h, la vitesse moyenne.
- Pour reprendre notre exemple, nous avons :
  $V={\frac {340}{6}}$
  
  $V=56,67$
  Pierre a fait du 50 km/h pendant 3 heures, puis 60 km/h dans les 2 heures suivantes, et en fin du 70 km/h pendant la dernière heure : sur ce parcours, Pierre a roulé à une vitesse moyenne d’environ 57 km/h.
Publicité

Méthode 4

Méthode 4 sur 5:
Calculer une vitesse moyenne sur des tronçons (3e cas)

1
Repérez les informations données dans l'exercice. Pour utiliser cette méthode, vous devez connaitre :
- deux vitesses (ou plus),
- deux temps de parcours (ou plus) absolument identiques,
- exercice : Pierre a roulé à 40 km/h sur un premier tronçon pendant deux heures, puis à 60 km/h sur un second tronçon pendant les deux heures suivantes, quelle a été sa vitesse moyenne sur l'ensemble du parcours ?
2
Inscrivez la bonne formule. Lorsque vous avez deux temps de parcours identiques avec des vitesses différentes, la formule est la suivante : $V={\frac {v_{a}+v_{b}}{2}}$ $V={\frac {v_{a}+v_{b}}{2}}$ , dans laquelle $V$ $V$ est la vitesse moyenne, $v_{a}$ $v_{a}$ , la vitesse durant la première moitié du trajet et $v_{b}$ $v_{b}$ , celle de la seconde moitié du parcours ^{[6]
X
Source de recherche}.
- Dans ce type de problèmes, il importe peu de savoir quelle distance a été réellement parcourue pendant ce laps de temps. En fait, cette formule est une moyenne de vitesses moyennes.
- Cette formule peut se dériver à l’infini : tant que les durées de parcours sont identiques, vous pouvez additionner trois, quatre, dix… vitesses, le tout sera de diviser par le nombre de tronçons. La formule de calcul avec trois vitesses ( $v_{a},v_{b},v_{c}$ ) est la suivante : $V={\frac {v_{a}+v_{b}+v_{c}}{3}}$ et celle avec quatre vitesses ( $v_{a},v_{b},v_{c},v_{d}$ ), $V={\frac {v_{a}+v_{b}+v_{c}+v_{d}}{4}}$ .
3
Faites l’application numérique. Peu importe l’ordre des vitesses $v_{a}$ $v_{a}$ et $v_{b}$ $v_{b}$ , car l’addition est commutative, c'est-à-dire que $v_{a}+v_{b}=v_{b}+v_{a}$ $v_{a}+v_{b}=v_{b}+v_{a}$ .
- Ainsi, si la vitesse de la première partie est de 40 km/h, et celle de la seconde, de 60 km/h, la formule se présente ainsi : $V={\frac {40+60}{2}}$ .
4
Additionnez les deux vitesses. Divisez le résultat par 2 et vous obtiendrez ainsi la vitesse moyenne sur l'ensemble du parcours.
- Pour reprendre notre exemple, nous avons :
  $V={\frac {40+60}{2}}$
  
  $V={\frac {100}{2}}$
  
  $V=50$
  Pierre a roulé à 40 km/h pendant deux heures, puis à 60 km/h pendant les deux heures suivantes, sa vitesse moyenne a donc été de 50 km/h.
Publicité

Méthode 5

Méthode 5 sur 5:
Calculer une vitesse moyenne sur un aller-retour

1
Repérez les informations données dans l'exercice. Pour utiliser cette méthode, vous devez connaitre :
- un même parcours (un aller-retour, par exemple),
- une première vitesse pour l’aller et une seconde pour le retour,
- exercice : Pierre est allé à 160 kilomètres de chez lui à une vitesse de 40 km/h. Il est rentré le soir à 60 km/h, quelle a été sa vitesse moyenne sur l'ensemble du parcours ?
2
Inscrivez et retenez la formule à utiliser. Ici, vous avez une distance identique, mais deux vitesses différentes. La formule de calcul de la vitesse moyenne est la suivante : $V={\frac {2(v_{a})(v_{b})}{v_{a}+v_{b}}}$ $V={\frac {2(v_{a})(v_{b})}{v_{a}+v_{b}}}$ , dans laquelle $V$ $V$ est toujours la vitesse moyenne, $v_{a}$ $v_{a}$ , la vitesse à l’aller et $v_{b}$ $v_{b}$ , la vitesse observée au retour ^{[7]
X
Source de recherche}.
- Même si ce n’est pas systématique, cette formule s’applique plus particulièrement à des trajets allers-retours.
- Dans ce type de problèmes, il importe peu de savoir les temps de parcours des deux tronçons. En fait, le temps pourrait rentrer dans la formule théorique, mais il serait systématiquement supprimé par simplification de la fraction.
- Si vous aviez trois parcours identiques avec trois vitesses différentes, la formule serait : $V={\frac {3(v_{a})(v_{b})(v_{c})}{(v_{a}v_{b})+(v_{b}v_{c})+(v_{c}v_{a})}}$ ^{[8]
  X
  Source de recherche}.
3
Faites l’application numérique. Peu importe l’ordre des vitesses $v_{a}$ $v_{a}$ et $v_{b}$ $v_{b}$ , car l’addition et la multiplication sont commutatives.
- Ainsi, dans notre exemple, la première vitesse est de 40 km/h, la seconde, de 60 km/h, la formule se présente alors de la façon suivante :
  $V={\frac {(2)(40)(60)}{40+60}}$ .
4
Doublez le produit des deux vitesses. Ce résultat sera tout simplement le numérateur de votre fraction.
- Reprenons notre exemple :
  $V={\frac {(2)(40)(60)}{40+60}}$
  
  $V={\frac {4\ 800}{40+60}}$
5
Additionnez les deux vitesses. Ce résultat sera le dénominateur de votre fraction.
- Reprenons notre exemple :
  $V={\frac {4\ 800}{40+60}}$
  
  $V={\frac {4\ 800}{100}}$
6
Calculez la fraction. Ainsi, vous obtiendrez la vitesse moyenne sur l’ensemble du parcours.
- Reprenons notre exemple :
  $V={\frac {4\ 800}{100}}$
  
  $V=48$
  Pierre a roulé à l’aller à 40 km/h sur 160 kilomètres, puis est revenu le soir chez lui à une vitesse de 60 km/h : sa vitesse moyenne sur l’ensemble de son voyage a été de 48 km/h.
Publicité

wikiHows en relation

Publicité

Références

À propos de ce wikiHow

Coécrit par:

l'équipe de wikiHow

Rédacteurs de wikiHow

Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.

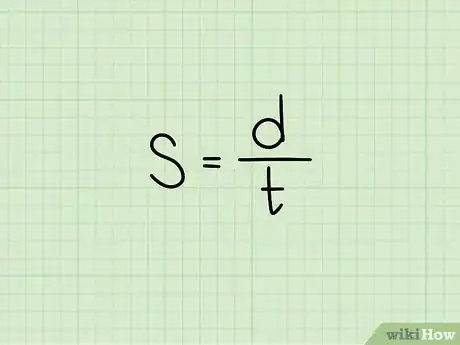
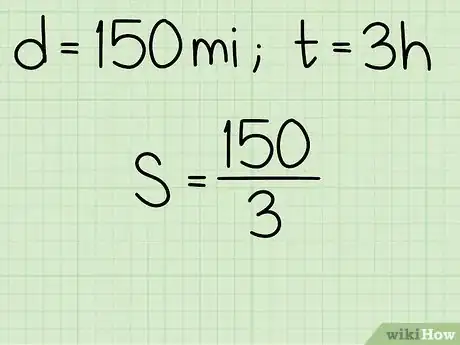
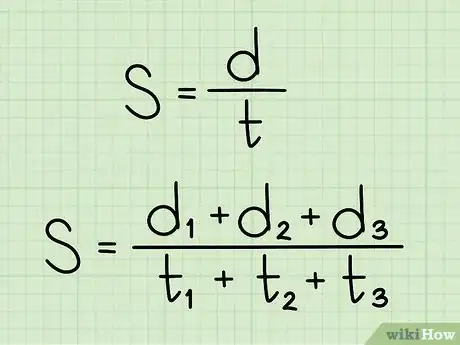
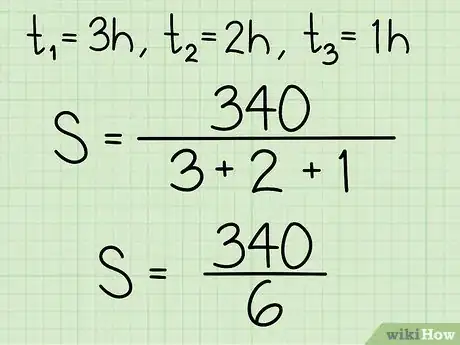
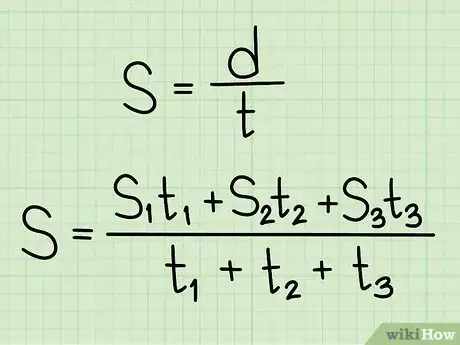
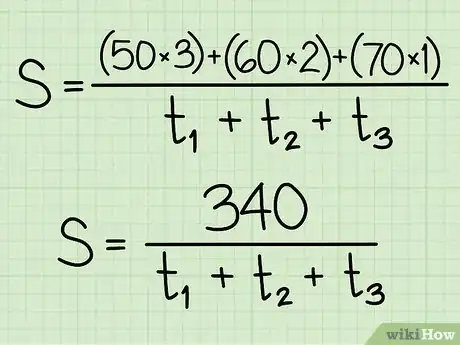
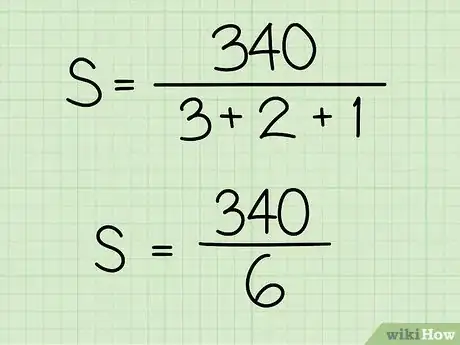
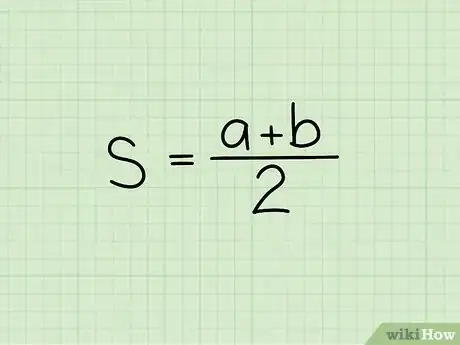
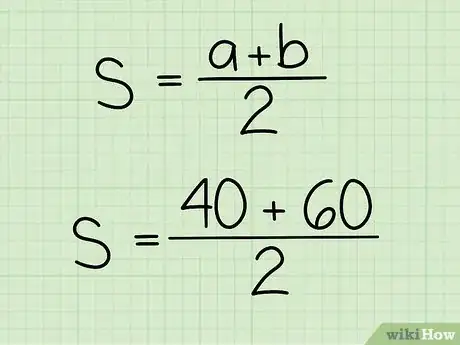
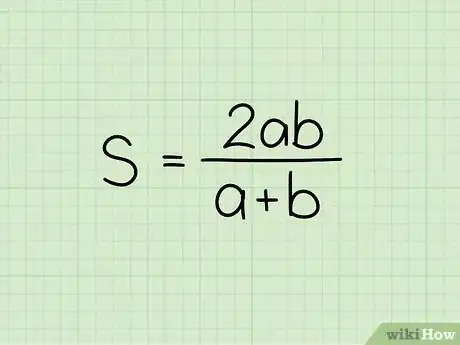
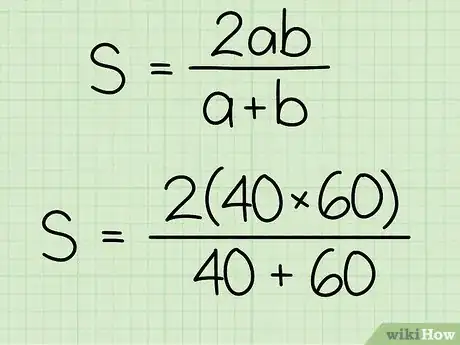
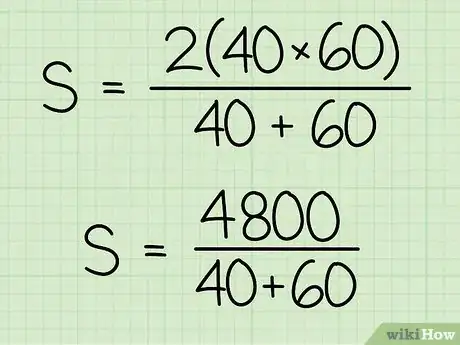
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 32 448 fois.

Catégories: Calculs

Publicité