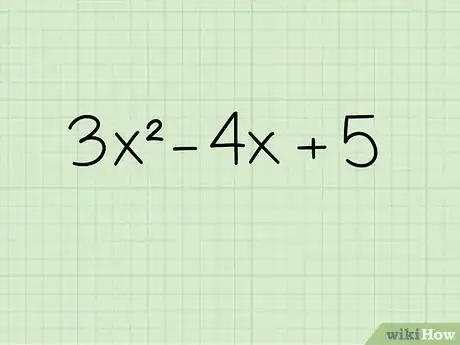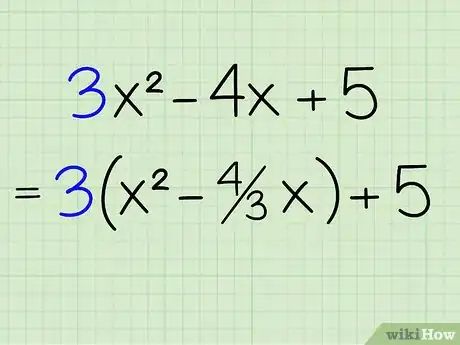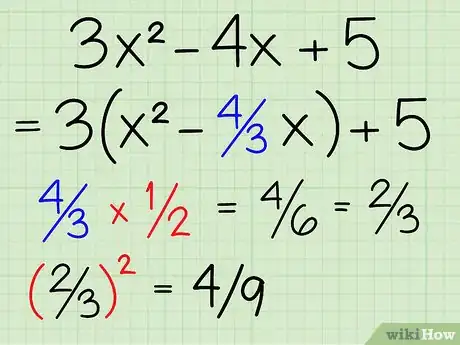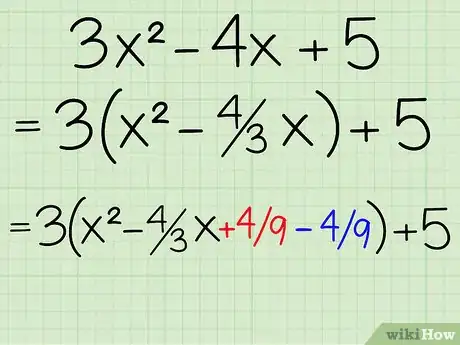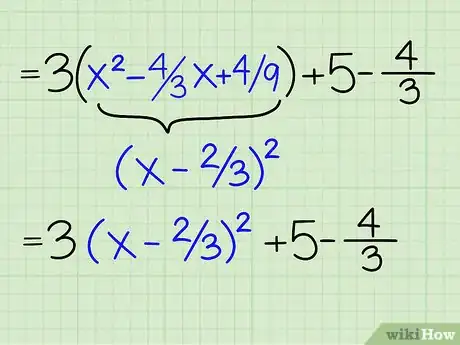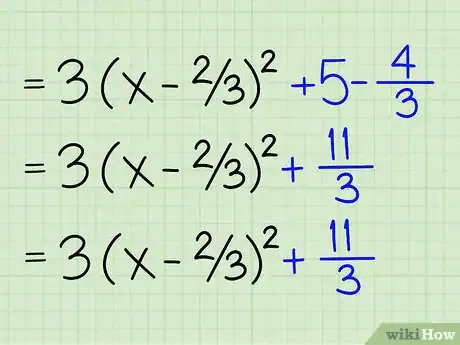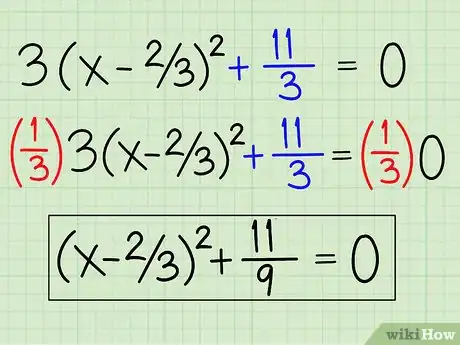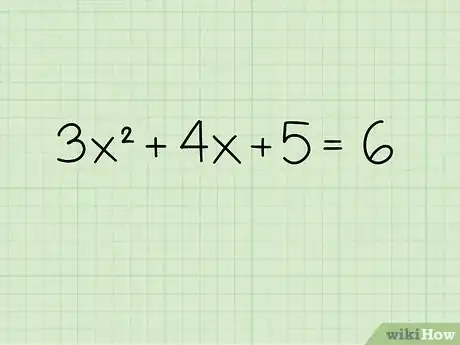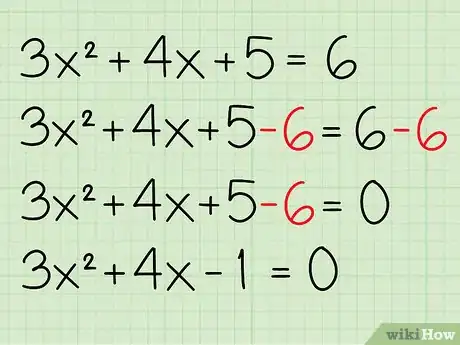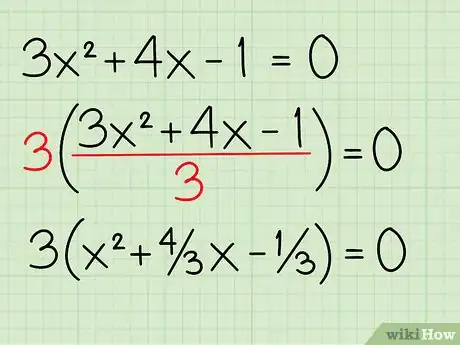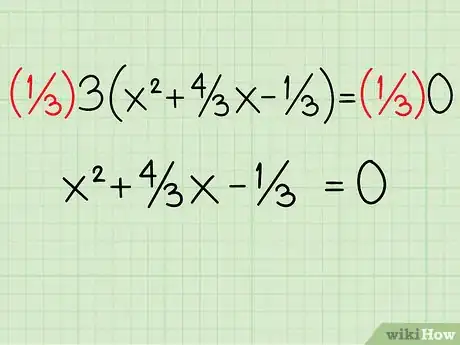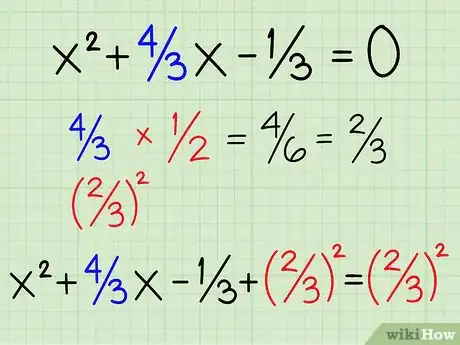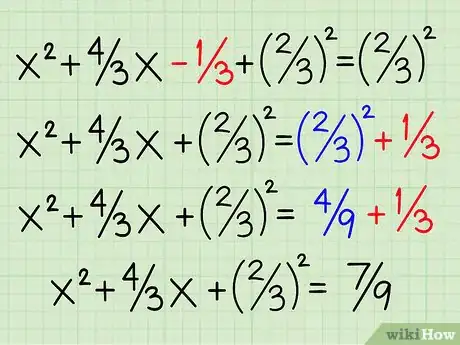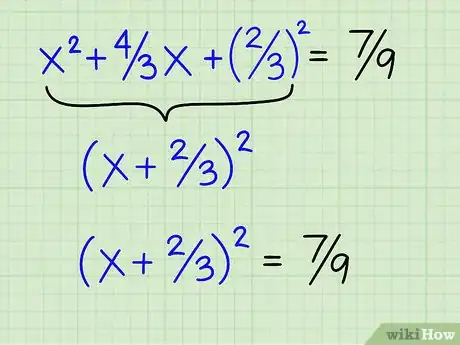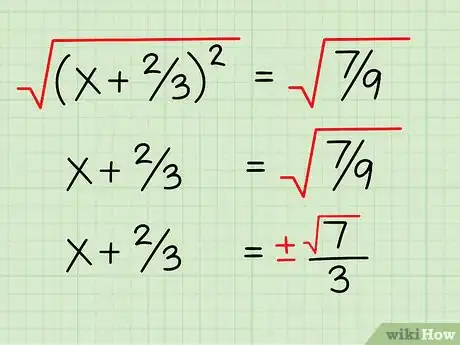Comment compléter le carré pour résoudre une équation

Informations concernant l'auteur.e

Il existe une méthode très pratique pour factoriser les équations du second degré, celle qui consiste à compléter le carré. En l'utilisant, on rend l'équation plus lisible et souvent plus facile à manipuler. On peut donc utiliser cette technique pour arranger une équation un peu complexe ou pour la résoudre.

Méthode 1

Méthode 1 sur 2:
Transformer l'équation sous forme de vertex

1
Posez bien l'équation. Nous allons prendre l'équation : 3x² - 4x + 5.
2
Mettez en facteur le coefficient de x² pour les deux premiers termes. Pour factoriser les deux premiers termes par 3, isolez ce chiffre et mettez entre parenthèses les deux termes, chacun divisé par 3. 3x² divisé par 3 donne x² et 4x divisé par 3 donne 4/3x. D'où la nouvelle équation : 3(x² - 4/3x) + 5. On laisse la constante 5 de côté pour les besoins du calcul.
3
Divisez le coefficient de x par 2 et élevez au carré. Prenez le coefficient du second terme, ici 4/3 (en théorie, on l'appelle b) et divisez-le par 2 : 4/3 ÷ 2 ou 4/3 x 1/2. Cela vous donne 4/6 ou 2/3. Puis, calculez le carré de 2/3, soit 4/9. Inscrivez ce résultat ^{[1]
X
Source de recherche}.
4
Ajoutez tout en soustrayant cette quantité à l'intérieur des parenthèses. Cette manipulation a pour but de factoriser sous la forme d'un carré parfait, les trois premiers termes. La démarche peut sembler bizarre, car on a en quelque sorte ajouté 0 ! Pourtant c'est nécessaire aux étapes qui suivent. La nouvelle équation est désormais celle-là : 3(x² - 4/3 x + 4/9 - 4/9) + 5 ^{[2]
X
Source de recherche}.
5
Sortez le terme négatif (qu'on vient de rajouter) de la parenthèse. Le problème est que -4/9 est dans la parenthèse. Il faut donc le multiplier par 3 : -4/9 x 3 = -12/9 ou -4/3. Si le coefficient de x de votre équation est différent de 1, sautez cette étape.
6
Factorisez sous la forme d'un carré parfait l'intérieur de la parenthèse. Maintenant, vous vous retrouvez avec cette partie d'équation : 3(x² -4/3x +4/9). On a trouvé la valeur qui complétait le carré, 4/9. On peut réécrire l'équation sous cette forme : 3(x - 2/3)². Pour trouver la constante du carré parfait, il faut prendre la moitié du coefficient de x. Ici, la moitié de 4/3, soit 4/6, soit 2/3. On vérifie si notre factorisation est correcte ^{[3]
X
Source de recherche} :
- 3(x - 2/3)² =
- 3(x - 2/3)(x -2/3) =
- 3[(x² -2/3x -2/3x + 4/9)]
- 3(x² - 4/3x + 4/9)
7
Calculez les constantes. Passez maintenant aux constantes que vous avez laissées de côté. Dans notre cas, on a deux constantes (termes sans inconnue). L'équation transformée est celle-ci : 3(x - 2/3)² - 4/3 + 5. Additionnez -4/3 et 5, ce qui équivaut à 11/3. On obtient ce résultat en réduisant les deux nombres au même dénominateur : -4/3 et 15/3 (=5/1 x 3/3), on ajoute 15-4, soit 11, d'où le 11/3.
- -4/3 + 15/3 = 11/3.
8
Écrivez l'équation sous forme de vertex. Voilà ! c'est fini ! L'équation finale est donc : 3(x - 2/3)² + 11/3. Vous pouvez supprimer le 3 en divisant tout par 3 et on obtient alors : (x - 2/3)² + 11/9. Vous avez réussi à mettre l'équation sous forme de vertex du type : a(x - h)² + k, où k représente la constante.

Publicité

Méthode 2

Méthode 2 sur 2:
Résoudre une équation du second degré

1
Posez bien le problème. Nous allons prendre l'équation : 3x² + 4x + 5 = 6.
2
Regroupez toutes les constantes dans le membre de gauche. Par constante, on entend tout terme qui n'est pas relié à une inconnue, en somme des nombres. Dans notre exemple, on à 5 à gauche et 6 à droite. On déplace 6 à gauche en soustrayant 6 des deux côtés. On obtient ainsi 0 à droite (6-6) et -1 à gauche (5-6). L'équation est désormais la suivante : 3x² + 4x - 1 = 0 ^{[4]
X
Source de recherche}.
3
Mettez en facteur le coefficient de x². Dans notre cas, on met 3 en facteur et on divise donc chaque terme par 3. On obtient : 3x² ÷ 3 = x², 4x ÷ 3 = 4/3x et 1 ÷ 3 = 1/3. Au final, l'équation devient : 3(x² + 4/3x - 1/3) = 0.
4
Divisez l'équation par la valeur qu'on vient de mettre en facteur. Divisez les deux membres de l'équation par 3. On obtient alors : x² + 4/3x - 1/3 = 0.
5
Divisez le coefficient de x par 2 et élevez au carré. Prenez le coefficient du second terme, ici 4/3 (en théorie, on l'appelle b) et divisez-le par 2 : 4/3 ÷ 2 ou 4/3 x 1/2. Cela vous donne 4/6 ou 2/3. Puis, calculez le carré de 2/3, soit 4/9. Ajoutez ce résultat aux deux membres de l'équation. La nouvelle équation est désormais : x² + 4/3 x + 2/3² - 1/3 = 2/3².
6
Passez la constante de gauche à droite et faites le calcul. Passez le « -1/3 » de droite à gauche. Il suffit de changer son signe, soit 1/3 (x² + 4/3 x + 2/3² = 4/9 + 1/3). Additionnez 4/9 et 1/3. Les dénominateurs étant différents, il faut en trouver un commun. Ici, c'est facile : il faut tout ramener sur 9. On multiplie 1/3 x 3/3 = 3/9. Additionnez 3/9 et 4/9, ce qui donne 7/9 à droite. L'équation se présente ainsi : x² + 4/3 x + 2/3² = 7/9.
7
Transformez le membre de gauche en un carré parfait. Avec le calcul de la valeur de complément du carré (4/9), le plus dur est fait. Il ne reste plus qu'à reformuler l'équation sous la forme : x + moitié du coefficient de x, le tout au carré, soit : (x + 2/3)². Si on développe, on obtient bien notre équation : x² + 4/3 x + 4/9. Tout est parfait ! L'équation finale est donc : (x + 2/3)² = 7/9.
8
Prenez la racine carrée des deux membres. La racine carrée de (x + 2/3)² est tout simplement x + 2/3. À droite, on a +/- (√ 7)/3. La racine du dénominateur, 9, est 3 et le numérateur reste sous la forme √ 7. Souvenez-vous que la racine d'un nombre peut être positive ou négative !
9
Isolez l'inconnue. Pour ce faire, passez la constante (2/3) à droite en changeant son signe. Vous voilà avec vos deux solutions : +/- (√ 7)/3 - 2/3. Vous pouvez les laisser sous cette forme ou faire le calcul approché.

Publicité

Conseils

N'oubliez pas qu'il y a toujours deux réponses, l'une positive, l'autre négative !
Cette méthode, pas si simple, se doit d'être pratiquée régulièrement si vous ne voulez pas en oublier les principes. Entrainez-vous !
Retenez simplement que le chiffre $2$ dans la formule du binôme à l'ordre 2 $(x\pm b)^{2}=x^{2}\pm 2*b*x+b^{2}$ indique la démarche à suivre pour résoudre l'équation du second degré.