Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 61 298 fois.
Au cours du temps, les hommes ont mis au point diverses méthodes de numération, la plus connue est la numération décimale (base 10). Il existe une base très utilisée en informatique depuis une cinquantaine d’années : la numération binaire (base 2). Même si c’est déroutant au départ, il est facile de compter en base 2 et de transformer un nombre binaire en un nombre décimal.
Table de conversion
|
Décimal |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Binaire |
0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
Étapes
Méthode 1
Méthode 1 sur 2:Apprendre la numération binaire
-
1Comprenez ce qu’est la numération binaire. Dans la vie quotidienne, nous utilisons des nombres décimaux (base 10). Tous les nombres s’écrivent avec des chiffres allant de 0 à 9. En système binaire, tous les nombres s’écrivent avec deux seuls chiffres : 0 et 1.
-
2Ajoutez 1 en remplaçant le dernier 0 en 1. Si un nombre binaire se termine par 0, lui ajouter 1 consiste simplement à remplacer le 0 par le 1 en question. C’est ainsi que les deux premiers chiffres en système binaire sont :
- 0 = zéro,
- 1 = un,
- pour ajouter 1 à un grand nombre binaire, laissez de côté tous les chiffres de gauche, sauf le dernier. C’est ainsi qu’en base 2, 1010 + 1 = 1011.
-
3Ajoutez 1 à un nombre binaire ne contenant que des 1. Dans notre exemple, nous en sommes arrivés à 1 et vous savez qu’en numération binaire, il n’y a pas de 2. Donc, vous devez passer à un nombre à deux chiffres. Mettez 1 à gauche et transformez le précédent 1 en 0 :
- 0 = zéro,
- 1 = un,
- 10 = deux,
- vous agissez de la même façon qu’en système décimal quand vous arrivez à 9 : vous repartez avec une dizaine (9 + 1 = 10). Les nombres binaires atteignent très vite une longueur importante.
-
4Utilisez ces règles pour compter jusqu’à cinq. Pour cela, il vous suffit d’appliquer les règles expliquées précédemment. Essayez d’abord sans regarder les solutions ci-dessous.
- 0 = zéro
- 1 = un
- 10 = deux
- 11 = trois
- 100 = quatre
- 101 = cinq
-
5Comptez jusqu’à 6. Il suffit donc de faire 5 + 1 (base 10) ou si vous préférez 101 + 1 (base 2). Concentrez-vous sur le dernier chiffre (le 1 de 101) et ajoutez-lui 1, ce qui fait 2, mais en base 2, c’est 10 (01 + 1 = 10). Remettez le 1 des centaines, ce qui donne :
- 110 = six
-
6Comptez jusqu’à dix. Appliquez tout ce que vous avez appris précédemment. Essayez d’abord sans regarder les solutions ci-dessous :
- 110 = six
- 111 = sept
- 1000 = huit
- 1001 = neuf
- 1010 = dix
-
7Observez le résultat d’une addition en base 2. Ne trouvez-vous pas originale la façon d’écrire 10 en base 2 ? C’est 1010. Huit (1000 en base 2) est un chiffre important, car il est égal à : 2 x 2 x 2, le nombre de zéros en base 2 est égal au nombre de fois où l’on multiplie par 2. Il en va de même de 16 (2 x 2 x 2 x 2, soit 4 zéros) qui s’écrit 10000 en base 2, et de 32 qui s’écrit 100000 (2 x 2 x 2 x 2 x 2).
-
8Exercez-vous avec des nombres plus grands. Ne vous affolez jamais, prenez le temps de bien décomposer et ayez en mémoire toutes les règles. Vous trouverez ci-dessous quelques additions que vous pouvez faire sans regarder la solution tout de suite.
- 12 + 1 = 1100 + 1 = 1101 (0 + 1 = 1, les autres chiffres ne sont pas modifiés).
- 15 + 1 = 1111 + 1 = 10000 = 16 (comme 1 + 1 = 2, il faut de nouveau rajouter un 1 à gauche et tous les chiffres deviennent des zéros).
- 45 + 1 = 101101 + 1 = 101110 = 46 (nous avons vu précédemment que 01 + 1 = 10, les autres chiffres ne sont pas modifiés).
Publicité
Méthode 2
Méthode 2 sur 2:Convertir un nombre binaire en nombre décimal
-
1Indiquez la valeur de chaque rang en base 2. À l'école, votre instituteur vous a enseigné la valeur des rangs : les unités, les dizaines, les centaines… Comme il n’y a que deux chiffres en base 2, chaque rang d’un nombre a une valeur double du rang précédent (à droite).
- 1 est l'unité
- 10 est la dizaine
- 100 est la centaine
- 1000 est le millier
-
2Multipliez chaque chiffre par la valeur de son rang. Commencez toujours par le chiffre (0 ou 1) le plus à droite et multipliez-le par 1. Sur la ligne suivante, inscrivez le chiffre qui se trouve juste à gauche du premier et multipliez-le par 2. Continuez ainsi en multipliant chaque fois par un multiple de 2.
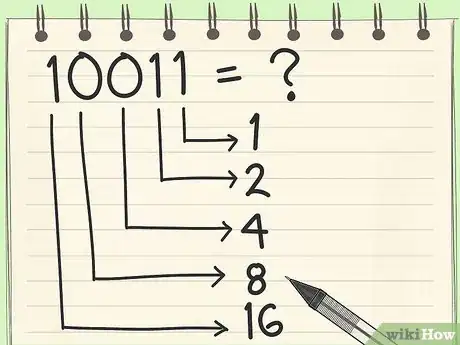
- Quelle est la valeur en système décimal du nombre binaire 10011 ?
- Le chiffre le plus à droite est 1. Vous multipliez le chiffre par 1 : 1 x 1 = 1.
- Le chiffre immédiatement à gauche est aussi 1. Multipliez-le par 2 : 1 x 2 = 2.
- Le chiffre suivant est 0. Multipliez-le par 4 : 0 x 4 = 0.
- Le chiffre encore plus à gauche est aussi 0. Multipliez-le par 8 : 0 x 8 = 0.
- Enfin, le chiffre le plus à gauche est 1. Multipliez-le par 16 : 1 x 16 = 16.
-
3Additionnez les produits obtenus. Chaque chiffre du nombre binaire a été converti en valeur décimale. Additionnez tous les résultats obtenus précédemment, ce qui donne :
- 1 + 2 + 0 + 0 + 16 = 19,
- ainsi, 10011 est la transcription en système binaire du nombre décimal 19.
Publicité
Conseils
- Il est possible de compter en système binaire sur ses doigts. Chaque doigt est un chiffre : si le doigt est allongé, ce sera « 1 », s’il est replié, ce sera « 0 [1] ».

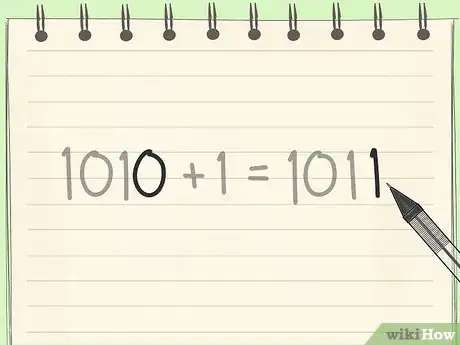
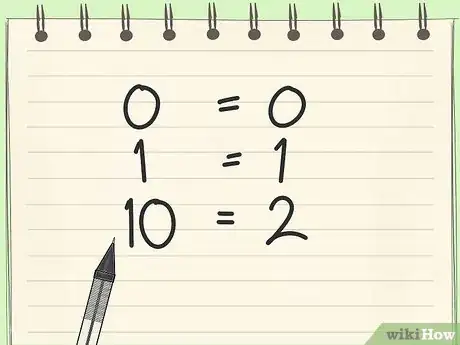



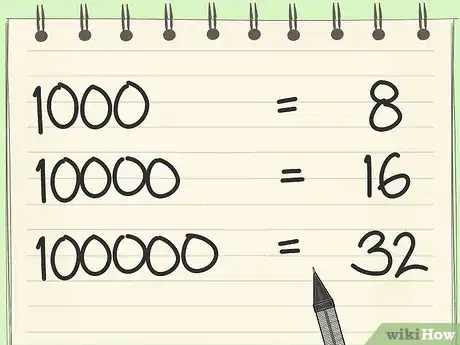
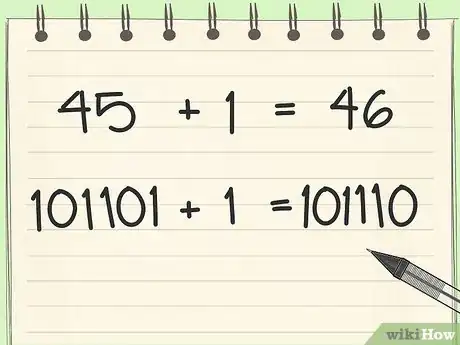
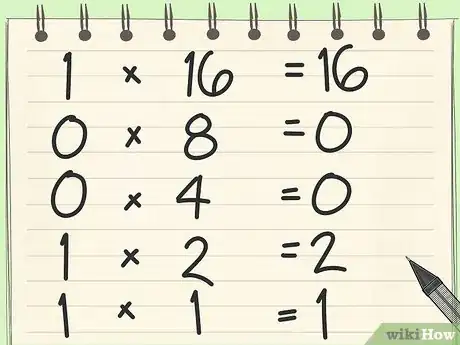
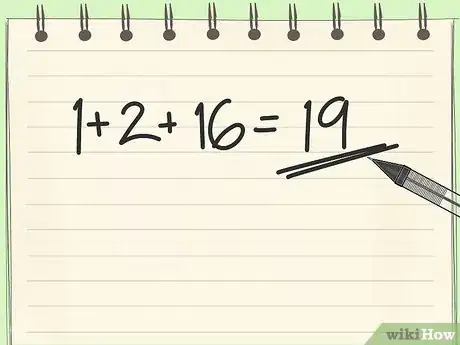



















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 61 298 fois.