Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 16 219 fois.
Les décimales périodiques, également appelées décimales récurrentes, sont des nombres décimaux qui ont un ou plusieurs chiffres qui se répètent indéfiniment à intervalles réguliers. Travailler avec des décimales périodiques peut parfois prêter à confusion, mais vous pouvez les transformer en fractions. Ces nombres sont parfois représentés par une ligne au-dessus des chiffres répétés. Par exemple, le nombre 3,7777 dans lequel le 7 est répété peut également être écrit comme ceci 3,7. Pour convertir un tel nombre en fraction, vous devez l’écrire sous forme d’une équation, faire une multiplication et une soustraction afin de supprimer la partie décimale qui est répétée et enfin résoudre l’équation.
Étapes
Partie 1
Partie 1 sur 2:Convertir les décimales périodiques de base
-
1Identifiez la décimale répétitive. Par exemple, dans le nombre 0,4444, la décimale répétitive est 4. Il s’agit d’une décimale périodique de base dans le sens où il n’y a pas de partie du nombre décimal qui ne se répète pas. Comptez le nombre de chiffres périodiques qu’il y a dans la suite.
- Une fois que vous avez écrit l’équation, vous devez la multiplier par 10y, où y correspond au nombre de chiffres qui sont répétés dans la suite [1] .
- Dans l’exemple de 0,4444, il n’y a qu’un seul chiffre qui est répété, par conséquent, vous devez multiplier l’équation par 101.
- Par exemple, si le nombre décimal périodique est 0,4545, il y a deux chiffres récurrents. Dans ce cas, vous devez multiplier l’équation par 102.
- Si les chiffres répétés sont trois, vous devez multiplier par 103 et ainsi de suite.
-
2Réécrivez le nombre décimal sous forme d’équation. Écrivez-le pour que x soit égal au nombre initial [2] . Dans ce cas, l’équation est x = 0,4444. Comme il n’y a qu’un seul chiffre décimal périodique, multipliez l’équation par 101 (ce qui équivaut à 10) [3] .
- Dans l’exemple où x = 0,4444, alors 10x = 4,4444.
- Dans l’exemple où x = 0,4545, il y a deux chiffres récurrents. Par conséquent, vous devez multiplier les deux côtés de l’équation par 102 (ce qui est égal à 100), ce qui donne 100x = 45,4545.
-
3Supprimez les décimales périodiques. Pour le faire, il suffit de soustraire x de 10x. Souvenez-vous que tout ce que vous faites d’un côté de l’équation doit également être fait dans l’autre. Par conséquent, nous avons [4] :
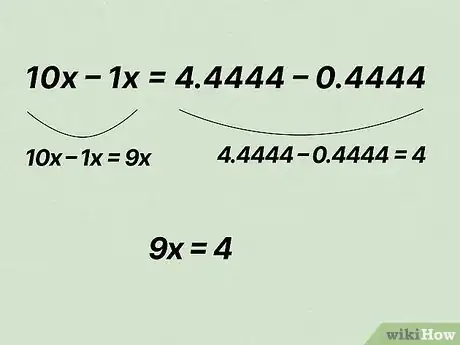
- 10x – 1x = 4,4444 – 0,4444
- à gauche, vous aurez 10x - 1x = 9x et à droite, vous aurez : 4,4444 – 0,4444 = 4
- ce qui donne 9x = 4
-
4Résolvez l’équation pour trouver la valeur de x. Une fois que vous connaissez la réponse que donne 9x, vous pouvez déterminer la valeur de x en divisant par 9 les deux parties de l’équation.
- À gauche de l’équation, vous aurez 9x ÷ 9 = x. À droite, vous obtiendrez 4/9.
- Par conséquent, x = 4/9 et le nombre périodique décimal 0,4444 peuvent s’écrire sous forme de la fraction 4/9.
-
5Simplifiez la fraction. Réécrivez-la dans sa forme la plus simple (si nécessaire) en divisant le dénominateur et le numérateur par le plus grand facteur commun [5] .
- Dans l’exemple du 4/9, la fraction est déjà exprimée dans sa forme la plus simple.
Publicité
Partie 2
Partie 2 sur 2:Convertir des nombres avec des décimales répétitives et non répétitives
-
1Identifiez les chiffres périodiques. Il n’est pas rare de trouver des nombres qui ont des chiffres non périodiques avant les décimales répétitives. Ceux-ci peuvent également être convertis en fractions.
- Prenez par exemple en compte le nombre 6,21515. Dans ce cas, 6,2 est non périodique et 15 est répétitif.
- Une fois encore, prenez note du nombre de chiffres qu’il y a dans la suite, car vous devriez effectuer une multiplication par 10y en vous basant sur ce nombre.
- Dans ce cas, il existe deux chiffres périodiques et pour cela, vous allez multiplier l’équation par 102.
-
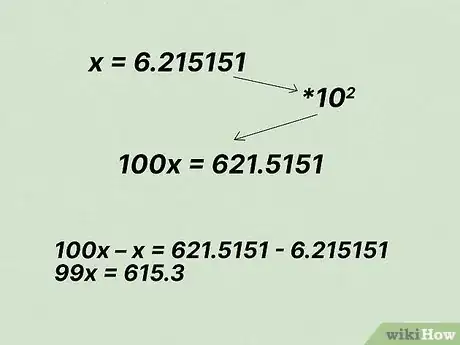
2Écrivez le problème sous forme d’équation. Ensuite, soustrayez les décimales périodiques. Une fois encore, si x = 6,215151 alors 100x = 621,515. Pour éliminer les décimales périodiques, supprimez-les des deux côtés de l’équation :
- 100x – x (= 99x) = 621,5151 – 6,215151 (= 615,3)
- par conséquent, 99x = 615,3
-
3Résolvez l’équation pour trouver la valeur de x. Étant donné que 99x = 615,3, divisez les deux côtés de l’équation par 99. Cela vous donne : x = 615,3/99.
-
4Supprimez les décimales du numérateur. Pour faire cela, il faut multiplier le numérateur et le dénominateur par 10z, avec z qui est égal au nombre de décimales que vous devez déplacer pour enlever la virgule. Dans 615,3 vous devez déplacer la virgule d’une seule position vers la droite, ce qui signifie que vous devez multiplier le numérateur et le dénominateur par 101.
- 615,3 x 10 / 99 x 10 = 6153/990.
- Simplifiez la fraction en divisant le dénominateur et le numérateur par le plus grand facteur commun (qui est 3 dans cet exemple). Ainsi, le résultat final est :
x = 2051/330.
Publicité
Références
- ↑ http://www.virtualnerd.com/tutorials/?id=PreAlg_05_01_0037
- ↑ http://www.basic-mathematics.com/converting-repeating-decimals-to-fractions.html
- ↑ https://www.khanacademy.org/math/algebra/alg-1-old-content/conv_rep_decimals/v/coverting-repeating-decimals-to-fractions-1
- ↑ http://www.virtualnerd.com/tutorials/?id=PreAlg_05_01_0037
- ↑ https://www.khanacademy.org/math/algebra/alg-1-old-content/conv_rep_decimals/v/coverting-repeating-decimals-to-fractions-2


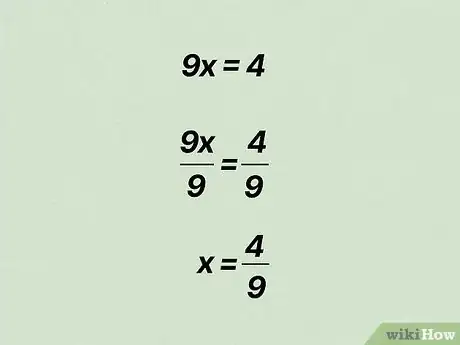























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 16 219 fois.