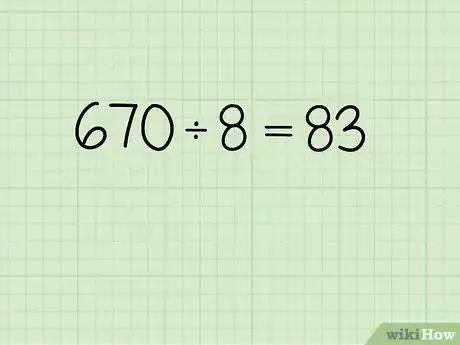Comment convertir un nombre en base 10 en un nombre en base 8

Le système de numération octal, de base 8, ne comprend que des nombres composés des chiffres de 0 à 7. C’est un système qui peut paraitre exotique en comparaison du système en base 10 utilisé tous les jours, mais il présente l’avantage de faciliter le passage à la base 2, celle utilisée en informatique. En effet, chaque chiffre en base 8 n’a qu’une seule conversion à trois chiffres en binaire [1] . Le passage de la base 10 à la base 8 est loin d’être intuitif, mais si vous savez faire une division, alors vous saurez convertir en base 8. Deux méthodes sont possibles, celle de la division et celles des restes. La première, plus longue, permet de mieux comprendre les mécanismes, la seconde, plus rapide, est plus difficile à comprendre.

Méthode 1
Méthode 1 sur 2:
Convertir en base 8 en divisant

  1. Image intitulée Convert from Decimal to Octal Step 1
    1
    Utilisez cette méthode pour comprendre la conversion. Des deux méthodes proposées dans cet article, celle-ci est la plus simple à assimiler. Si vous avez l’habitude de travailler avec d’autres bases numériques, la seconde méthode, celle des restes, est pour vous : cliquez ici.
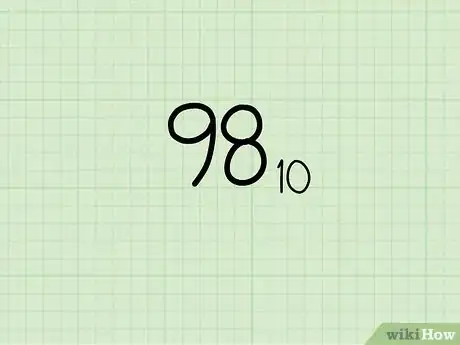
  2. Image intitulée Convert from Decimal to Octal Step 2
    2
    Inscrivez votre valeur en système décimal. Pour que les choses soient plus claires, nous nous donnons pour tâche de transformer 98 en base 8.
  3. Image intitulée Convert from Decimal to Octal Step 3
    3
    Inscrivez les puissances de 8. Le système de numération décimale utilise la base 10, ce qui signifie que chaque chiffre d’un nombre représente une puissance de 10. Ainsi, avec un nombre à trois chiffres, le chiffre de droite représente les unités (100 = 1), celui du milieu, les dizaines (101 = 10) et celui de gauche, les centaines (102 = 100). En base 8, le principe est le même, sauf qu’il faut prendre les puissances successives de 8. Sur votre feuille, inscrivez l’une sous l’autre les premières puissances de 8, avec leurs valeurs calculées.
    • 82  81  80
    • Inscrivez-les dans le même ordre, mais calculées :
    • 64  8  1
    • Il est inutile d’aller plus que le nombre que vous allez convertir en base 8. Nous avons choisi de convertir 98, vous pouvez vous arrêter à 82, car 83 = 512, lequel est supérieur à 98.
  4. Image intitulée Convert from Decimal to Octal Step 4
    4
    Divisez le nombre de départ par la plus grande puissance de 8. Dans le nombre 98, le 9 indique qu’il y a 9 dizaines. Ce chiffre de 9 a été obtenu en divisant 98 par 101, soit 10. En base 8, le principe est le même, il faut diviser le nombre à convertir par la plus forte puissance. C’est ainsi que 98 sera divisé par 64 et vous ne retiendrez que la partie entière du quotient. Les calculs en cascade se font horizontalement, de la gauche vers la droite [2] .
    • 98
      ÷
    • 64 (82)   8 (81)   1 (80)
      =
    • 1 ← ce sera le chiffre le plus à gauche de votre réponse.
  5. Image intitulée Convert from Decimal to Octal Step 5
    5
    Calculez le reste de cette première division. C’est le nombre qui reste de la division et qui est inférieur à au diviseur. Inscrivez ce reste sur la même ligne que le nombre de départ. Dans le cas choisi, vous avez divisé 98 par 64, il vous reste donc 34 (98 = (1 x 64) + 34). Inscrivez 34 en haut de la deuxième colonne.
    • 98   34
      ÷
    • 64   8   1
      =
    • 1
  6. Image intitulée Convert from Decimal to Octal Step 6
    6
    Divisez ce reste par la puissance de 8 inférieure. La procédure est la même que précédemment : vous divisez le reste par la puissance de 8 qui se trouve en dessous dans le tableau.
    • 98   34
      ÷     ÷
    • 64   8   1
      =    =
    • 1    4
  7. Image intitulée Convert from Decimal to Octal Step 7
    7
    Complétez entièrement le tableau. Vous mettrez au bas de la colonne, la partie entière du quotient trouvé et vous inscrirez le reste en haut de la colonne suivante. Quand vous n’avez plus de reste, la conversion est terminée : en haut à gauche, vous avez votre nombre en base 10 et la ligne de chiffres tout en bas est la réponse en base 8. Pour en revenir à notre exemple, divisez 34 par 8 : vous obtenez 4, le deuxième chiffre de votre nombre en base 8 et il vous reste 2 (34 = (4 x 8)+ 2). Dans la troisième colonne, vous divisez 2 par 80 (=1) et vous obtenez 2, sans reste.
    • 98   34   2
      ÷     ÷    ÷
    • 64   8   1
      =    =    =
    • 1    4    2
    • Votre réponse est : 98 en base 10 = 142 en base 8. Par convention, on écrit : 9810 = 1428.
  8. Image intitulée Convert from Decimal to Octal Step 8
    8
    Vérifiez vos calculs. Faites les calculs à l’envers, à savoir que vous allez multiplier chacun des chiffres de votre réponse par la puissance de 8 correspondante. Additionnez tous ces résultats et vous devriez retomber sur votre chiffre de départ. Dans notre exemple, vous opèrerez ainsi :
    • 2 x 80 = 2 x 1 = 2
    • 4 x 81 = 4 x 8 = 32
    • 1 x 82 = 1 x 64 = 64
    • faites la somme : 2 + 32 + 64 = 98, c’est bien le nombre de départ.
  9. Image intitulée Convert from Decimal to Octal Step 9
    9
    Essayez de réaliser cette conversion. Après la théorie, la pratique. Essayez de convertir en base 8, avec la méthode vue ici, le nombre 327. Utilisez la même disposition sur votre feuille et quand vous avez fini, comparez avec la solution ci-dessous, que vous ferez apparaitre en sélectionnant l’espace laissé en blanc.
    • Sélectionnez la zone ci-dessous pour voir la réponse (cliquez à gauche et allez vers la droite en maintenant le bouton enfoncé, comme pour sélectionner un texte visible qui est ici invisible) :
    • 327  7   7
      ÷     ÷    ÷
    • 64   8   1
      =    =    =
    • 5    0    7
    • La réponse est donc : 3278 = 5078.
    • (N’est-ce pas original de trouver un 0 en quotient ?)
    Publicité

Méthode 2
Méthode 2 sur 2:
Convertir en base 8 en gardant les restes

  1. Image intitulée Convert from Decimal to Octal Step 10
    1
    Partez d’un nombre en base 10. Nous prendrons comme exemple le nombre 670.
    • La méthode que nous allons voir est plus rapide que la précédente. Il est vrai aussi qu’il est plus difficile de comprendre comment elle opère, c’est pourquoi les débutants préfèrent la première.
  2. Image intitulée Convert from Decimal to Octal Step 11
    2
    Divisez votre nombre par 8. Ne gardez que la partie entière du quotient. Vous comprendrez mieux plus tard.
    • Dans notre exemple, 670 ÷ 8 = 83.
  3. Image intitulée Convert from Decimal to Octal Step 12
    3
    Trouvez le reste. Après avoir trouvé combien fois il allait 8 dans votre nombre, vous avez obligatoirement un reste qui par définition est strictement inférieur à 8 (sinon cela signifierait que vous vous êtes trompé dans la division) : il sera le dernier chiffre du nombre en base 8, l’unité en somme [3] .
    • Dans notre exemple, 670 ÷ 8 = 83 et il reste 6 ( 670 = (83 x8) + 6).
    • La réponse se présente ainsi : _ _ _ 6.
    • Si votre calculatrice est dotée de la fonction modulo (touche mod), celle qui calcule les restes, entrez « 670 mod 8 », puis validez.
  4. Image intitulée Convert from Decimal to Octal Step 13
    4
    Divisez le quotient précédent par 8. Après avoir posé le premier chiffre, revenez au quotient de la première division et divisez-le par 8. Comme précédemment, inscrivez la partie entière du quotient et calculez le reste. Celui-ci sera le deuxième chiffre du nombre en base 8, correspondant aux huitaines (81).
    • Dans notre exemple, nous avions trouvé que le quotient de 670 par 8 était 83.
    • 83 ÷ 8 = 10 et il reste 3.
    • La réponse se présente ainsi : _ _ 36.
  5. Image intitulée Convert from Decimal to Octal Step 14
    5
    Divisez à nouveau par 8. Revenez au quotient de la division précédente et divisez-le par 8. Inscrivez la partie entière du quotient et calculez le reste. Celui-ci sera le troisième chiffre du nombre en base 8, correspondant aux « soixante-quatraines » (82)… si le nom existait.
    • Dans l’exemple, nous avions trouvé que le quotient de 83 par 8 donnait un quotient de 10.
    • 10 ÷ 8 = 1 et il reste 2.
    • La réponse se présente ainsi : _ 236.
  6. Image intitulée Convert from Decimal to Octal Step 15
    6
    Divisez ainsi autant de fois que nécessaire. Il faudra continuer ainsi tant que vous n’obtiendrez pas un quotient égal à 0. Quand ce sera le cas, le dividende sera le premier chiffre du nombre en base 8. Vous en aurez terminé.
    • Dans notre exemple, le dernier quotient trouvé était 1.
    • 1 ÷ 8 = 0 et il reste 1.
    • Voilà ! La réponse est : 3708 = 1 2368. La base étant inférieure, le nombre d’arrivée est forcément plus grand que celui de départ.
  7. Image intitulée Convert from Decimal to Octal Step 16
    7
    Comprenez le principe de fonctionnement de cette méthode. À défaut de l’expliquer ici scientifiquement, il n’est pas interdit de prendre une image concrète [4] .
    • Imaginez une pile de 670 pièces de monnaie.
    • Faites des piles de huit pièces et mettez de côté les pièces restantes, dont le nombre est inférieur à 8. Ce reliquat de pièces sera le dernier chiffre de votre nombre en base 8.
    • Dans l’étape suivante, vous ferez des groupements de 8 piles de huit pièces, soit 64 pièces (82). Il vous restera un certain nombre de piles, forcément inférieur à 8 : ce nombre est le deuxième chiffre de votre nombre en base 8.
    • Continuez en faisant des groupements de 8 groupes de 8 groupes de 8 piles… vous devez comprendre la suite !
    Publicité

Résoudre quelques exercices de conversion

  • Convertissez en base 8 les nombres décimaux suivants. Utilisez la méthode que vous voulez, puis vérifiez vos réponses en sélectionnant, avec la souris (cliquez et maintenez comme pour sélectionner une zone visible), les espaces vides à droite des valeurs en base 10. Votre réponse sera présentée ainsi : xxx8.
  • 9910 = 1438
  • 36310 = 5538
  • 5 21010 = 121328
  • 47 56910 = 1347218

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ http://users.ece.utexas.edu/~valvano/embed/chap3/chap3.htm#OCTAL
  2. ↑ http://www.free-online-calculator-use.com/decimal-to-octal-converter.html
  3. ↑ http://mathforum.org/library/drmath/view/55738.html
  4. ↑ http://mathforum.org/library/drmath/view/55738.html

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 21 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 40 338 fois.
Catégories: Mathématiques
Publicité