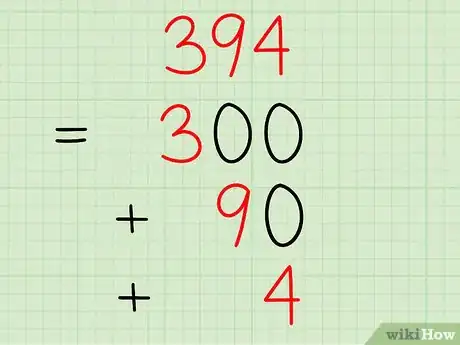X
wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, des auteur.e.s volontaires ont participé à l'édition et à l'amélioration.
Cet article a été consulté 15 208 fois.
Avec la décomposition des nombres, les jeunes élèves vont apprendre la structure de ces nombres et les liens qui existent entre les chiffres qui les composent. Ils apprendront également comment les nombres peuvent être manipulés dans certaines opérations. Il est possible de décomposer les nombres en centaines, dizaines et unités, comme il est possible de décomposer un nombre en sommes d'opérandes.
Étapes
Méthode 1
Méthode 1 sur 3:Décomposer un nombre en centaines, dizaines et unités [1]
Méthode 1
-
1Comprenez bien ce que sont les « dizaines » et les « unités ». Prenons un nombre entier (sans virgule) à deux chiffres. Ce nombre comporte des dizaines et des unités : les dizaines sont représentées par le chiffre de gauche, tandis que les unités le sont par celui de droite.
- Le chiffre des « unités » est un chiffre brut dans la mesure où il ne représente que lui-même. À l'emplacement des unités, on ne peut trouver qu'un chiffre entre 0 et 9 (zéro, un, deux, trois, quatre, cinq, six, sept, huit et neuf).
- Le chiffre des « dizaines » ressemble à n'importe quel chiffre des unités, mais en fait, il est sous-entendu que c'est un nombre composé de ce chiffre des dizaines, suivi d'un zéro. Les « dizaines » sont les suivantes : 10, 20, 30, 40, 50, 60, 70, 80 et 90 (dix, vingt, trente, quarante, cinquante, soixante, soixante-dix, quatre-vingts et quatre-vingt-dix).
-
2Décomposez un nombre à deux chiffres. Un tel nombre est donc composé d'un chiffre des « unités » et d'un chiffre des « dizaines ». Pour le décomposer, il faut séparer les dizaines des unités, en deux parties donc !
-
Exemple : décomposez le nombre 82.
- Le 8 représente les « dizaines », donc on peut le séparer et l'écrire sous la forme : 80.
- Le 2 représente les « unités », il reste sous la forme : 2.
- Votre réponse sera au final : 82 = 80 + 2.
- Un nombre écrit « normalement » (avec des chiffres) est dit écrit sous sa « forme numérique », mais quand il est décomposé comme on l'a vu, on parle alors de « forme étendue » ou de « décomposition additive ».
- Ainsi écrit, 82 apparait sous sa forme numérique. Quand on l'écrit sous la forme 80 + 2, on parle de « forme étendue » ou de « décomposition additive ».
-
Exemple : décomposez le nombre 82.
-
3Où se trouvent les « centaines » ? Prenons un nombre entier (sans virgule) à trois chiffres. Ce nombre comporte des centaines, des dizaines et des unités : les centaines sont représentées par le chiffre de gauche, les dizaines, par celui du milieu et les unités, par celui de droite.
- Les emplacements des unités et des dizaines sont exactement les mêmes que pour les nombres à deux chiffres.
- Le chiffre des « centaines » ressemble à n'importe quel chiffre des unités, mais en fait, il est sous-entendu que c'est un nombre composé de ce chiffre des centaines, suivi de deux zéros. Les centaines sont les suivantes : 100, 200, 300, 400, 500, 600, 700, 800 et 900 (cent, deux-cents, trois-cents, quatre-cents, cinq-cents, six-cents, sept-cents, huit-cents et neuf-cents).
-
4Décomposez un nombre à trois chiffres. Un tel nombre est donc composé d'un chiffre des « unités », d'un chiffre des « dizaines » et d'un chiffre des « centaines ». Pour le décomposer, il faut séparer les centaines des dizaines et des unités, en trois parties donc !
-
Exemple : décomposez le nombre 394.
- Le 3 représente les « centaines », donc on peut le séparer et l'écrire sous la forme : 300.
- Le 9 représente les « dizaines », donc on peut le séparer et l'écrire sous la forme : 90.
- Le 4 représente les « unités », il reste sous la forme : 4.
- La décomposition se présente ainsi : 394 = 300 + 90 + 4.
- Ainsi écrit, le nombre 394 apparait sous sa forme numérique. Quand on l'écrit sous la forme 300 + 90 + 4, on parle de « forme étendue » ou de « décomposition additive ».
-
Exemple : décomposez le nombre 394.
-
5Appliquez cette méthode aux grands nombres. En effet, on peut utiliser le même procédé pour décomposer de grands (voire de très grands !) nombres.
- Dans un nombre, tous les chiffres le composant peuvent être remplacés par leurs vraies valeurs. Si on décompose le nombre, on pourra alors remplacer ce chiffre par un nombre composé de ce chiffre et d'autant de zéros qu'il y a de chiffres sur sa droite. Cela marche toujours et pour tous les nombres, si grands soient-ils !
- Exemple : 5 394 128 = 5 000 000 + 300 000 + 90 000 + 4 000 + 100 + 20 + 8.
-
6Comprenez comment sont structurés les nombres décimaux. Il est également possible de décomposer les nombres décimaux, mais tous les chiffres placés après (à droite de) la virgule doivent être décomposés en autant de chiffres décimaux, avec une virgule donc.
- Le chiffre des « dixièmes » se situe au premier rang après (à droite de) la virgule.
- Le chiffre des « centièmes » se situe à deux rangs après la virgule.
- Le chiffre des« millièmes » se situe à trois rangs après la virgule.
-
7Décomposez un nombre décimal. Avec ce genre de nombres, vous avez des chiffres à droite et à gauche de la virgule. Lors de la décomposition, il faut s'en occuper séparément.
- Pour ce qui est de la partie à gauche de la virgule (appelée « partie entière »), on décompose comme on l'a vu précédemment : c'est un entier comme un autre. Faites comme s'il n'y avait rien après la virgule.
-
Exemple : décomposez le nombre 431,58.
- Le 4 représente les « centaines », donc on peut le séparer et l'écrire sous la forme : 400.
- Le 3 représente les « dizaines », donc on peut le séparer et l'écrire sous la forme : 30.
- Le 1 représente les « unités », il reste sous la forme : 1.
- Le 5 représente les « dixièmes », donc on peut le séparer et l'écrire sous la forme : 0,5.
- Le 8 représente les « centièmes », donc on peut le séparer et l'écrire sous la forme : 0,08.
- La décomposition finale se présente ainsi : 431,58 = 400 + 30 + 1 + 0,5 + 0,08.
Publicité
Méthode 2
Méthode 2 sur 3:Décomposer un nombre en opérandes [2]
[3]
Méthode 2
-
1Comprenez bien de quoi il retourne. La décomposition d'un nombre en opérandes (des chiffres ou des nombres, en fait !) consiste à trouver toutes les additions à deux nombres (ou chiffres) qui donnent votre nombre de départ.
- Si vous prenez un opérande et que vous le soustrayez du nombre de départ, vous obtenez le deuxième opérande.
- Quand vous additionnez ensuite ces deux opérandes, vous retrouvez votre nombre de départ.
-
2Commencez par un chiffre. Un chiffre est un… « nombre » qui n'a que des unités ! On va prendre un chiffre, car la démonstration est plus simple.
- Pour décomposer un grand nombre, vous pouvez bien sûr réutiliser les principes vus dans la partie ci-dessus, intitulée « Décomposer un nombre en centaines, dizaines et unités ». Cependant, dans ce cas-là, les combinaisons d'opérandes sont tellement nombreuses que cette méthode est impossible à mettre en œuvre, sauf dans certains cas.
-
3Trouvez toutes les combinaisons d'opérandes qui donnent votre nombre (chiffre). Pour décomposer un nombre en ses sommes d'opérandes, il faut inscrire toutes les combinaisons de chiffres et de nombres qui donnent votre nombre de départ. Les opérandes sont toujours plus petits que le nombre de références.
-
Exemple : décomposez le nombre 7 en sommes de deux opérandes.
- 7 = 0 + 7
- 7 = 1 + 6
- 7 = 2 + 5
- 7 = 3 + 4
- 7 = 4 + 3
- 7 = 5 + 2
- 7 = 6 + 1
- 7 = 7 + 0
-
Exemple : décomposez le nombre 7 en sommes de deux opérandes.
-
4Utilisez des objets concrets pour vous aider. Pour les débutants, il est peut-être bon de voir réellement comment fonctionne cette décomposition. Rien ne vaut le concret !
- Réunissez un certain nombre d'objets. Ainsi, si vous voulez comprendre le nombre 7, vous pouvez mettre 7 dragées gélifiées sur votre table.
- Séparez-les en deux tas, l'un à gauche, composé d'une seule dragée, l'autre à droite, composé du reste. Comptez les dragées du second tas. Vos sept dragées ont été décomposées en un tas « d'une seule » dragée et un tas de « six » dragées.
- Continuez à faire deux tas en déplaçant successivement une dragée depuis le tas de droite vers celui de gauche. Comptez à chaque fois le nombre de dragées de chaque tas.
- On a pris ici des dragées, mais vous auriez aussi bien pu prendre des bonbons, de petits carrés de papier, des épingles à linge, des cubes, des boutons…
Publicité - Réunissez un certain nombre d'objets. Ainsi, si vous voulez comprendre le nombre 7, vous pouvez mettre 7 dragées gélifiées sur votre table.
Méthode 3
Méthode 3 sur 3:Décomposer des nombres pour faire des opérations [4]
Méthode 3
-
1Prenons l'exemple d'une petite addition. Vous pouvez vous servir des deux types de décompositions vues précédemment pour faire la somme.
- Cette méthode est pratique pour les petites additions. Elle l'est beaucoup moins pour des additions à multiples opérandes.
-
2Décomposez chacun des nombres constituant l'opération. Prenez chacun des nombres et décomposez-les en dizaines et en unités. Si cela s'avère nécessaire, rien ne vous empêche de décomposer à nouveau les unités.
-
Exemple : décomposez, puis faites l'opération suivante : 31 + 84
- 31 peut être décomposé sous la forme : 30 + 1
- 84 peut être décomposé sous la forme : 80 + 4
-
Exemple : décomposez, puis faites l'opération suivante : 31 + 84
-
3Récrivez l'opération pour qu'elle soit plus facile à faire. L'opération peut être récrite sans modification, c'est-à-dire dans l'ordre de la décomposition ou bien réorganisée pour mettre ensemble les chiffres « ronds », comme les centaines, les dizaines… Cette dernière façon de faire facilite l'addition.
- Exemple : 31 + 84 = 30 + 1 + 80 + 4 = 30 + 80 + 1 + 4 = 30 + 80 + 5 = 100 + 10 + 5
-
4Faites l'opération. Après avoir récrit l'opération de la façon qui vous parait la plus logique ou pratique, il vous suffit de tout additionner.
- Exemple : 100 + 10 + 5 = 115
Publicité
Références
À propos de ce wikiHow
Publicité