Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 7 278 fois.
Toute fonction mathématique () contient deux types de variables : les variables indépendantes et les variables dépendantes, les secondes… dépendant des premières. Dans la fonction , est la variable indépendante et la dépendante. Partant, le domaine de définition () est l'ensemble des valeurs de pour lesquelles un existe. Quant à l'ensemble image, , c'est l'ensemble des valeurs de pour tous les du domaine de définition [1] .
Étapes
Partie 1
Partie 1 sur 3:Trouver le domaine de définition d'une fonction
-
1Déterminez le type de votre fonction. Le domaine de définition d'une fonction regroupe toutes les valeurs de pour lesquelles un existe. Il existe de très nombreuses fonctions (affines, second degré, exponentielles…) qui chacune ont des domaines de définition particuliers. Pour déterminer le type de votre fonction, vous devez regarder la forme de votre équation.
- Une fonction du second degré se présente sous la forme [2] , comme .
- Il existe aussi des fonctions rationnelles composées d'un rapport, comme les fonctions et .
- Est une fonction racine toute fonction comprenant une racine, comme
, ou .
-
2Présentez correctement le domaine de définition. Un domaine de définition est noté avec des valeurs limites encadrées de crochets inclusifs ([2… ou …4], le 2 et le 4 sont dans le domaine de définition) ou exclusifs (…2[, ]4…, le 2 et le 4 ne sont pas dans le domaine de définition). Le lettre est en fait le symbole de l'union, elle est utilisée dans le cas où une fonction est définie sur deux intervalles séparés [3] .
- Ainsi, si vous avez une fonction ayant pour domaine de définition l'union des intervalles , peut prendre n'importe quelle valeur entre -2 et 12 (toutes deux incluses), sauf qui n'est pas dans le domaine de définition.
- Si votre ensemble a une borne en (plus l'infini) et (moins l'infini), les crochets sont toujours exclusifs ( et ) : en fait, l'infini n'est pas une valeur, mais un concept… illimité, d'où l'exclusion.
-
3Tracez le graphe d'une fonction du second degré. Une telle fonction a comme graphe une parabole, ouverte vers le bas ou vers le haut. Chaque fois que vous entrez une valeur de , la parabole tend de plus en plus vers l’infini, aussi peut-il prendre n'importe quelle valeur. Une fonction polynôme du second degré est définie sur la totalité de l'ensemble des nombres réels ( [4] ).
- Pour commencer, prenez pour n'importe quelle valeur (0, 1, -1…), puis calculez f(x). En combinant et son image (aussi dénommée ), vous obtenez un premier point de la parabole dont les coordonnées sont (,).
- Placez ce premier point et recommencez avec une autre abscisse.
- Au bout de quelques points, surtout si vous choisissez des abscisses opposées (1 et -1, 4 et -4…), vous allez très vite voir la forme générale de la courbe.
-
4Trouvez la valeur de qui annule un dénominateur. Si l'équation d'une fonction est une fraction, vous devez être vigilant(e), car un dénominateur ne doit jamais être nul, car la division par 0 est impossible. Pour trouver cette valeur, vous devez poser le dénominateur égal à 0 et trouvez [5] .
- Pour éclairer le propos, prenons la fonction rationnelle suivante : et déterminons son ensemble définition.
- Le dénominateur de cette fonction est donc .
- Posez le dénominateur égal à 0 et trouvez : , donc .
- Présentez le domaine de définition. peut prendre n'importe quelle valeur entre et , sauf la valeur 1. En conséquence, son domaine de définition est :
. - Cette écriture [ est bien compliquée pour simplement exprimer le fait que peut prendre n'importe quelle valeur de , sauf 1. Si cet exemple est caricatural, pour d'autres fonctions, le domaine de définition est l'union de plusieurs intervalles plus complexes.
-
5Trouvez les valeurs qui donnent un radicande positif. Cette opération doit être faite dans le cas où l'inconnue est en radicande. Par définition, il n'est pas possible de calculer la racine d'une valeur négative. Toute valeur de qui ne respecte pas cette obligation est exclue du domaine de définition [6] .
- Déterminons le domaine de définition de : .
- Le radicande est donc .
- Ce radicande doit être obligatoirement positif : .
- Définissez : .
- Le domaine de définition de cette fonction est constitué de tous les nombres supérieurs ou égaux à - 3, ce qui s'écrit : .
Publicité
Partie 2
Partie 2 sur 3:Déterminer l'ensemble image d'une fonction du second degré
-
1Vérifiez que vous avez bien une fonction du second degré. Une telle fonction se présente sous la forme (par exemple,
. Une fonction du second degré est graphiquement représentée par une parabole ouverte vers le haut ou le bas. L'ensemble image d'une telle fonction peut se faire par le calcul ou graphiquement [7] .- L'ensemble image des fonctions (second degré, rationnelles…) peut se déterminer graphiquement sur une calculatrice ou sur du papier, mais aussi par le calcul.
-
2Déterminez l'abscisse du sommet de la fonction. Le sommet est ce point de la courbe à partir duquel s'opère un changement de direction. L'abscisse de ce sommet a pour formule : si l'équation est sous la forme . Le sommet est le point où la dérivée de la fonction s'annule, et c'est en . La pente à l'approche du sommet devient nulle [8] .
- Admettons que vous deviez définir l'ensemble image de la fonction
. - Calculez l'abscisse du sommet : .
- Admettons que vous deviez définir l'ensemble image de la fonction
-
3Déterminez l'ordonnée du sommet de la fonction. Dans l'équation de la fonction, remplacez par l'abscisse du sommet et vous obtenez l'ordonnée de ce sommet. Cette ordonnée est une borne de l'ensemble image.
- Calculez l'ordonnée :
- Le sommet a pour coordonnées (-1, -5).
-
4Déterminez la direction de la parabole. Prenez une autre abscisse () et calculez son image (). Marquez sur votre repère ce point : s'il est au-dessus du sommet, alors la parabole est ouverte vers le haut et l'autre borne de l'ensemble image est . S'il est au-dessous, la parabole s'ouvre vers le bas et l'autre borne de l'ensemble image est .
- Trouvez l'image () de l'abscisse -2 :
- Vous avez un point de coordonnée (-2, -2).
- Ce point se trouve au-dessus du sommet : l'ensemble image est composé de toutes les valeurs de supérieures à -5.
- L'ensemble image de cette fonction est : .
- Trouvez l'image () de l'abscisse -2 :
-
5Présentez l'ensemble image selon les normes en vigueur. La notation de l'ensemble image suit exactement les mêmes règles de présentation que celle du domaine de définition, à savoir des crochets inclusifs ou exclusifs, des virgules et le symbole (union) en cas d'intervalles distants [9] .
- L'ensemble image signifie que peut prendre n'importe quelle valeur de ces intervalles, 2 et 12 incluses, à l'exception de
- Pour une borne en et , les crochets sont toujours exclusifs (] et [).
Publicité
Partie 3
Partie 3 sur 3:Trouver graphiquement l'ensemble image d'une fonction
-
1Tracez le graphe de la fonction. L'ensemble image d'une fonction du second degré, dont le graphe est une parabole, est du type ou , étant l'ordonnée du sommet. Celui d'une fonction rationnelle est du type ou , étant la valeur d'annulation du dénominateur ( est l'équation de l'asymptote). Quant à celui d'une fonction racine, son ensemble image est du type , étant la constante de la fonction [10] .
- Les paraboles n'ont pas toutes leurs sommets sur l'axe des abscisses. Quoi qu'il en soit, l'ensemble image est toujours déterminé par l'ordonnée de ce sommet. Si une parabole a son sommet en et s'ouvre vers le haut, son ensemble image est .
- Il est bien pratique de recourir à un traceur de courbes ou une calculatrice graphique pour avoir rapidement le graphe.
- Si vous n'avez pas de calculatrice graphique, faites votre repère sur une feuille, tracez la courbe en plaçant quelques points. Si deux ou trois points ne suffisent pas, ajoutez-en d'autres jusqu'à deviner la forme générale de la courbe.
-
2Déterminez le minimum de la fonction. Votre graphe est tracé et normalement, vous devriez voir clairement quel est le point le plus bas du graphe. Si ce n'est pas le cas, alors c'est que la fonction tend vers .
- L'ensemble image d'une fonction rationnelle est souvent auquel on a retiré la racine () du polynôme en dénominateur et se présente sous la forme
.
- L'ensemble image d'une fonction rationnelle est souvent auquel on a retiré la racine () du polynôme en dénominateur et se présente sous la forme
-
3Déterminez le maximum de la fonction. Votre graphe est tracé et normalement, vous devriez voir clairement quel est le point le plus haut du graphe. Si ce n'est pas le cas, alors c'est que la fonction tend vers .
-
4Présentez l'ensemble image selon les normes en vigueur. La notation de l'ensemble image suit exactement les mêmes règles de présentation que celle du domaine de définition, des crochets inclusifs ou exclusifs, des virgules et le symbole (union) en cas d'intervalles distants [11] .
- L'ensemble image signifie que peut prendre n'importe quelle valeur de ces intervalles, 2 et 12 incluses, à l'exception de .
- Pour les bornes en et , les crochets sont toujours exclusifs (] et [).
Publicité
Références
- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U17_L2_T3_text_final.html
- ↑ http://hotmath.com/hotmath_help/topics/quadratic-function.html
- ↑ http://www.biology.arizona.edu/biomath/tutorials/notation/setbuildernotation.html
- ↑ http://hotmath.com/hotmath_help/topics/quadratic-function.html
- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U17_L2_T3_text_final.html
- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U17_L2_T3_text_final.html
- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U17_L2_T3_text_final.html
- ↑ http://hotmath.com/hotmath_help/topics/quadratic-function.html
- ↑ http://www.biology.arizona.edu/biomath/tutorials/notation/setbuildernotation.html
















![{\displaystyle [-2,10[\ \cup \ ]10,12]}](./images/1730289504-40f9e4588306c86accc9145927b8ade0626dd867.webp)



![{\displaystyle ]-\infty }](./images/1982144558-a8e693cb28c9ec7695c8950cf06c285d7f9f4eae.webp)



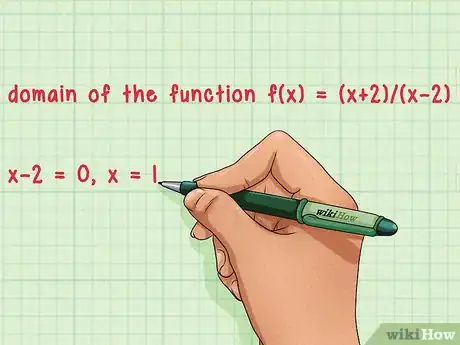



![{\displaystyle D_{f}=]-\infty ,1[\ \cup \ ]1,+\infty [}](./images/1902976899-2df141ad4e8e89790fce379f910033c17c0d65b8.webp)
![{\displaystyle ]-\infty ,1[\ \cup \ ]1,+\infty }](./images/1933844564-48d178adf01233c6d5ff56d20adaf0f131aba7bf.webp)











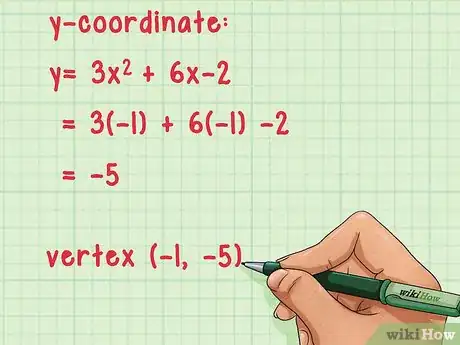






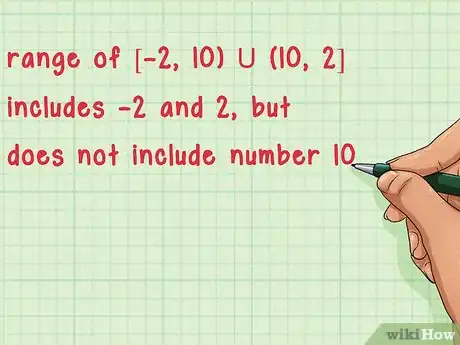

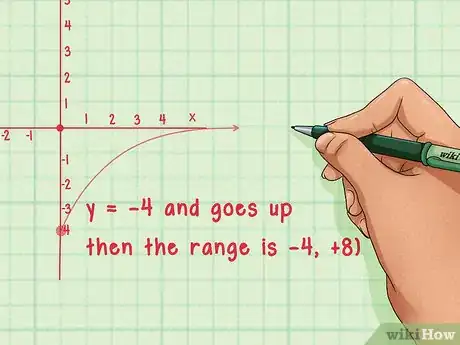
![{\displaystyle ]-\infty ,s]}](./images/1984700409-4f86464afdd6a827e78e3fe5570e8fff55c044e4.webp)


![{\displaystyle ]-\infty ,r[}](./images/1777344282-8e318ed0ab9743cf61e414550547cd3704a355d8.webp)
![{\displaystyle ]r,+\infty [}](./images/2032869443-81631cfe19ce6d3ca6e73b688fab4ed4b8605d6b.webp)







![{\displaystyle ]-\infty ,r[\ \cup \ ]r,+\infty [}](./images/1720459091-87b0335b98f3121b98ebffe1176f327f07723bc6.webp)





















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 7 278 fois.