Comment déterminer l'équation d'une droite perpendiculaire à une autre

Il est assez facile de trouver l'équation d'une droite perpendiculaire (intersection à angle droit) à une autre. Il faut cependant des conditions, comme avoir l'équation de la première droite et les coordonnées d'un point de la perpendiculaire. Cela est également possible avec les coordonnées de 3 points, deux servant à tracer une droite et le troisième étant sur la perpendiculaire à cette droite. Nous évoquerons le cas de droites affines d'équations $y=ax+b$ . Les coordonnées $x$ et $y$ sont celles d'un quelconque point de la droite, $a$ en est le coefficient directeur et $b$ l'ordonnée à l'origine (quand $x=0$ ^{[1]
X
Source de recherche}).

Méthode 1

Méthode 1 sur 2:
À partir d'un point et d'une équation

1
Arrangez l'équation de la droite de départ. Vous avez un exercice dans lequel vous avez une fonction affine et un point. Le travail consiste à trouver l'équation de la droite perpendiculaire à celle de la fonction affine et passant par le point donné. Pour bien démarrer, l'équation de la droite de référence doit se présenter sous la forme $y=ax+b$ $y=ax+b$ . Si elle est déjà sous cette forme, c'est parfait, sinon il faut isoler $y$ $y$ à gauche ^{[2]
X
Source de recherche}.
- À titre d'exemple, nous allons travailler sur la droite d'équation $5y-x=10$ .
- Pour isoler $y$ , vous devez d'abord faire passer $-x$ dans l'autre membre en ajoutant $x$ des deux côtés, ce qui donne : $5y=x+10$ .
- Pour ne garder que ${y}$ dans le membre de gauche, il faut diviser les deux membres de l'équation par $5$ , lequel est le coefficient du monôme $5y$ .
- L'équation se présente alors ainsi : $y={\frac {x}{5}}+{\frac {10}{5}}$ ou, une fois simplifiée,
  $y={\frac {x}{5}}+2$ qui est la même chose que $y={\frac {1}{5}}x+2$ .
2
Calculez l'opposée inverse de la pente. Toute droite perpendiculaire à une autre a comme comme pente (ou coefficient directeur) l'opposée inverse de celle de l'autre droite. Les deux droites se croisant à angle droit, les pentes ont des signes opposés. Le produit des coefficients directeurs de deux droites perpendiculaires est toujours égal à $-1$ $-1$ ^{[3]
X
Source de recherche}.
- Pour rappel, dans une équation du type $y=ax+b$ , $a$ est ce que l'on appelle le coefficient directeur de la droite, soit sa pente.
- Dans l'équation $y={\frac {1}{5}}x+2$ , la pente est ${\frac {1}{5}}$ et son opposée inverse est ${-}{\frac {5}{1}}$ , soit $-5$ .
3
Déterminez l'ordonnée à l'origine de la perpendiculaire. Vous avez sa pente, $a$ $a$ , il faut trouver l'ordonnée à l'origine, $b$ $b$ , en vous servant de l'équation
$y=ax+b$ $y=ax+b$ . Remplacez $x$ $x$ et $y$ $y$ par les coordonnées du point de la perpendiculaire, faites les calculs permettant de calculer $b$ $b$ ^{[4]
X
Source de recherche}.
- Pour rappel, $b$ est ce que l'on appelle l'ordonnée à l'origine, l'ordonnée quand
  $x=0$ .
- Reprenons l'exemple d'une droite perpendiculaire à celle d'équation
  $y={\frac {1}{5}}x+2$ et passant par le point ${\begin{pmatrix}8\\2\end{pmatrix}}$ (abscisse $x=8$ et ordonnée
  $y=2$ ).
- Dans l'ébauche d'équation de la perpendiculaire $y=-5x+b$ , faites l'application numérique avec les coordonnées du point et la pente (opposée inverse), ce qui donne l'équation suivante : $2={-5}(8)+b$ , soit
  $2=-40+b$ .
4
Calculez l'ordonnée à l'origine $b$ . C'est ainsi que l'on appelle l'ordonnée du point qui est à l'intersection de l'axe des y et du graphe de la fonction. Avec les fonctions affines, son calcul est toujours simple, il faut juste faire attention aux signes lors des passages d'un membre de l'équation à l'autre. Après calcul des valeurs numériques, isolez $b$ $b$ dans le membre de gauche ^{[5]
X
Source de recherche}.
- Pour isoler $b$ , ajoutez ${40}$ des 2 côtés : $(40)+2=(40)-40+b$ , soit
  $b=42$ .
- Résultat : pour $x=0$ , $y=42$ , c'est l'ordonnée à l'origine de la droite perpendiculaire.
5
Établissez l'équation de la droite perpendiculaire. Vous avez calculé la pente, puis l'ordonnée à l'origine, le travail est quasiment fini, il suffit d'écrire correctement l'équation sous la forme $y=ax+b$ $y=ax+b$ . $x$ $x$ et $y$ $y$ restent tels quels, $a$ $a$ est remplacé par la pente et $b$ $b$ par l'ordonnée à l'origine ^{[6]
X
Source de recherche}.
- L'équation de la droite perpendiculaire est donc la suivante : $y={-5}x+42$ .
Publicité

Méthode 2

Méthode 2 sur 2:
À partir de trois points

1
Comprenez bien cet exercice avec trois points. Une droite ne peut passer que par 2 points et donc le troisième point ne peut être, dans ce contexte-là, qu'un point sur la perpendiculaire à la première droite, ce qui fait que vous retombez un peu sur la méthode précédente à la différence près que vous n'avez pas l'équation de la droite de départ. Donc, vous allez établir l'équation de la droite passant par 2 points, puis celle, perpendiculaire, passant par le dernier point, toutes deux seront sous la forme $y=ax+b$ $y=ax+b$ ^{[7]
X
Source de recherche}.
- Exercice : vous avez à trouver l'équation d'une droite passant par le point de coordonnées $(6,1)$ , perpendiculaire à une droite supposée passer par les points de coordonnées $(4,6)$ et $(2,3)$ .
- Concentrez-vous en priorité sur les deux points $(4,6)$ et $(2,3)$ , lesquels déterminent la droite de référence.
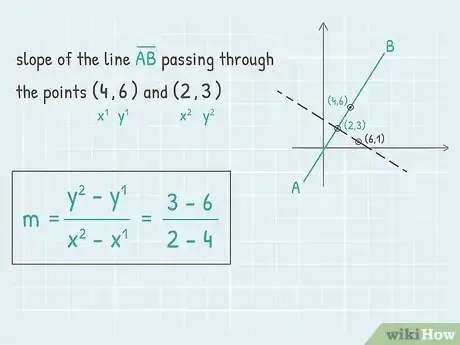
2
Déterminez la pente $a$ de la première droite. Peu importe les deux points sur les trois que vous prenez, sauf s'il vous est clairement indiqué lesquels prendre. Cette pente est assez facile à calculer grâce à une formule toute prête à partir des seules coordonnées des 2 points. Pour une droite passant par les points $A\ {\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}$ $A\ {\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}$ et $B\ {\begin{pmatrix}x_{2}\\y_{2}\end{pmatrix}}$ $B\ {\begin{pmatrix}x_{2}\\y_{2}\end{pmatrix}}$ , la pente est la suivante : $a={\frac {{y_{2}}-{y_{1}}}{{x_{2}}-{x_{1}}}}$ $a={\frac {{y_{2}}-{y_{1}}}{{x_{2}}-{x_{1}}}}$ . Faites très attention à l'ordre des coordonnées, sans quoi votre résultat sera faux ^{[8]
X
Source de recherche} !
- À partir de vos deux points $(4,6)$ et $(2,3)$ , vous pouvez en conclure que la pente de la droite qui passe par ces 2 points est : $a={\frac {3-6}{2-4}}$ .
- Calculez $a={\frac {3-6}{2-4}}$ . L'opération est simple et donne donc une pente de ${\frac {-3}{-2}}$ que l'on peut encore simplifier en ${\frac {3}{2}}$ .
- La pente (ou coefficient directeur) de la droite de référence est donc : ${\frac {3}{2}}$
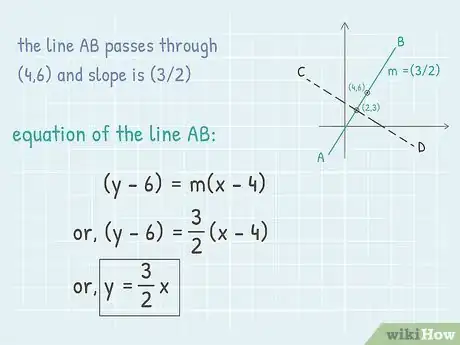
3
Déterminez l'équation de la première droite. La pente étant désormais connue, il ne reste plus qu'à établir l'équation de la droite passant ces 2 mêmes points. L'équation est de la forme grâce à la formule :
${y_{2}}-{y_{1}}=a({x_{2}}-{x_{1}})$ ${y_{2}}-{y_{1}}=a({x_{2}}-{x_{1}})$ . Pour voir sa forme théorique, il faut remplacer dans cette équation de base une des paires de coordonnées et d'anonymer l'autre ^{[9]
X
Source de recherche}.
- Prenons le point $B\ {\begin{pmatrix}4\\6\end{pmatrix}}$ situé sur la droite de référence. L'équation s'établit comme suit : ${y}-{6}={\frac {3}{2}}({x}-{4})$ .
4
Mettez en forme l'équation de la droite. Le travail est quasiment terminé. L'équation doit de préférence se présenter sous la forme $y=ax+b$ $y=ax+b$ . Il est rare que l'équation se présente immédiatement sous cette forme sans petits calculs. Faites les opérations, puis isolez $y$ $y$ à gauche ^{[10]
X
Source de recherche}.
- L'équation brute était donc ${y}-6={\frac {3}{2}}(x-4)$ . Développez, puis simplifiez le produit de droite : ${y}-6={\frac {3}{2}}{x}-{\frac {12}{2}}$ , soit ${y}-6={\frac {3}{2}}{x}-6$ .
- Isolez $y$ à gauche en ajoutant $6$ de chaque côté de l'équation, ce qui donne le résultat suivant : ${y}={\frac {3}{2}}{x}$ , soit l'équation de la droite de référence.
5
Déterminez la pente de la droite perpendiculaire. Il suffit d'inverser la pente $a$ $a$ de la droite de départ et lui donner le signe opposé : c'est l'opposée inverse
( ${\frac {-1}{a}}$ ${\frac {-1}{a}}$ ). Si la pente de la droite de référence est un entier positif, celle d'une droite qui lui est perpendiculaire sera un nombre rationnel négatif, une fraction pour faire simple. Le produit des coefficients directeurs de deux droites perpendiculaires est toujours égal à $-1$ $-1$ ^{[11]
X
Source de recherche}.
- L'opposée inverse de ${\frac {3}{2}}$ est ${-}{\frac {2}{3}}$ .
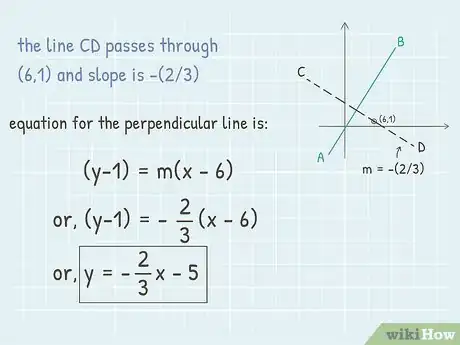
6
Établissez l'équation de la droite perpendiculaire. Vous venez de calculer la pente, il ne vous reste plus qu'à utiliser les coordonnées du point situé sur cette droite pour établir l'équation de cette perpendiculaire. Donc, l'équation se présentera sous la forme $y={-}{\frac {2}{3}}x+b$ $y={-}{\frac {2}{3}}x+b$ , $b$ $b$ étant l'ordonnée à l'origine. Comme dans la méthode précédente, vous allez utiliser la formule d'équation ${y^{2}}-{y^{1}}=a({x^{2}}-{x^{1}})$ ${y^{2}}-{y^{1}}=a({x^{2}}-{x^{1}})$ , $a$ $a$ sera remplacé par sa valeur trouvée ^{[12]
X
Source de recherche}.
- Le troisième point $B\ {\begin{pmatrix}6\\1\end{pmatrix}}$ est donc sur la droite perpendiculaire. L'équation s'établit comme suit : ${y}-{1}=-{\frac {2}{3}}({x}-{6})$ .
- Après calcul du produit de droite, l'équation est la suivante :
  ${y}-{1}=-{\frac {2}{3}}{x}-(-{\frac {12}{3}})$ , soit ${y}-{1}=-{\frac {2}{3}}{x}+4$
- Isolez $y$ en ajoutant $1$ aux 2 membres de l'équation :
  ${y}-1+{\mathit {1}}=-{\frac {2}{3}}{x}+4+{\mathit {1}}$ , soit $y={-}{\frac {2}{3}}x+5$ .
- L'équation se présente ainsi : $y={-}{\frac {2}{3}}x+5$ . C'est l'équation que vous recherchiez, celle de la droite perpendiculaire.
Publicité