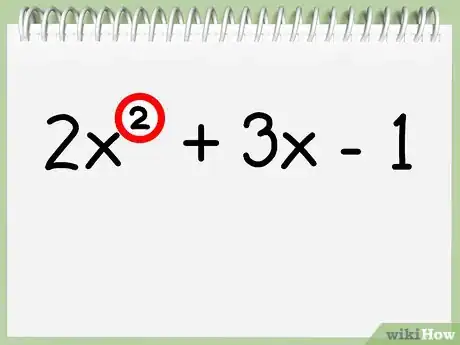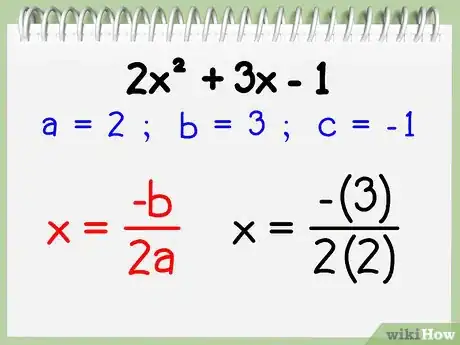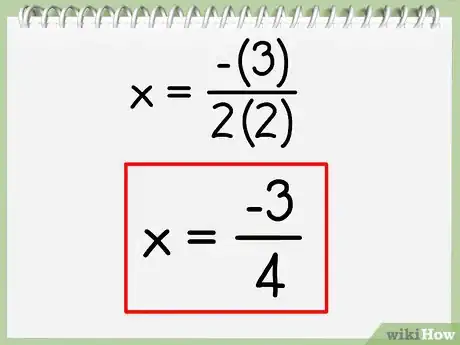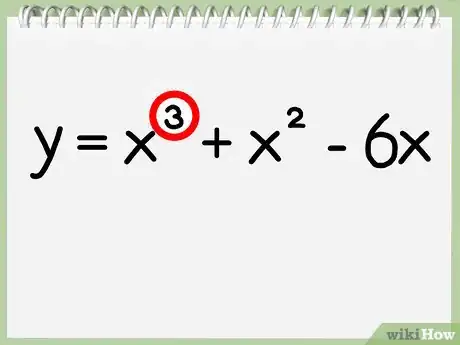Comment déterminer un axe de symétrie

Informations concernant l'auteur.e

La courbe d'un polynôme ou d'une fonction révèle de nombreuses caractéristiques qui peuvent être difficiles à déterminer sans une représentation visuelle. L'axe de symétrie fait partie de l'une de ces caractéristiques : c'est une ligne verticale sur un graphe qui divise ce dernier en deux images symétriques. Trouver l'axe de symétrie d'un polynôme donné est quelque chose de très simple et, pour ce faire, il y a deux méthodes basiques, que nous vous invitons à découvrir ici.

Méthode 1

Méthode 1 sur 2:
Déterminer l'axe de symétrie d'une fonction polynôme du second degré

1
Vérifiez le degré de votre polynôme. Le degré (ou l'ordre) d'un polynôme est simplement représenté par le plus grand exposant de l'expression. Si votre polynôme est du second degré (c'est-à-dire qu'il n'y a aucun exposant supérieur à x²), vous pouvez déterminer l'axe de symétrie en utilisant cette méthode. Si par contre le degré du polynôme est supérieur à 2, utilisez la méthode 2.
- À titre illustratif, prenons par exemple le polynôme 2x² + 3x – 1. L'exposant le plus élevé ici est x², ce qui veut dire qu'il s'agit d'un polynôme d'ordre 2 et vous pouvez utiliser cette première méthode pour déterminer l'axe de symétrie.
2
Insérez vos variables dans la formule de l'axe de symétrie. Pour calculer l'axe de symétrie d'un polynôme d'ordre 2 sous la forme ax² + bx +c (une parabole), il est recommandé d'utiliser la formule de base que voici : x = -b / 2a.
- Dans l'exemple ci-dessus, a = 2, b = 3 et c = -1. Entrez ces valeurs dans la formule et vous obtiendrez :
  x = -3 / 2(2) = -3/4.
3
Écrivez l'équation de l'axe de symétrie. La valeur que vous obtenez à partir de la formule de l'axe de symétrie est la coordonnée x du point d'intersection de cet axe de symétrie.
- Dans l'exemple ci-dessus, la valeur de l'axe de symétrie est -3/4.
Publicité

Méthode 2

Méthode 2 sur 2:
Déterminer graphiquement l'axe de symétrie

1
Vérifiez le degré de votre polynôme. Le degré (ou l'ordre) d'un polynôme est simplement représenté par la valeur du plus grand exposant de l'expression. Si votre polynôme est de degré 2 (c'est-à-dire que x² est l'exposant le plus grand), vous pouvez déterminer l'axe de symétrie en utilisant la formule énoncée ci-dessus. Si le degré du polynôme est supérieur à 2, utilisez alors cette méthode graphique.
2
Représentez les axes x et y. Représentez deux droites sous la forme d'un signe plus. La droite horizontale représente l'axe des x et celle verticale l'axe des y.
3
Graduez votre graphisme. Graduez les deux axes avec des chiffres à des intervalles égaux. L'espacement doit être uniforme sur les deux axes.
4
Déterminez y = f(x) pour chaque x. Observez bien l'expression de votre polynôme ou de votre fonction et calculez les valeurs de f(x) en y intégrant toutes les valeurs de x.
5
Marquez les points pour chaque paire du graphique. Vous avez à présent les paires de y = f(x) pour chaque x sur l'axe. Pour chaque paire (x, y), faites un point sur le graphe, c'est-à-dire verticalement sur l'axe des x et horizontalement sur l'axe des y.
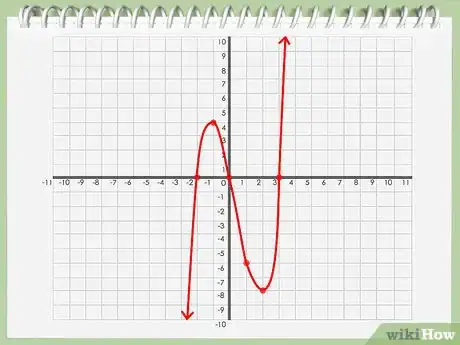
6
Représentez la courbe du polynôme. Une fois que vous avez marqué tous les points du graphique, vous pouvez relier les points pour obtenir une courbe continue de votre polynôme.
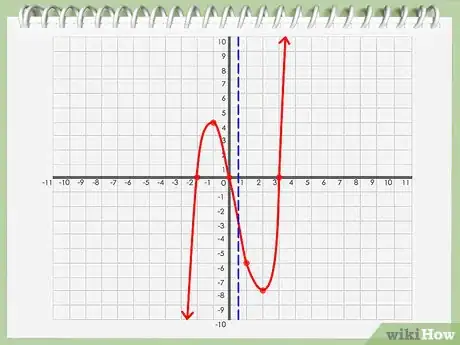
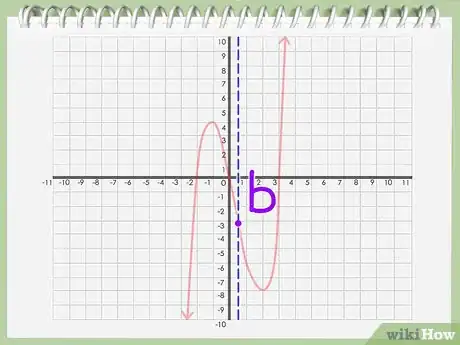
7
Recherchez l'axe de symétrie. Analysez bien votre graphique. Recherchez un point sur l'axe de telle sorte que la courbe soit divisée en deux parties égales lorsqu'une droite y passe de travers.
8
Marquez l'axe de symétrie. Si vous parvenez à déterminer un point (nommez-le « b ») sur l'axe des x qui divise la courbe en deux parties égales, alors ce point b est votre axe de symétrie.

Publicité

Conseils

Les longueurs de vos axes x et y devraient vous permettre d'avoir une idée globale de la forme de la courbe.
Certains polynômes ne sont pas symétriques. Par exemple, y = 3x n'a pas d'axe de symétrie.
La symétrie d'un polynôme peut être une symétrie paire ou impaire. Toute courbe qui a un axe de symétrie sur l'axe des y est dotée d'une symétrie dite « paire » et toute courbe ayant un axe de symétrie sur l'axe des x est dotée d'une symétrie « impaire ».