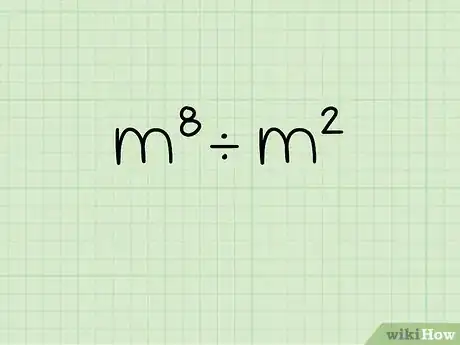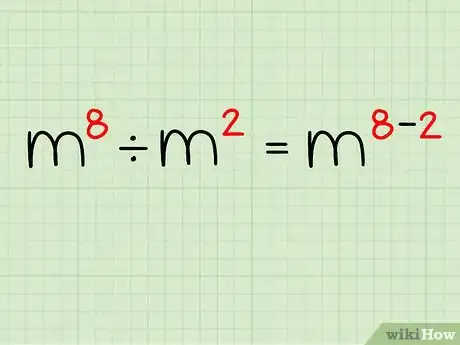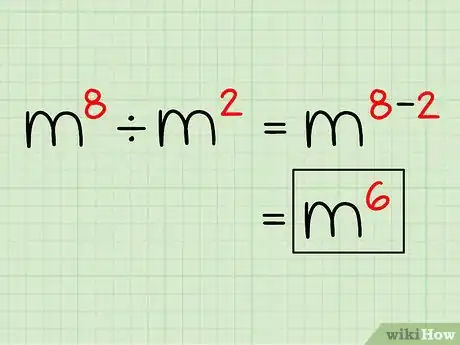Comment diviser des exposants

On pourrait croire qu'il est difficile de diviser, entre elles, des expressions comprenant des exposants. En fait, c'est plutôt simple à condition de travailler avec la même inconnue, mais avec des exposants différents. À y regarder de plus près, diviser des exposants revient à les soustraire ! C'est ce qu'on va vous expliquer dans les lignes qui suivent.

Méthode 1
Méthode 1 sur 2:
Quelques notions de base

  1. Image intitulée Divide Exponents Step 1
    1
    Posez le problème. On traitera ici des divisions du type : ma ÷ mb. Prenons l'exemple suivant : m8 ÷ m2. Écrivez cette opération sur votre feuille.
  2. Image intitulée Divide Exponents Step 2
    2
    Soustrayez le deuxième exposant du premier. Dans notre cas on soustrait 2 à 8. Cela nous donne désormais : m8 ÷ m2 = m8-2[1] .
  3. Image intitulée Divide Exponents Step 3
    3
    Donnez alors le résultat final. On fait l'opération : 8 - 2 = 6. La division de m8 par m2 donne : m6. Facile, non ? Si en lieu et place d'une inconnue vous avez une valeur, il faudrait calculer cette valeur. Ainsi si m = 2, la réponse finale est : 26 = 64.
    Publicité

Méthode 2
Méthode 2 sur 2:
Pour aller plus loin

  1. Image intitulée Divide Exponents Step 4
    1
    En cas de division, il faut vérifier qu'on travaille bien avec la même inconnue ou la même base. Si elles sont différentes (x et y par exemple), on ne peut rien calculer. Quelques explications.
    • Supposons qu'on vous demande faire l'opération suivante : m6 ÷ x4. Comme vous le voyez, les inconnues sont différentes, donc on ne peut rien faire.
    • Par contre, si, au lieu d'inconnues, on vous donne des nombres élevés à des puissances, il peut arriver qu'on puisse faire quelque chose, comme tout ramener à la même base. Soit l'opération : 23 ÷ 41. 4 est pair, donc 41 peut s'écrire aussi : 22, ce qui donne l'opération suivante : 23 ÷ 22 = 21, soit 2.
      • Cela ne marche que si la plus petite base est un multiple de la grande.
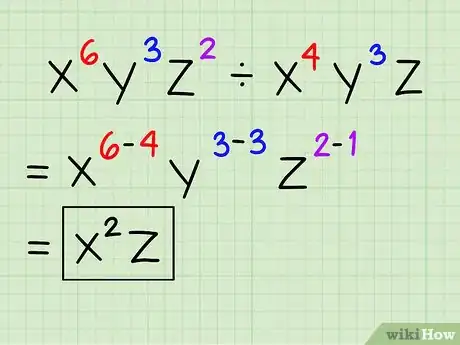
  2. Image intitulée Divide Exponents Step 5
    2
    Essayez de diviser des expressions ayant plusieurs inconnues différentes. Dans ce cas, vous divisez, entre elles, les inconnues identiques. Voyez plutôt l'exemple ci-dessous[2] .
    • x6y3z2 ÷ x4y3z =
    • x6-4y3-3z2-1 =
    • x2z
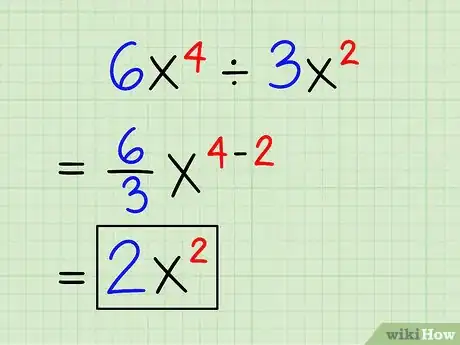
  3. Image intitulée Divide Exponents Step 6
    3
    Essayez de diviser des expressions ayant une seule inconnue, mais avec des coefficients. Une fois de plus, le principe général s'applique. Tant que vous avez la même inconnue, vous pouvez diviser (soustraction des exposants). Quant aux coefficients, s'ils peuvent se diviser, faites-le. Voyez plutôt l'exemple ci-dessous.
    • 6x4 ÷ 3x2 =
    • 6/3x4-2 =
    • 2x2
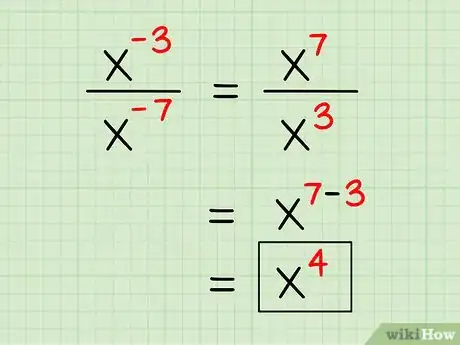
  4. Image intitulée Divide Exponents Step 7
    4
    Essayez de diviser des expressions ayant des exposants négatifs. Vous pouvez soit faire la division directement, le signe ne change rien au principe. Soit vous décidez de rendre ces exposants positifs. Il suffit pour cela de leur faire franchir la barre de division (dans un sens ou dans un autre). C'est ainsi que si 3-4 est le numérateur de la fraction, il devient 34 en dénominateur. Ci-dessous deux exemples[3] .
    • 1er exemple :
      • x-3/x-7 =
      • x7/x3 =
      • x7-3 =
      • x4
    • 2e exemple :
      • 3x-2y/xy =
      • 3y/(x2*xy) =
      • 3y/x3y =
      • 3/x3
    Publicité

Conseils

  • Il est de bon aloi de vérifier sa réponse avec une calculatrice. En cas d'inconnue, attribuez-lui une valeur (2 par exemple) et calculez la division de départ et l'expression simplifiée. Si les deux résultats sont identiques, c'est que vous avez juste.
  • Ce n'est pas grave de se tromper, ce qui compte, c'est d'essayer encore et encore !
Publicité

wikiHows en relation

calculer l'inverse d'une matrice 3x3
Comment
calculer l'inverse d'une matrice 3x3
calculer un pourcentage d'augmentation
Comment
calculer un pourcentage d'augmentation
calculer le diamètre d'un cercle
Comment
calculer le diamètre d'un cercle
calculer la hauteur d'un triangle
Comment
calculer la hauteur d'un triangle
calculer la valeur de résistances en série ou en dérivation
Comment
calculer la valeur de résistances en série ou en dérivation
calculer un écart type
Comment
calculer un écart type
calculer le déterminant d'une matrice 3 x 3
Comment
calculer le déterminant d'une matrice 3 x 3
calculer le rayon d’un cercle
Comment
calculer le rayon d’un cercle
calculer la diagonale d’un rectangle
Comment
calculer la diagonale d’un rectangle
calculer la longueur de l'hypoténuse
Comment
calculer la longueur de l'hypoténuse
calculer un intervalle de confiance
Comment
calculer un intervalle de confiance
calculer les probabilités de gagner à la loterie
Comment
calculer les probabilités de gagner à la loterie
calculer une racine carrée à la main
Comment
calculer une racine carrée à la main
calculer l’angle entre deux vecteurs
Comment
calculer l’angle entre deux vecteurs
Publicité

Références

  1. ↑ http://www.dummies.com/how-to/content/how-to-divide-exponents.html
  2. ↑ http://www.mathsisfun.com/algebra/variables-exponents-multiply.html
  3. ↑ http://www.purplemath.com/modules/simpexpo2.htm

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 11 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 16 246 fois.
Catégories: Calculs
Publicité