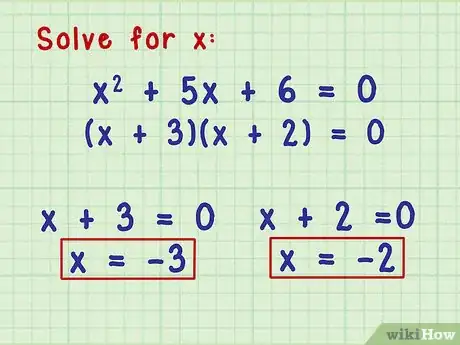Comment factoriser des équations algébriques

Informations concernant l'auteur.e

En mathématiques, factoriser revient à trouver les nombres ou expressions dont la multiplication donne un nombre donné ou une équation. La factorisation est une opération utile que vous devez connaitre pour pouvoir résoudre des problèmes algébriques basiques. L'habilité à bien factoriser devient presque indispensable lorsque vous avez affaire aux équations du second degré et autres formes de polynômes. La factorisation peut être utilisée pour simplifier des expressions algébriques pour rendre leur résolution plus simple. En factorisant, vous pouvez éliminer rapidement certaines expressions.

Méthode 1

Méthode 1 sur 3:
Factoriser les nombres et les expressions algébriques

1
Comprenez ce que c'est que la factorisation lorsqu'elle est appliquée à des nombres simples. La factorisation théoriquement parait simple, mais sa pratique peut s'avérer difficile surtout si vous avez affaire à des équations complexes. Pour cela, il est plus facile d'aborder le concept de factorisation en commençant avec les nombres simples, puis passer après aux équations simples avant d'essayer les opérations les plus compliquées. Les facteurs d'un nombre donné sont les nombres qui, multipliés entre eux, donnent le nombre en question. Par exemple, les facteurs de 12 sont 1 ; 12 ; 2 ; 6 ; 3 et 4, parce que 1 × 12 ; 2 × 6 et 3 × 4 donnent tous 12.
- Voici une autre façon d'y penser : les facteurs d'un nombre donné sont les nombres par lesquels le nombre est divisible.
- Pouvez-vous trouver tous les facteurs du nombre 60 ? Nous utilisons le nombre 60 pour plusieurs choses (les minutes dans une heure, les secondes dans une minute, etc.) parce qu'il est divisible par plusieurs nombres.
  - Les facteurs de 60 sont 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 et 60.
2
Sachez que les expressions variables peuvent aussi être factorisées. Tous comme les nombres simples, les expressions variables ayant des coefficients numériques peuvent aussi être factorisées. Savoir factoriser des variables est utile pour pouvoir simplifier des équations contenant des variables.
- Par exemple, la variable 12x peut être écrite comme un produit des facteurs 12 et x. Vous pouvez réécrire 12x comme 3(4x), 2(6x), etc., en utilisant n'importe quel facteur de 12 qui convient mieux dans vos opérations.
  - Nous pouvons aussi aller plus loin en factorisant l'expression 12x « plusieurs fois ». En d'autres termes, nous ne devons pas nous arrêter à 3(4x) ou 2(6x) – Nous pouvons factoriser 4x et 6x pour avoir respectivement 3(2(2x) et 2(3(2x). Ces deux expressions sont évidemment égales.
3
Appliquez la propriété distributive de la multiplication pour factoriser les équations algébriques. En utilisant vos connaissances de factorisation des nombres simples tout comme des variables avec coefficients, vous pouvez simplifier des équations algébriques simples en trouvant les facteurs que les nombres et les variables de l'équation ont en commun. Généralement, pour rendre l'équation aussi simple que possible, on essaie de trouver le plus grand facteur commun. Ce processus de simplification est possible grâce à la propriété distributive de la multiplication qui stipule que : pour tout nombre a, b et c, a(b + c) = ab + ac.
- Essayons un problème comme exemple. Pour factoriser l'équation algébrique 12x + 6, premièrement essayons de trouver le plus grand facteur commun de 12x et 6. 6 est le plus grand nombre qui divise éventuellement 12x et 6, alors nous pouvons simplifier l'équation, ce qui donne 6(2x + 1).
- Ce processus s'applique aussi pour les équations avec des nombres négatifs et des fractions. Par exemple, l'expression x/2 + 4 peut être simplifiée en 1/2(x + 8) et -7x + -21 peut être factorisé en -7(x + 3).
Publicité

Méthode 2

Méthode 2 sur 3:
Factoriser des équations du second degré

1
Assurez-vous que l'équation est sous la forme quadratique (ax² + bx + c = 0). Les équations du second degré sont sous la forme ax² + bx + c = 0, avec a, b et c des constantes numériques différentes de 0 (notez que a peut être égal à 1 ou -1). Si vous avez une équation contenant une variable (x) qui a un ou plusieurs termes de x à la seconde puissance, il est possible d'ajuster l'équation en utilisant les opérations algébriques basiques pour obtenir 0 d'un côté du signe égal de l'équation et ax², etc. de l'autre côté.
- Par exemple, considérons l'équation algébrique 5x² + 7x - 9 = 4x² + x - 18 qui peut être simplifiée en x² + 6x + 9 = 0, qui est sous la forme quadratique.
- Les équations ayant un x élevé à un nombre supérieur tel que x³, x⁴, etc. ne sont pas des équations quadratiques. Ce sont des équations du troisième degré, du quatrième degré et ainsi de suite, à moins qu'il soit possible de simplifier l'équation pour obtenir des termes de x élevés à la puissance 2.
2
Dans les équations du second degré où a = 1, vous pouvez les factoriser en (x+d )(x+e), où d × e = c et d + e = b. Si votre équation quadratique est sous la forme x² + bx + c = 0 (en d'autres termes, si le coefficient du terme x² = 1), il est possible (mais pas garanti) qu'un simple raccourci puisse être utilisé pour factoriser l'équation. Trouvez deux nombres qui, multipliés entre eux, donnent c et dont la somme donne b. Une fois que vous trouvez ces deux nombres d et e, placez-les dans l'expression suivante : (x+d)(x+e). Ces deux termes, lorsqu'ils sont multipliés ensemble donnent une équation, en d'autres termes, ce sont les facteurs de votre équation.
- Par exemple, considérons l'équation quadratique x² + 5x + 6 = 0. 3 et 2 multipliés ensemble donnent 6 et additionnés donnent 5, alors nous pouvons simplifier cette équation en (x + 3)(x + 2).
- Il existe de petites variations :
  - Si l'équation quadratique est sous la forme x²-bx+c, votre réponse sera sous la forme : (x - _)(x - _).
  - Sic'est sous la forme x²+bx+c, votre réponse sera sous la forme : (x + _)(x + _).
  - Si c'est sous la forme x²-bx-c, votre réponse sera sous la forme (x + _)(x - _).
- Note : les nombres représentés par les barres ( _ ) dans les parenthèses peuvent être des fractions tout comme des nombres décimaux. Par exemple, l'équation x² + (21/2)x + 5 = 0 se factorise en (x + 10)(x + 1/2).
3
Si possible, factorisez par identification. Croyez-y ou pas, pour des équations quadratiques qui ne sont pas compliquées, l'un des moyens de factorisation admis consiste juste à examiner le problème puis considérer des réponses probables jusqu'à ce que vous trouviez la bonne réponse. Si l'équation est sous la forme ax²+bx+c et a>1, votre réponse factorisée sera sous la forme (dx +/- _)(ex +/- _), avec d et e des constantes différentes de 0 dont la multiplication donnera a. d ou e (ou les deux) peuvent être égales à 1, bien que cela ne soit pas si nécessaire. Si les deux constantes sont égales à 1, vous avez certainement utilisé la méthode de raccourci décrite ci-dessus.
- Considérons cet exemple. 3x² - 8x + 4 à première vue semble difficile. Cependant, une fois que nous réalisons que 3 n'a que deux facteurs (3 et 1), ça devient plus facile, car nous savons que notre réponse doit être sous la forme (3x +/- _)(x +/- _). Dans ce cas, mettre un « -2 » à la place de la barre dans les deux parenthèses, nous donnera la bonne réponse. -2 × 3x = -6x et-2 × x = -2x. La somme de -6x et-2x donne -8x. -2 × -2 = 4, nous pouvons donc observer que les termes factorisés entre parenthèses se multiplient pour donner l'équation originale.
4
Résolvez le problème en complétant le carré. Dans certains cas, les équations quadratiques peuvent être rapidement et facilement résolues en utilisant une identité algébrique spéciale. Toute équation quadratique sous la forme x² + 2xh + h² = (x + h)². Alors, si dans votre équation, la valeur de b est le double de la racine carrée de la valeur de c, votre équation peut être factorisée en (x + (sqrt(c)))².
- Par exemple, dans l'équation x² + 6x + 9, on sait que 3² = 9 et 3 × 2 = 6. Dès lors, nous savons que la forme factorisée de cette équation est (x + 3)(x + 3) ou (x + 3)².
5
Utilisez des facteurs pour résoudre les équations quadratiques. Indépendamment de la façon dont vous factorisez l'équation quadratique, une fois factorisée, vous pouvez trouver des réponses probables de la valeur de x en posant toute l'expression égale à 0 et en résolvant. Puisque vous recherchez des valeurs de x qui annule l'équation, une valeur de x qui annule l'un des facteurs de l'équation est probablement une réponse pour votre équation quadratique.
- Reprenons l'équation x² + 5x + 6 = 0. Sa factorisation donne (x + 3)(x + 2) = 0. Si l'un des facteurs est égal à 0, l'équation entière est égale à 0, alors les valeurs probables de x sont les nombres qui annulent (x + 3) et (x + 2). Ces nombres sont respectivement -3 et -2.
6
Vérifiez vos réponses - certaines peuvent être bizarres. Si vous trouvez les réponses probables de x, replacez-les dans l'équation originale pour voir si c'est correct. Des fois, les réponses que vous trouvez n'annulent pas l'équation originale lorsque vous la replacez dans l'équation originale. Nous appelons ces réponses des réponses « étranges » et ne les considérons pas.
- Plaçons -2 et -3 dans x² + 5x + 6 = 0. Premièrement, -2 :
  - (-2)² + 5(-2) + 6 = 0
  - 4 + -10 + 6 = 0
  - 0 = 0. C'est correct, donc -2 est une réponse valide.
- Maintenant essayons -3 :
  - (-3)² + 5(-3) + 6 = 0
  - 9 + -15 + 6 = 0
  - 0 = 0. Ceci est aussi correct, donc -3 est aussi une réponse valide.
Publicité

Méthode 3

Méthode 3 sur 3:
Factoriser d'autres formes d'équations

1
Si l'équation est sous la forme a²-b², factorisez-la en (a+b)(a-b). La factorisation des équations à deux variables est différente de celle des équations quadratiques basiques. Pour toute équation a²-b² avec a et b différents de 0, la factorisation de l'équation donne (a+b)(a-b).
- Par exemple, l'équation 9x² - 4y² = (9x + 4y)(9x - 4y).
2
Si l'équation est sous la forme a²+2ab+b², factorisez-la en (a+b)². Notez que si le trinôme est sous la forme a²-2ab+b², la forme factorisée diffère un peu : (a-b)².
- L'équation 2x² + 16xy + 4y² peut être réécrite comme 2x² + (2 × 2 × 4)xy + 4y². C'est sous la forme correcte, donc nous pouvons affirmer tout confiant que la factorisation de l'équation donne (2x + 4y)²
3
Si l'équation est sous la forme a³-b³, factorisez-la en (a-b)(a²+ab+b²). Finalement, il convient de mentionner que les équations du troisième degré et de degrés supérieurs peuvent être factorisées même si le processus de factorisation à ce niveau devient plus compliqué.
- Par exemple, la factorisation de 2x² - 3y² donne (2x - 3y)(2x² + ((2x)(3y)) + 3y²)
Publicité

Conseils

a²-b² est factorisable, a²+b² ne l'est pas.
Gardez en tête comment factoriser des constantes, cela pourrait vous aider.
Prenez garde aux fractions dans le processus de factorisation. Travaillez avec les fractions de façon correcte.
Si vous avez un trinôme sous la forme x²+bx+ (b/2)², la forme factorisée serait (x+(b/2))².
Souvenez-vous que a0 = 0 (0 est élément absorbant pour la multiplication).