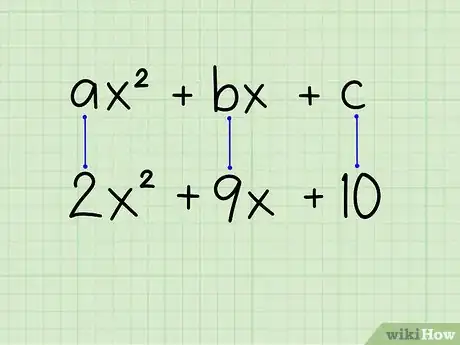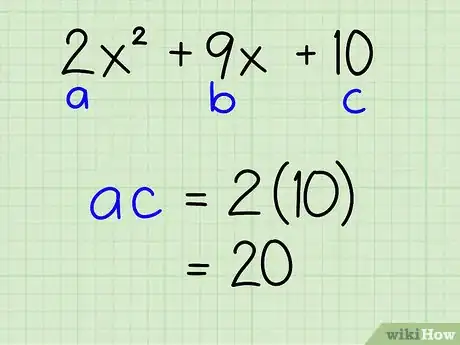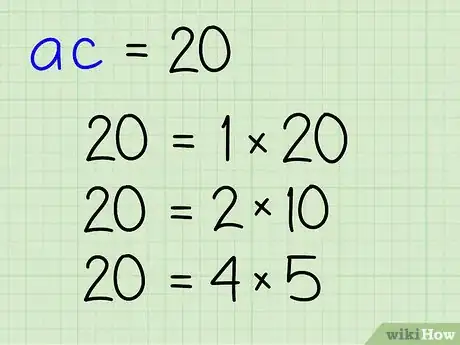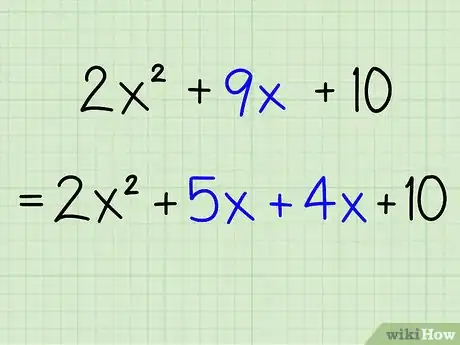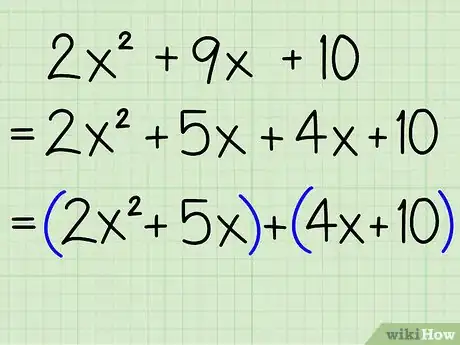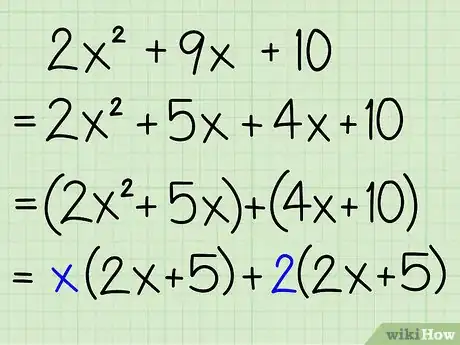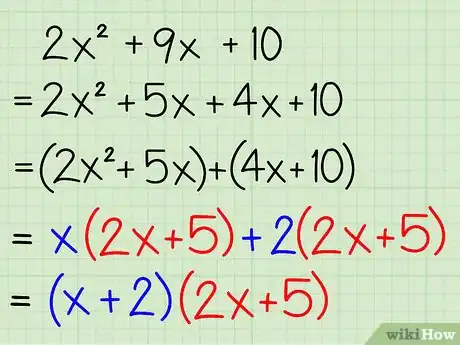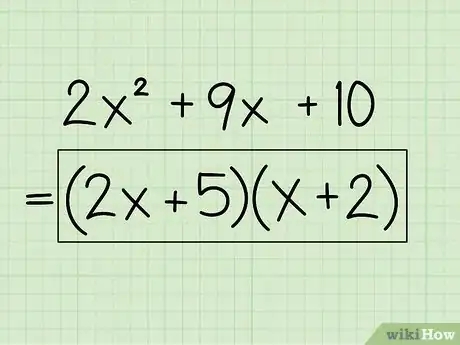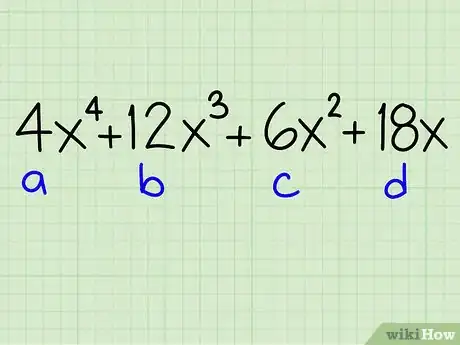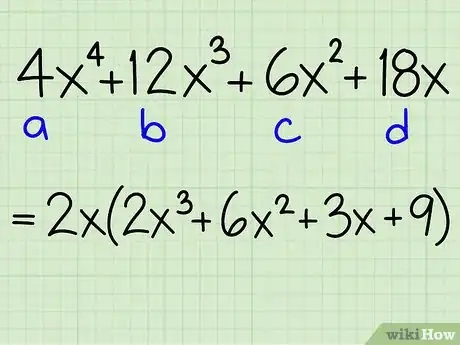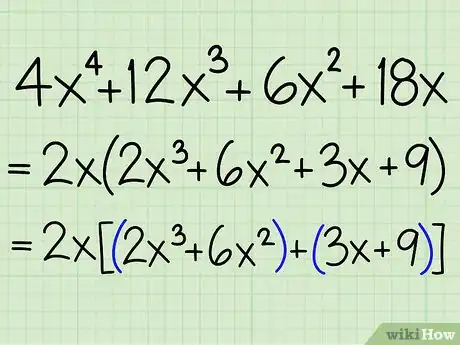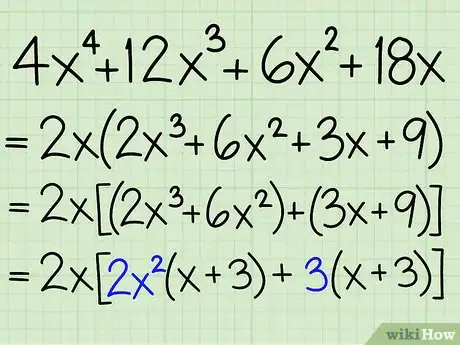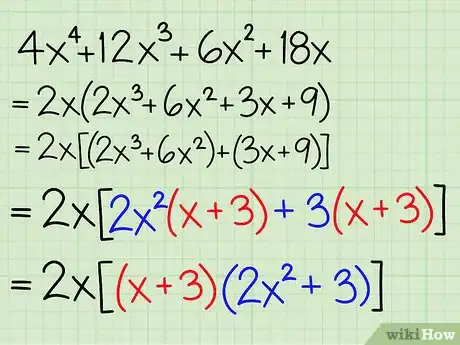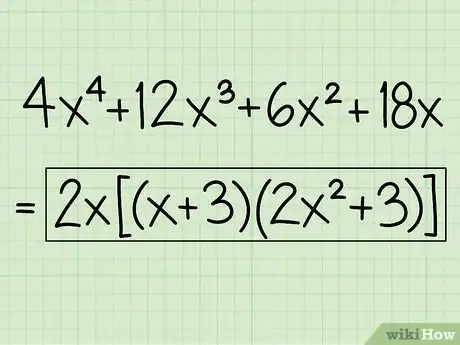Comment factoriser par groupement

Il existe une technique qui permet de résoudre plus facilement les équations du second degré, celle des groupements. Elle sert également dans la simplification des polynômes à quatre termes. Il existe de légères variations de méthode selon le type de polynômes.

Méthode 1
Méthode 1 sur 2:
Factoriser des polynômes du second degré [1] [2]

  1. Image intitulée Factor by Grouping Step 1
    1
    Commencez par observer la structure du polynôme. Avec cette méthode, il faut que le polynôme se présente obligatoirement sous sa forme canonique : ax2 + bx + c
    • Le plus souvent, on pense à utiliser cette méthode quand le premier coefficient (le "a" de ax2) est différent de 1, mais la méthode marche quand même dans ce cas.
    • Exemple : 2x2 + 9x + 10
  2. Image intitulée Factor by Grouping Step 2
    2
    Trouvez le produit des coefficients extrêmes. Multipliez les coefficients a et c. Ce produit s'appelle le produit des coefficients extrêmes.
    • Exemple : 2x2 + 9x + 10
      • a = 2 ; c = 10
      • a x c = 2 x 10 = 20
  3. Image intitulée Factor by Grouping Step 3
    3
    Décomposez le produit des coefficients extrêmes en paires de facteurs. Dressez la liste de tous les facteurs de ce dernier produit, puis groupez-les par paires dont le produit donne le produit des coefficients.
    • Exemple : les facteurs de 20 sont : 1, 2, 4, 5, 10, 20
      • On obtient ainsi les paires de facteurs uniques : (1, 20), (2, 10), (4, 5)
  4. Image intitulée Factor by Grouping Step 4
    4
    Trouvez ensuite la paire de facteurs dont la somme est égale au deuxième coefficient du polynôme, c'est-à-dire "b". Prenez chacune des paires et additionnez les deux éléments, vous devez sélectionner la paire dont la somme est le coefficient "b".
    • Si votre produit des coefficients extrêmes est négatif, il vous faudra trouver la paire dont la différence est égale au coefficient "b".
    • Exemple : 2x2 + 9x + 10
      • b = 9
      • 1 + 20 = 21 – ce n'est pas la bonne paire
      • 2 + 10 = 12 – ce n'est pas la bonne paire
      • 4 + 5 = 9 – c'est la bonne paire
  5. Image intitulée Factor by Grouping Step 5
    5
    Remplacez le coefficient du deuxième terme du polynôme par la paire que vous avez trouvée. Développez le nouveau terme, en faisant attention aux signes.
    • Peu importe le sens des facteurs dans la paire, puisque a + b = b + a.
    • Exemple : 2x2 + 9x + 10 = 2x2 + (5 + 4)x + 10 = 2x2 + 5x + 4x + 10
  6. Image intitulée Factor by Grouping Step 6
    6
    Regroupez les quatre termes en deux paires de termes. Groupez les deux premiers, puis les deux derniers.
    • Exemple : 2x2 + 5x + 4x + 10 = (2x2 + 5x) + (4x + 10)
  7. Image intitulée Factor by Grouping Step 7
    7
    Factorisez chacune des paires. Trouvez à l'intérieur de chaque paire le ou les facteurs communs, et mettez-les en facteurs. Récrivez alors le polynôme.
    • Exemple : x(2x + 5) + 2(2x + 5) — on a mis "x" en facteur pour la première paire et 2, pour la seconde
  8. Image intitulée Factor by Grouping Step 8
    8
    Factorisez à nouveau. Normalement, vous devriez pouvoir factoriser les deux termes entre parenthèses, car ils devraient être identiques. Pour finir, vous mettrez ensemble les termes restants..
    • Exemple : (2x + 5)(x + 2) — on met (2x + 5) en facteur et on groupe le reste
  9. Image intitulée Factor by Grouping Step 9
    9
    Inscrivez votre réponse finale.
    • Exemple : 2x2 + 9x + 10 = (2x + 5)(x + 2)
      • La réponse finale est : (2x + 5)(x + 2)
    Publicité

Exemples de factorisation de polynômes du second degré

  1. Image intitulée Factor by Grouping Step 10
    1
    Factorisez : 4x2 - 3x - 10
    • a x c = 4 x -10 = -40
    • Les paires de facteurs de 40 sont : (1, 40), (2, 20), (4, 10), (5, 8)
    • La bonne paire est : (5, 8); 5 - 8 = -3
    • 4x2 - 8x + 5x - 10
    • (4x2 - 8x) + (5x - 10)
    • 4x(x - 2) + 5(x - 2)
    • (x - 2)(4x + 5)
  2. Image intitulée Factor by Grouping Step 11
    2
    Factorisez : 8x2 + 2x - 3
    • a x c = 8 x -3 = -24
    • Les paires de facteurs de 24 sont : (1, 24), (2, 12), (4, 6)
    • La bonne paire est : (4, 6), puisque 6 - 4 = 2
    • 8x2 + 6x - 4x - 3
    • (8x2 + 6x) - (4x + 3)
    • 2x(4x + 3) - 1(4x + 3)
    • (4x + 3)(2x - 1)
    Publicité

Méthode 2
Méthode 2 sur 2:
Factoriser des polynômes ayant quatre termes [3] [4]

  1. Image intitulée Factor by Grouping Step 12
    1
    Commencez par observer la structure du polynôme. Il doit présenter quatre termes. Les polynômes de ce type peuvent être très différents, ainsi que vous le verrez par la suite.
    • Le plus souvent, on utilise cette méthode avec les polynômes du troisième degré du type : ax3 + bx2 + cx + d
    • Les polynômes doivent se présenter sous leurs formes canoniques. Exemples :
      • axy + by + cx + d
      • ax2 + bx + cxy + dy
      • ax4 + bx3 + cx2 + dx
      • …ou d'autres formes.
    • Exemple : 4x4 + 12x3 + 6x2 + 18x
  2. Image intitulée Factor by Grouping Step 13
    2
    Trouvez le plus grand commun facteur (PGCF) et mettez-le en facteur. Voyez s'il y a un facteur commun à tous les termes du polynôme. Trouvez le plus grand possible, s'il y en a un, et mettez-le en facteur.
    • Si le PGCF est 1, il n'y a rien à faire, vous ne pouvez pas factoriser.
    • Quand vous aurez factorisé le PGCF, il ne faudra pas le perdre en cours de calcul sous prétexte qu'il se trouve à part. Il faudra le récrire chaque fois jusqu'à la réponse finale.
    • Exemple : 4x4 + 12x3 + 6x2 + 18x
      • 2x est commun à chacun des termes, on peut donc le mettre en facteur, ce qui donne :
      • 2x(2x3 + 6x2 + 3x + 9)
  3. Image intitulée Factor by Grouping Step 14
    3
    Regroupez ensuite les termes qui ont un ou des facteurs en commun. Par exemple, vous pouvez grouper les deux premiers termes et les deux derniers.
    • Si le premier terme du second groupe est négatif, mettez -1 en facteur. Ainsi, le premier terme devient positif et il vous faudra changer le signe du deuxième terme (+ deviendra -, et vice-versa)
    • Exemple : 2x(2x3 + 6x2 + 3x + 9) = 2x[(2x3 + 6x2) + (3x + 9)]
  4. Image intitulée Factor by Grouping Step 15
    4
    Trouvez le plus grand commun facteur (PGCF) de chaque binôme. Ces PGCF devront se trouver, comme il se doit, devant la parenthèse du binôme en question. Récrivez le polynôme en conséquence.
    • Quand on factorise, 2x par exemple, on doit se demander si on factorise 2x ou -2x. Tout dépend en fait des signes des termes du binôme. Il y a deux cas de figure :
      • Si le premier terme du binôme est positif, on factorisera une quantité positive.
      • Si le premier des termes est négatif, on factorisera une quantité négative.
    • Exemple : 2x[(2x3 + 6x2) + (3x + 9)] = 2x2[2x2(x + 3) + 3(x + 3)] — on a mis 2x2 en facteur sur le premier binôme et seulement 3 sur le second.
  5. Image intitulée Factor by Grouping Step 16
    5
    Factorisez à nouveau le binôme commun. Normalement, vous devez voir apparaitre un binôme commun, et comme tel, vous pouvez le mettre en facteur commun. Il suffit ensuite d'arranger le polynôme en conséquence. Attention à ne rien oublier et à ne pas changer les signes !
    • Si vous n'obtenez pas deux binômes identiques, c'est qu'il y a eu une erreur quelque part. Refaites vos calculs. Il s'agit peut-être simplement d'une mauvaise disposition des termes ou d'un manque de simplification.
    • Ce qui est entre parenthèses, les deux derniers binômes doivent être identiques. Si ce n'est pas le cas, c'est tout simplement que le polynôme ne peut pas être factorisé ni avec cette méthode ni avec aucune autre d'ailleurs.
    • Exemple : 2x2[2x2(x + 3) + 3(x + 3)] = 2x2[(x + 3)(2x2 + 3)]
  6. Image intitulée Factor by Grouping Step 17
    6
    Inscrivez votre réponse. Arrivé à ce stade, vous devez avoir votre réponse définitive.
    • Exemple : 4x4 + 12x3 + 6x2 + 18x = 2x2(x + 3)(2x2 + 3)
      • Votre réponse finale est donc : 2x2(x + 3)(2x2 + 3)
    Publicité

Exemples de factorisation de polynômes à quatre termes

  1. Image intitulée Factor by Grouping Step 18
    1
    Factorisez : 6x2 + 2xy - 24x - 8y
    • 2[3x2 + xy - 12x - 4y]
    • 2[(3x2 + xy) - (12x + 4y)]
    • 2[x(3x + y) - 4(3x + y)]
    • 2[(3x + y)(x - 4)]
    • 2(3x + y)(x – 4)
  2. Image intitulée Factor by Grouping Step 19
    2
    Factorisez : x3 - 2x2 + 5x - 10
    • (x3 - 2x2) + (5x - 10)
    • x2(x - 2) + 5(x - 2)
    • (x - 2)(x2 + 5)
    Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ http://www.mathwarehouse.com/algebra/polynomial/how-to-factor-by-grouping.php
  2. ↑ http://www.regentsprep.org/Regents/math/algtrig/ATV1/revFactorGrouping.htm
  3. ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut27_gcf.htm
  4. ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/factoring/grouping/grouping.html

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, des auteur.e.s volontaires ont participé à l'édition et à l'amélioration. Cet article a été consulté 8 316 fois.
Catégories: Mathématiques
Publicité