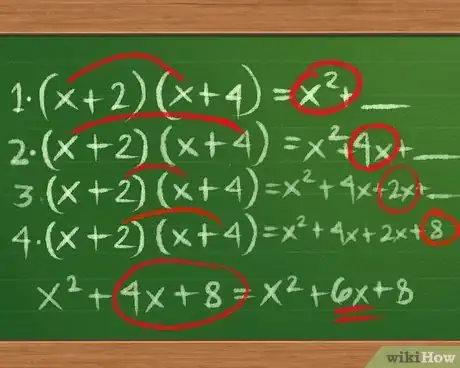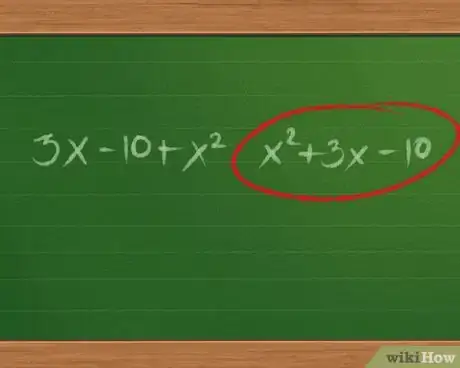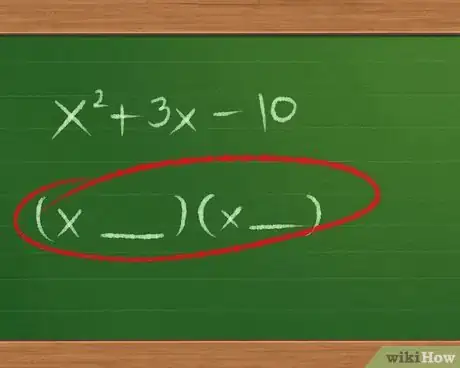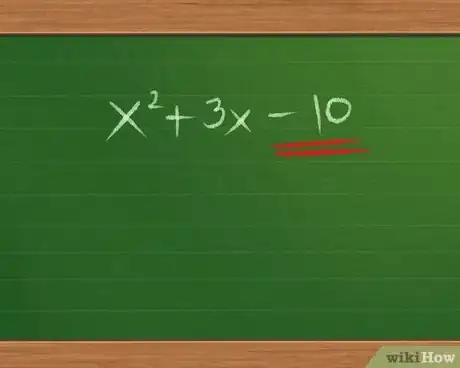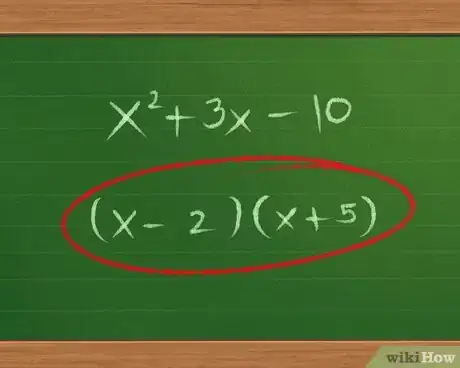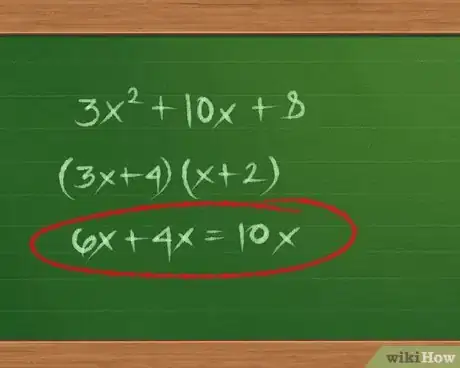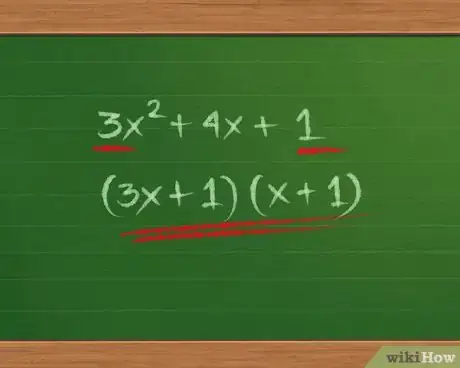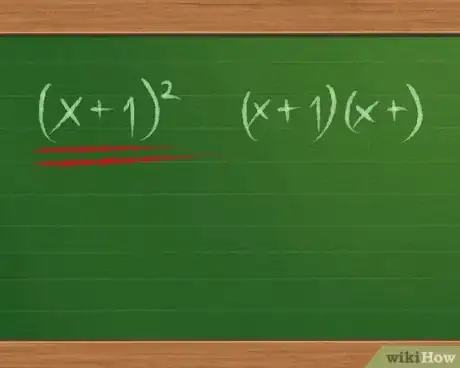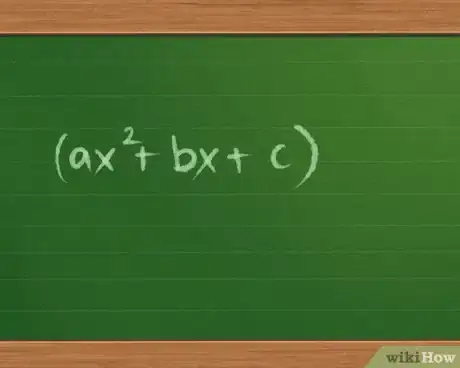wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 14 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 33 861 fois.
Comme son nom l'indique, un trinôme est une expression mathématique qui se présente sous la forme d'une somme de trois termes. Le plus souvent, on commence à étudier les trinômes du second degré qui s'écrivent ainsi : ax2 + bx + c. Il existe plusieurs façons de factoriser un trinôme du second degré. Avec de la pratique, vous y arriverez sans difficulté. Les méthodes que l'on va voir ne s'appliquent pas aux trinômes d'un degré supérieur (avec x3 ou x4). Cependant, on peut, en travaillant ces derniers trinômes, retomber sur des trinômes du second degré. On voit tout cela en détail.
Étapes
Partie 1
Partie 1 sur 3:Apprendre à factoriser x2 + bx + c
-
1Utilisez la méthode PEID. Vous la connaissez peut-être, mais rappelons ici de quoi il retourne. Quand vous devez développer un produit de binômes - (x+2)(x+4), par exemple - il faut faire la somme des produits des différents termes dans l'ordre « Premier, Externe, Interne, Dernier ». En détail, cela donne :
- multipliez les Premiers termes entre eux : (x+2)(x+4) = x2 + __
- multipliez les termes Externes entre eux : (x+2)(x+4) = x2 + 4x + __
- multipliez les termes Internes entre eux : (x+2)(x+4) = x2 + 4x + 2x + __
- multipliez les Derniers termes entre eux : (x+2)(x+4) = x2 + 4x + 2x + 8
- Terminez en simplifiant : x2 + 4x + 2x + 8 = x2 + 6x + 8
-
2Comprenez bien ce qu'est la factorisation. Quand vous développez le produit de deux binômes, vous obtenez un trinôme de la forme : ax2+bx+c, a, b et c étant des nombres réels. Quand on fait l'opération inverse, passer du trinôme au produit de binômes, on dit qu'on factorise.
- Pour plus de clarté, il faut classer les termes d'un trinôme par ordre de puissance décroissante. Ainsi, si on vous donne : 3x - 10 + x2, il faut récrire dans l'ordre : x2 + 3x - 10.
- Le plus grand exposant étant 2 (x2), on parle de trinôme du « second degré ».
-
3Au début de la factorisation, on pose la forme du produit de binômes. Écrivez : (__ __)(__ __). On remplira au fur et à mesure les espaces laissés libres, ainsi que les signes.
- Pour l'instant on ne met aucun signe (+ ou -) entre les deux termes des binômes.
-
4Vous devez commencer par trouver les premiers termes de chaque binôme. Si votre trinôme commence par x2, les deux premiers termes des binômes seront forcément x et x, puisque x fois x = x2.
- Notre trinôme de départ étant : x2 + 3x - 10 et comme il n'y a pas de coefficient à x2, on peut immédiatement inscrire :
- (x __)(x __)
- Nous verrons plus loin comment on procède lorsque le coefficient de x2 est différent de 1, comme 6x2 ou -x2. Pour l'instant, on en reste à ce cas simple.
-
5Essayez de deviner quels seront les derniers termes des binômes. Relisez comment, avec la méthode PEID, on a développé les derniers termes des binômes. Nous devons à présent faire l'inverse. On a donc multiplié les deux derniers termes pour obtenir le dernier terme (« constante ») du trinôme. Donc, vous allez devoir trouver deux nombres qui, multipliés entre eux, vous donneront la constante du trinôme.
- Dans notre exemple : x2 + 3x - 10, la constante est -10.
- Quels sont les facteurs de -10 ? Quels sont les deux nombres qui, multipliés entre eux, vous donneront -10 ?
- Voici tous les cas possibles : -1 x 10, 1 x -10, -2 x 5 et 2 x -5. Inscrivez ces combinaisons quelque part pour vous en souvenir.
- Pour l'instant, votre produit de binômes reste inchangé. Il ressemble toujours à : (x __)(x __).
-
6Testez les différentes combinaisons. À partir de la constante, vous avez réussi à dégager quelques combinaisons de facteurs, dont l'une doit marcher (si le trinôme est réductible). À ce stade, il n'existe pas d'autres solutions que d'essayer chacune des combinaisons pour voir si l'une d'elles satisfait au trinôme. Par exemple :
- Dans notre exemple, il faut que la somme du produit « Externe » et du produit « Interne » donne 3x (tiré de x2 + 3x - 1)
- Prenons la combinaison -1 et 10 : (x - 1)(x + 10). La somme du produit « Externe » et du produit « Interne » donne : 10x - x = 9x. Cela ne marche pas !
- Prenons la combinaison 1 et -10 : (x + 1)(x - 10). La somme du produit « Externe » et du produit « Interne » donne : -10x + x = -9x. Cela ne va toujours pas ! Vous remarquerez au passage que cette dernière vérification était inutile. En effet, la paire (-1,10) donne 9x et la paire (1, -10) donne -9x. Il suffit donc de tester une seule paire.
- Prenons la combinaison -2 et 5 : (x - 2)(x + 5). La somme du produit « Externe » et du produit « Interne » donne : 5x - 2x = 3x. Eurêka ! La réponse est donc : (x - 2)(x + 5).
- Dans le cas de trinômes aussi simples que celui-ci (commençant par x2), on peut faire plus court. Il suffit d'additionner les deux facteurs potentiels, vous rajoutez « x » à la fin et vous voyez tout de suite si c'est la bonne combinaison. Là, vous faites : -2 + 5 → 3x. Si x2 est flanqué d'un coefficient, alors la méthode ne marche pas, c'est pourquoi il est bon de se souvenir la méthode détaillée.
Publicité
Partie 2
Partie 2 sur 3:Apprendre à factoriser des trinômes plus compliqués
-
1Factorisez votre trinôme pour aboutir à un trinôme plus simple. Admettons que vous ayez à factoriser le trinôme suivant : 3x2 + 9x - 30. Essayez de voir s'il n'y aurait pas un diviseur commun aux trois termes. On prend alors le plus grand (s'il y en a plusieurs), d'où son nom de « Plus Grand Commun Diviseur » (ou PGCD) [1] . Dans notre trinôme, ce sera 3. Voyons cela en détail :
- 3x2 = (3)(x2)
- 9x = (3)(3x)
- -30 = (3)(-10)
- Ainsi, 3x2 + 9x - 30 = (3)(x2 + 3x - 10). Dès lors, il est facile de factoriser la deuxième parenthèse selon la méthode décrite plus haut. On obtient ainsi : (3)(x-2)(x+5). Il ne faut pas oublier le 3 mis en facteur.
-
2Il arrive qu'on puisse mettre en facteur non pas des nombres réels, mais des quantités avec des inconnues. Ainsi on peut mettre en facteur des « x », des « y » ou des « xy ». Voici quelques exemples :
- 2x2y + 14xy + 24y = (2y)(x2 + 7x + 12)
- x4 + 11x3 - 26x2 = (x2)(x2 + 11x - 26)
- -x2 + 6x - 9 = (-1)(x2 - 6x + 9)
- Ensuite, il faut, bien sûr, factoriser le nouveau trinôme comme on l'a vu précédemment. Faites quand même une vérification pour voir s'il n'y a pas d'erreurs. Exercez-vous avec les exercices proposés à la fin de cet article.
-
3Tentez de factoriser des trinômes avec un x2 flanqué d'un coefficient. Certains trinômes du second degré sont plus difficiles à factoriser, à l'image de 3x2 + 10x + 8. On va voir comment on procède, ensuite de quoi vous pourrez vous entraîner avec les exercices proposés en fin d'article. Voici donc comment on opère :
- Posez le produit de binômes : (__ __)(__ __)
- Chacun des deux « Premiers » termes doit comporter un « x » et le produit des deux doit donner 3x2. Il n'y a qu'une possibilité : (3x __)(x __), 3 étant un nombre premier.
- Trouvez les facteurs de 8. Il y a deux possibilités : 1 x 8 ou 2 x 4.
- Prenez ces combinaisons pour trouver les constantes des binômes. Point important : comme l'inconnue « x » a des coefficients différents, l'ordre de la combinaison a son importance. Vous devez trouver au final le terme du milieu, ici, 10x. Voici les différentes combinaisons :
- (3x+1)(x+8) → 24x + x = 25x non !
- (3x+8)(x+1) → 3x + 8x = 11x non !
- (3x+2)(x+4) → 12x + 2x =14x non !
- (3x+4)(x+2) → 6x + 4x = 10x oui ! C'est la bonne factorisation.
-
4En présence d'une inconnue ayant une puissance supérieure à 2, on peut créer une inconnue de substitution. Un jour, vous aurez certainement à factoriser un trinôme du quatrième (x4) ou du cinquième degré (x5). L'objectif est de ramener ce trinôme à quelque chose de connu, c'est-à-dire un trinôme du second degré afin de pouvoir factoriser sans problème. Par exemple :
- x5 + 13x3 + 36x
- = (x)(x4 + 13x2 + 36)
- Inventez une nouvelle inconnue qui va simplifier le problème. On posera ici que Y = x2. On met un Y majuscule pour ne pas oublier que c'est une inconnue de substitution. Le trinôme devient alors :
- = (x)(Y2 + 13Y + 36) : on factorise comme dans la partie 1.
- = (x)(Y + 9)(Y + 4). Il est temps de remplacer l'inconnue de substitution par sa véritable valeur :
- = (x)(x2 + 9)(x2 + 4)
- = (x)(x + 3)(x - 3)(x + 2)(x - 2)
Publicité
Partie 3
Partie 3 sur 3:Quelques cas particuliers de factorisations de trinômes
-
1Recherchez d'éventuels nombres premiers. Voyez si la constante et/ou le coefficient du premier ou du troisième terme ne seraient pas des nombres premiers. Rappelons qu'un nombre est dit « premier » quand il n'est divisible que par 1 ou lui-même. Partant de cette définition, si on trouve un nombre premier aux places indiquées ci-dessus, le trinôme ne pourra se factoriser que sous la forme d'un seul produit de binômes.
- Par exemple, dans x2 + 6x + 5, la constante 5 est un nombre premier, donc le produit de binômes sera de la forme : (__ 5)(__ 1)
- Dans 3x2 + 10x + 8, le coefficient 3 est un nombre premier, donc le produit de binômes sera de la forme : (3x __)(x __).
- Enfin, dans 3x2 + 4x + 1, 3 et 1 étant des nombres premiers, la seule solution possible est : (3x + 1)(x + 1). Cependant, il faut toujours vérifier la combinaison. Il arrive que certains trinômes ne puissent être factorisés. Ainsi, 3x2 + 100x + 1 ne peut être factorisé (on dit qu'il est « irréductible »). Avec 3 et 1, vous n'obtiendrez jamais 100.
-
2Il faut toujours penser au cas d'un trinôme qui serait le développement d'une identité remarquable, un carré parfait pour ne prendre que cet exemple. Par carré parfait, on entend le produit des deux binômes parfaitement identiques : (x + 1)(x + 1) qu'on écrit (x + 1)2. Voici quelques-uns de ces carrés parfaits :
- x2 + 2x + 1 = (x+1)2 et x2 - 2x + 1 = (x - 1)2
- x2 + 4x + 4 = (x + 2)2 et x2 - 4x + 4 = (x - 2)2
- x2 + 6x + 9 = (x + 3)2 et x2 - 6x + 9 = (x - 3)2
- Un trinôme ax2 + bx + c est le développement d'un carré parfait si a et c sont eux-mêmes des carrés positifs (comme 1, 4, 9, 16, 25…) et si b (positif ou négatif) est égal à 2(√a x √c) = 2 √ac [2] .
-
3Voyez s'il est possible de factoriser. En effet, iI est des trinômes qui ne peuvent être factorisés. Si vous peinez à factoriser un trinôme du second degré de forme canonique ax2 + bx + c, parce qu'il n'y a pas de racines évidentes, il faut recourir à la méthode du discriminant (Δ). Ce dernier se calcule ainsi : Δ = √b2 - 4ac. Si Δ < 0, alors le trinôme ne peut être factorisé.
- Pour les trinômes qui ne sont pas du second degré, utilisez le critère d'Eisenstein expliqué dans la section « Conseils ».
Publicité
Exercices résolus et à faire
- Exemples de factorisation après une mise en facteur : on a évoqué plus haut ce genre de problème où il fallait d'abord mettre une certaine quantité en facteur pour pouvoir factoriser le reste. Résolvez les trois exemples qui ont déjà été traités et contrôlez votre réponse ensuite :
- Problème : 2x2y + 14xy + 24y → solution : (2y)(x2 + 7x + 12) = (2y)(x+3)(x+4)
- Problème : x4 + 11x3 - 26x2 → solution : (x2)(x2 + 11x - 26) = (x2)(x + 13)(x - 2)
- Problème : -x2 + 6x - 9 → solution : (-1)(x2 - 6x + 9) = (x - 3)(x - 3) = (-1)(x - 3)2
- Exemples de factorisation après une mise en facteur : ces problèmes sont nouveaux et nous ne vous donnons pas la réponse tout de suite. Sachez que vous devez donc mettre une quantité en facteur, puis factorisez le trinôme qui reste. La solution se trouve entre le trinôme et la flèche : il vous suffira de surligner cet espace avec la souris :
- 3x3 + 3x2 - 6x = (3x)(x + 2)(x - 1) ← sélectionnez cet espace en blanc avec la souris pour découvrir la solution.
- -5x3y2 + 30x2y2 - 25y2x = (-5xy2)(x -5)(x - 1) ← sélectionnez cet espace en blanc avec la souris pour découvrir la solution.
-
Exemples de factorisation un peu plus complexes ou originales : ici, les racines sont loin d'être évidentes, mais, avec un peu de réflexion et par tâtonnements, on peut arriver à factoriser sous la forme (_x + __)(_x + __) :
- 2x2 + 3x - 5 = (2x + 5)(x - 1) ← sélectionnez cet espace en blanc avec la souris pour découvrir la solution.
- 9x2 + 6x + 1 = (3x + 1)(3x + 1)=(3x + 1)2 ← sélectionnez cet espace en blanc avec la souris pour découvrir la solution (petit coup de pouce : 9x offre plusieurs combinaisons de facteurs)
Conseils
- Si vous n'arrivez pas à factoriser facilement un trinôme du second degré de forme ax2+bx+c, il faut recourir à la méthode du discriminant (Δ) pour savoir si le trinôme est factorisable ou non.
- Dans le cadre de la factorisation des polynômes d'un degré supérieur à 2, on peut utiliser le « critère d'Eisenstein ». Ce théorème s'applique à tous les polynômes, mais s'applique particulièrement bien aux trinômes, puisque la plupart des coefficients sont, dès lors, nuls. Ce n'est pas une technique de factorisation, mais il permet de savoir rapidement si un polynôme est irréductible ou non. Selon ce critère, s'il existe un entier p qui divise exactement b et c (les deux derniers termes d'un polynôme) et si les conditions ci-dessous sont remplies, alors le polynôme est irréductible. Voici ces deux conditions :
- la constante c est un multiple de p, mais pas de p2
- le coefficient a (de ax2+bx+c) n'est pas multiple de p
- par exemple, 14x2 + 45x + 51 est irréductible, car il y a bien un nombre premier (3) qui divise exactement 45 et 51, mais pas 14. De plus, 51 n'est pas divisible par 9, soit 32
Avertissements
- Attention ! Les trinômes factorisables ne le sont pas forcément sous la forme du produit de deux binômes. Ainsi, x4 + 105x + 46 = (x2 + 5x + 2)(x2 - 5x + 23). Avec du second degré, c'est toujours le produit de deux binômes.
Références
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut28_facttri.htm
- ↑ http://www.themathpage.com/alg/perfect-square-trinomial.htm
- http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut28_facttri.htm
- http://www.themathpage.com/alg/factoring-trinomials.htm
- http://www.algebrahelp.com/lessons/factoring/trinomial/