Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 8 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 12 507 fois.
Il est parfois difficile de faire des démonstrations. Pour y parvenir, il faut mettre en œuvre à la fois ses connaissances en mathématiques et le savoir-faire propre à la rédaction de cette démonstration. Malheureusement, il n’existe pas de méthode magique pour réussir sans effort et du premier coup. Vous devez avoir des bases solides dans cette matière pour nourrir votre raisonnement avec les théorèmes et les définitions adéquats. Entrainez-vous, lisez des démonstrations, c’est le meilleur moyen d’être par la suite capable d’en rédiger vous-même avec brio.
Étapes
Partie 1
Partie 1 sur 3:Comprendre le problème
-
1Identifiez la question. Votre première tâche consiste à déterminer ce que vous allez devoir prouver exactement. Cette question servira également de conclusion à la démonstration. Prenez le temps par la même occasion de repérer les hypothèses avec lesquelles vous allez travailler. C’est le point de départ de la compréhension du problème et de sa résolution.
-
2Faites des schémas. En mathématiques, quand on veut comprendre les tenants et les aboutissants d’un exercice, il est souvent utile de faire un schéma récapitulatif. C’est encore plus vrai en géométrie, où vous pourrez de cette façon visualiser directement ce que vous cherchez à prouver.
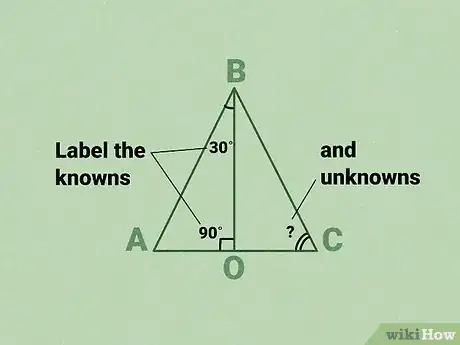
- Servez-vous de l’énoncé pour faire votre schéma. Listez les données connues et les inconnues.
- Notez au fur et à mesure toutes les informations qui pourront venir appuyer la démonstration.
-
3Étudiez. Apprendre à rédiger une preuve mathématique n’a rien d’une évidence. Pour vous aider, lisez et analysez des théorèmes apparentés à celui sur lequel vous travaillez pour tenter de comprendre comment ils sont construits.
- Dites-vous bien qu’une démonstration n’est en fait rien d’autre qu’une bonne argumentation dont les affirmations sont justifiées à chaque étape. Vous en trouverez de nombreux exemples dans vos manuels scolaires et sur internet qui pourront vous servir de modèles [1] .
-
4Posez des questions. Si vous avez des questions, n’hésitez pas à les poser à votre professeur ou à vos camarades de classe. Ces derniers s’interrogent peut-être également sur certaines parties du raisonnement, vous allez pouvoir travailler ensemble. Il vaut mieux demander de l’aide plutôt que de rester seul et de tâtonner à l’aveugle en espérant parvenir à un résultat.
- Allez parler à votre enseignant après le cours pour qu’il vous aiguille sur la bonne voie.
Publicité
Partie 2
Partie 2 sur 3:Inventer une démonstration
-
1Comprenez ce qu’est une démonstration. Il s’agit d’une série d’affirmations ordonnées de façon logique et étayées par des définitions et des théorèmes qui permet de prouver la véracité d’une autre affirmation [2] . C’est le seul et unique moyen de savoir si un raisonnement est juste d’un point de vue mathématique.
- Le fait d’être capable de rédiger des démonstrations atteste de façon indéniable de votre compréhension approfondie du problème et des concepts dont vous vous servez pour le résoudre.
- Cet exercice vous permet également de percevoir les mathématiques sous un jour nouveau très intéressant. Même dans les cas où vous ne parviendrez pas à terminer correctement vos démonstrations, le fait d’avoir essayé vous aidera à enrichir vos connaissances et à mieux comprendre votre cours.
-
2Tenez compte de votre public. Vous ne devez pas oublier pour quel type de lecteur vous travaillez et quel est son niveau de compréhension. On ne rédige pas de la même manière une démonstration destinée à être publiée dans une revue scientifique et un raisonnement dans le cadre d’un cours de maths de lycée [3] .
- Vous devez écrire en faisant en sorte que votre lecteur puisse suivre votre progression grâce au bagage de connaissances qu’il possède déjà.
-
3Identifiez le type de démonstration. Il y existe plusieurs modèles de démonstrations, vous en choisirez un en fonction des consignes qui vous ont été données et du lecteur auquel l’exercice est destiné. Si vous n’êtes pas certain de faire le bon choix, demandez l’aide de votre professeur. Au lycée, on ne s’attend pas toujours à ce que vous rédigiez une démonstration sous sa forme classique [4] .
- Une démonstration sous forme de tableau peut être faite en mettant dans la première colonne des affirmations et dans la seconde les arguments qui permettent de justifier ces affirmations. C’est souvent de cette manière que l’on procède en géométrie.
- Sous sa forme classique, la démonstration mathématique doit être rédigée avec des phrases grammaticalement correctes et sans aucun symbole. À un niveau universitaire, c’est ce qui sera exigé.
-
4Aidez-vous de la démonstration en deux colonnes. Mettre votre raisonnement sous forme de tableau vous permettra de connaitre les grandes lignes de votre démonstration avant de l’écrire sous forme classique. Vous pouvez vous appuyer sur le tableau pour organiser vos idées et réfléchir à la question. Tracez un trait à la verticale au milieu de votre feuille, puis inscrivez les données connues et toutes vos affirmations à gauche. Justifiez-les à droite à l’aide des définitions et théorèmes adéquats.
- Voici un exemple.
- Les angles A et B sont adjacents. Donné par l’énoncé.
- L’angle ABC est un angle plat. Définition de l’angle plat.
- L’angle ABC mesure 180°. Définition d’une droite.
- Angle A + Angle B = Angle ABC. Propriété de somme des angles.
- Angle A + Angle B = 180°. Remplacement par une valeur.
- Les angles A et B sont des angles supplémentaires. Définition des angles supplémentaires.
- C.Q.F.D.
-
5Passez du tableau au raisonnement standard. Appuyez-vous sur vos deux colonnes pour écrire la démonstration sous forme d’un paragraphe rédigé qui ne devra pas comporter trop de symboles ni d’abréviations.
- Par exemple : soient A et B des angles adjacents. Par hypothèse, les angles A et B sont supplémentaires. Comme ils sont supplémentaires et adjacents, les côtés des angles A et B forment une droite. La définition d’une ligne droite implique qu’elle délimite un angle à 180°. En nous appuyant sur les postulats concernant les sommes des angles, nous pouvons dire que l’addition des angles A et B nous donne la droite ABC. La somme des angles A et B est bien égale à 180°, par conséquent ce sont des angles supplémentaires. C.Q.F.D.
Publicité
Partie 3
Partie 3 sur 3:Rédiger une démonstration
-
1Familiarisez-vous avec le vocabulaire. Vous vous rendrez vite compte que certaines tournures de phrases reviennent sans arrêt dans les démonstrations. Vous devez apprendre à les connaitre et à les utiliser à bon escient pour réussir à écrire vous-même vos propres démonstrations [5] .
- Les formules de type « si A est vrai, alors B est vrai » signifient que vous devez prouver que chaque fois que A est vrai, B est également nécessairement vrai [6] .
- « A est vrai si et seulement si B est vrai » signifie que vous devez prouver que B et A sont vrais et faux en même temps. Montrez donc que « si A est vrai, alors B est vrai » et également que « si A est faux, alors B est faux ».
- « A n’est vrai que si B est vrai » est une autre formulation pour dire « si A est vrai, alors B est vrai ». C’est une tournure qui est moins courante, mais vous devez tout de même la connaitre au cas où vous la rencontriez.
- Lorsque vous rédigez votre démonstration, employez le « nous » plutôt que le « on [7] » .
-
2Répertoriez les données connues. Lorsque vous concevez une démonstration, votre première tâche consiste à identifier et lister toutes les informations fournies par l’énoncé. Cela vous permet de faire le point sur ce que vous savez et sur ce qui reste à établir pour parvenir à la preuve mathématique. Relisez attentivement votre problème et notez tout ce qui vous parait utile.
- Prenons un exemple : montrez que deux angles adjacents (A et B) sont supplémentaires.
- Ce qui est donné : les angles A et B sont adjacents.
- Ce qu’il faut prouver : les angles A et B sont supplémentaires.
-
3Définissez les variables. Une fois que vous avez sous les yeux toutes les données connues, il faut que vous donniez la définition de chaque variable. Pour que les choses soient claires pour votre lecteur, écrivez ces définitions en guise d’entrée en matière. Si vous ne le faites pas, il risque de très vite se perdre dans votre raisonnement.
- N’utilisez jamais de variables qui n’ont pas été préalablement définies.
- Dans notre exemple, les variables seront les mesures des angles A et B.
-
4Procédez à l’envers. Très souvent, il est bien plus facile de prendre le problème dans le sens inverse. Partez de la fin, c’est-à-dire de l’affirmation que vous tentez de démontrer et essayez de réfléchir à l’enchainement d’étapes logiques qui peuvent vous ramener au début du raisonnement.
- Travaillez sur les premières et les dernières étapes pour voir si vous pourriez les rendre similaires. Appuyez-vous pour cela sur les données connues, les définitions que vous avez apprises, ainsi que sur les démonstrations semblables auxquelles vous avez déjà été confronté.
- Interrogez-vous à toutes les étapes. « Pourquoi en est-il ainsi ? » et « Existe-t-il des cas dans lesquels ceci pourrait être faux ? » sont des questions très pertinentes à se poser tout au long de votre progression logique.
- N’oubliez pas de remettre toutes les étapes dans le bon ordre lors de la rédaction finale.
- Reprenons notre exemple : si A et B sont des angles supplémentaires, cela signifie que la somme de leurs mesures vaut 180°. La combinaison de ces deux angles forme la droite ABC. Vous savez qu’ils forment une droite grâce à la définition des angles adjacents. Étant donné qu’un segment de droite correspond aussi à un angle plat, la mesure est de 180°. Puisque l’angle issu de la droite fait 180°, vous pouvez procéder à une substitution pour montrer que si on les ajoute, les angles A et B font eux aussi 180°.
-
5Ordonnez vos étapes logiquement. Commencez par le début et progressez en direction de la conclusion. Même s’il est très pratique de réfléchir à l’envers quand on cherche la solution, au moment de rédiger la démonstration, il faut veiller à bien tout remettre dans le bon ordre, avec la conclusion à la fin [8] . Il faut que votre raisonnement se déroule étape par étape, avec une justification pour chaque affirmation, de telle sorte que le lecteur n’ait à aucun moment l’occasion de mettre en doute la validité de votre démonstration.
- Commencez avec les hypothèses sur lesquelles vous travaillez.
- Procédez avec des étapes simples et évidentes pour que le lecteur ne se demande jamais comment vous êtes passé d’une étape à une autre.
- N’hésitez surtout pas à faire plusieurs brouillons de votre démonstration. Faites autant d’essais que nécessaire pour réorganiser les étapes jusqu’à ce que vous parveniez à l’ordre le plus logique possible.
- En commençant par le début, cela donnera l'exemple ci-dessous.
- Les angles A et B sont adjacents.
- L’angle ABC est plat.
- L’angle ABC mesure 180°.
- Angle A + Angle B = Angle ABC.
- Angle A + Angle B = 180°.
- Les angles A et B sont donc supplémentaires.
-
6Évitez les flèches et abréviations. Au moment où vous faites le plan au brouillon, vous avez parfaitement le droit d’utiliser des symboles et de ne pas tout écrire en entier. En revanche, dans la mouture définitive, ces éléments risqueraient de nuire à la compréhension de votre lecteur, mieux vaut donc ne pas les employer et leur substituer des mots de liaison comme « donc » ou « par conséquent [9] ».
- La seule exception notable à cette règle est l’usage de l’acronyme C.Q.F.D (pour « ce qu’il fallait démontrer ») en fin d’exercice [10] .
-
7Justifiez. Toutes vos affirmations doivent être appuyées par des définitions, des théorèmes ou des lois mathématiques. C’est à cette condition seulement que votre démonstration sera valide. Aucun argument n’est valable s’il n’est pas accompagné d’une définition. Pour voir ce que cela peut donner concrètement, n’hésitez pas à vous reporter à des démonstrations proches de celle sur laquelle vous travaillez et qui vous serviront d’exemples.
- Testez votre démonstration en essayant de l’appliquer à un cas particulier pour lequel elle sera normalement fausse. Si elle n’est pas fausse alors que ce cas particulier est censé être exclu des conditions de la démonstration, vous devez revoir votre raisonnement.
- En géométrie, les démonstrations sont très souvent présentées sous forme de tableau à deux colonnes, avec une colonne pour l’argument et une pour la justification. Cependant, la forme habituelle de la démonstration classique est un paragraphe rédigé avec des phrases complètes.
-
8Concluez par C.Q.F.D. La dernière phrase de la démonstration doit être ce que vous essayiez de montrer. Une fois que vous l’avez écrite, terminez par l’acronyme C.Q.F.D ou bien faites un petit carré coloré pour signifier que votre travail est achevé [11] .
- On rencontre parfois la formule issue du latin Q.E.D. (quod erat demonstrandum), qui veut également dire « ce qu’il fallait démontrer ».
- Si vous n’êtes pas certain que votre démonstration soit convaincante, essayez d’écrire quelques phrases supplémentaires pour expliquer comment vous en êtes arrivé à cette conclusion et pourquoi cela fait sens à vos yeux.
Publicité
Conseils
- Tout ce que vous écrivez doit être en rapport avec ce que vous essayez de prouver au bout du compte. Si vous vous apercevez que vous avez écrit des choses qui n’ont rien à voir avec ce vers quoi vous tendez, vous pouvez parfaitement les supprimer.
Références
- ↑ http://www.proofwiki.org/wiki/Main_Page
- ↑ http://www.math.uconn.edu/~hurley/math315/proofgoldberger.pdf
- ↑ https://www.math.washington.edu/~lee/Writing/writing-proofs.pdf
- ↑ http://www.homeschoolmath.net/teaching/two-column-proof.php
- ↑ https://math.berkeley.edu/~hutching/teach/proofs.pdf
- ↑ http://www.math.ucsd.edu/~ebender/proofs.html
- ↑ http://www.ms.uky.edu/~kott/proof_help.pdf
- ↑ http://www.ms.uky.edu/~kott/proof_help.pdf
- ↑ http://www.ms.uky.edu/~kott/proof_help.pdf



































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 12 507 fois.