Comment mesurer un angle sans rapporteur

Coécrit par l'équipe de wikiHow

Le plus simple pour mesurer un angle est de recourir à un rapporteur. Mais comment faire si vous n'en avez pas à portée de main ? La mesure d'un angle peut s'effectuer en utilisant certaines propriétés de base des triangles. Pour les calculs, vous utiliserez une calculatrice (simple ou scientifique). Si vous n'avez pas de calculatrice, sur Internet, il y a tout ce qu'il faut en matière de calculatrices. Les calculs vont dépendre en fait du type d'angle auquel vous êtes confronté(e), selon qu'il est aigu (inférieur à 90°), obtus (compris entre 90° et 180°) ou encore rentrant (compris entre 180° et 360° ^{[1]
X
Source de recherche}).

Méthode 1

Méthode 1 sur 3:
Mesurer un angle aigu

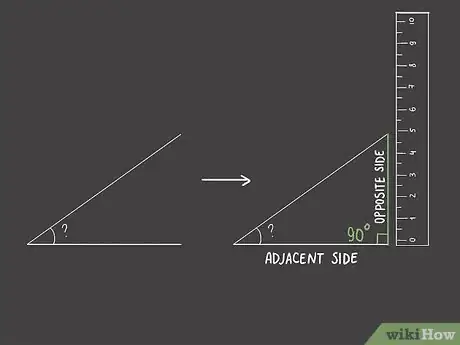
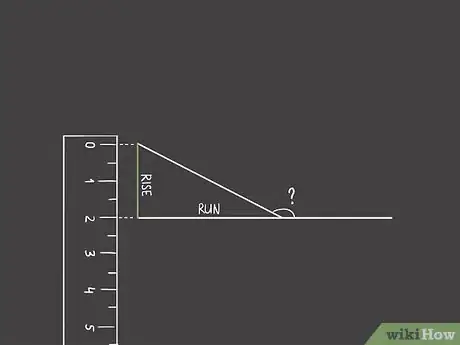
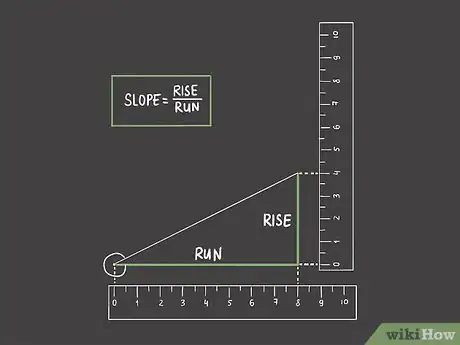
1
Tracez un trait vertical fermant votre angle aigu. Pour obtenir la mesure en degrés d'un angle aigu, vous devez relier les deux segments de votre angle en sorte de former un triangle rectangle. Si l'un des segments est horizontal, partez de l'extrémité de l'autre segment et tracez verticalement vers le bas une ligne qui va venir couper à angle droit le premier segment, comme sur l'illustration ^{[2]
X
Source de recherche}.
- L'angle à l'intersection est droit, c'est-à-dire que sa mesure est de 90°. La ligne verticale est le côté opposé à votre angle aigu et le segment horizontal est le côté adjacent de ce même angle.
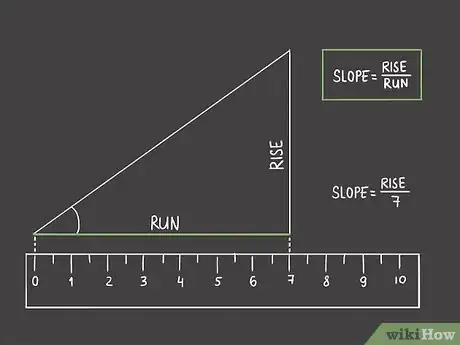
2
Mesurez la longueur du côté adjacent à l'angle aigu. Ce sera la distance. Mesurez-la en partant de la gauche, donc du sommet de l'angle le long du segment horizontal jusqu'à l'angle droit formé par votre triangle, c'est-à-dire jusqu'au point d'intersection avec le segment vertical ^{[3]
X
Source de recherche}.
- La pente ( $p$ ) du segment oblique (hypoténuse du triangle rectangle) est donnée par la formule : $p={\frac {{\acute {e}}l{\acute {e}}vation}{distance}}$ . Ainsi, si vous mesurez une distance horizontale de 7 cm, la formule devient : $p={\frac {{\acute {e}}l{\acute {e}}vation}{7}}$ .
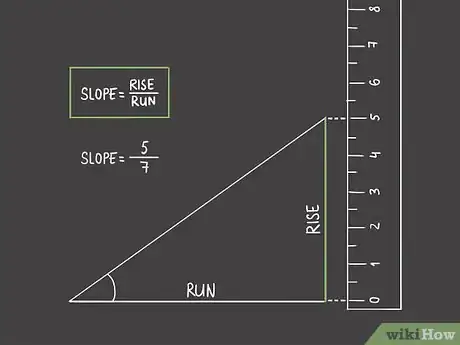
3
Mesurez la longueur du côté opposé à l'angle aigu. Ce sera l'élévation et elle est matérialisée par le trait vertical. Mesurez ce dernier de l'extrémité du segment non horizontal (en fait, l'hypoténuse de votre triangle rectangle) jusqu'au point d'intersection avec le segment vertical ^{[4]
X
Source de recherche}.
- Ce que vous venez de mesurer est l'élévation que l'on retrouve en numérateur dans la formule de la pente. Si vous trouvez une élévation de 5 cm, après regroupement avec la mesure précédente, la formule devient : $p={\frac {5}{7}}$ .
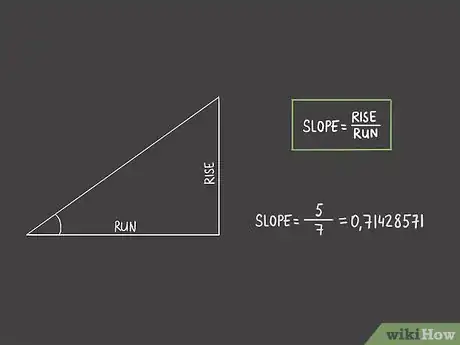
4
Calculez la pente. C'est simple : divisez l'élévation par la distance. Cette pente est en fait l'inclinaison de la ligne diagonale, l'hypoténuse de votre triangle. Le résultat de cette division est nécessaire pour calculer en degrés la valeur de l'angle aigu ^{[5]
X
Source de recherche}.
- Passez au calcul de la pente : vous devez donc diviser 5 par 7, ce qui donne un résultat de 0,71428571.
Conseil : n'arrondissez pas tout de suite le résultat, vous auriez une mauvaise mesure de votre angle.
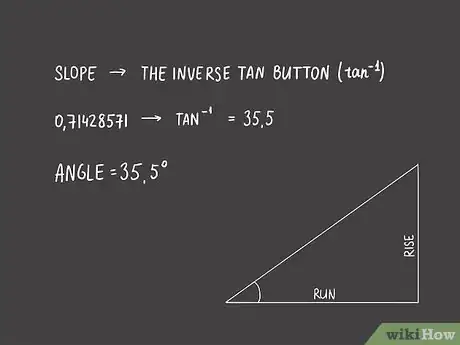
5
Servez-vous d'une calculatrice scientifique. Le calcul de l'angle nécessite l'utilisation de la fonction inverse de la tangente qui est la fonction arc tangente
( $arctan$ $arctan$ ), d'où l'intérêt de cette calculatrice. Sur votre machine, appuyez sur la touche d'inversion jaune 2nd, puis sur la touche tan. Tapez la valeur de la pente, puis validez : vous voyez s'afficher en degrés la valeur de votre angle ^{[6]
X
Source de recherche}.
- Si vous faites le calcul avec votre pente de 0,71428571, vous trouvez un angle d'un peu plus de 35,5°.
Publicité

Méthode 2

Méthode 2 sur 3:
Mesurer un angle obtus

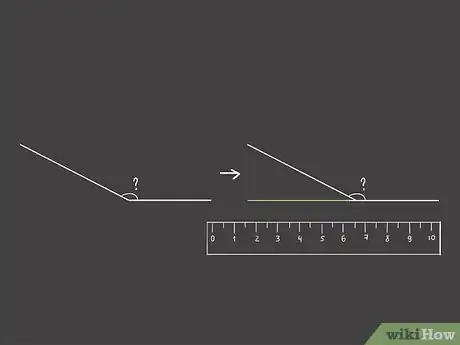
1
Prolongez le segment horizontal. Tracez à la règle sous le segment oblique un trait bien horizontal dans le prolongement du segment déjà tracé. Ce trait doit être prolongé au minimum jusqu'au point qui est à l'aplomb de l'extrémité du segment oblique ^{[7]
X
Source de recherche}.
- Ce trait que vous tracez doit être parfaitement horizontal et dans le prolongement, sans quoi vos calculs seront faux.
Conseil : si vous voulez un trait parfaitement horizontal, servez-vous du bord de la page que vous alignerez avec le petit côté de votre règle, comme une équerre.
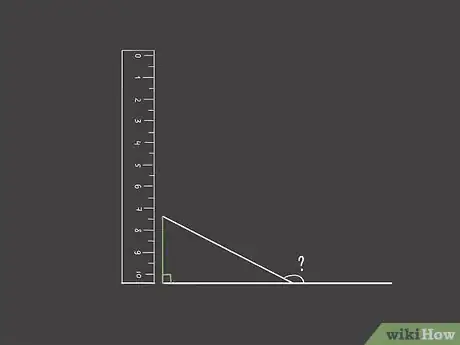
2
Tracez un trait vertical qui part vers le bas depuis le segment oblique. Alignez le petit côté de votre règle sur le trait horizontal et faites-la glisser ainsi jusqu'au bout du segment oblique. Tracez un trait vertical qui est à angle droit avec l'horizontale ^{[8]
X
Source de recherche}.
- Vous obtenez donc un triangle rectangle dont l'angle droit est sur la même ligne horizontale que l'angle recherché, mais décalé sur la gauche. L'hypoténuse de ce triangle rectangle est le segment oblique de l'angle à trouver.
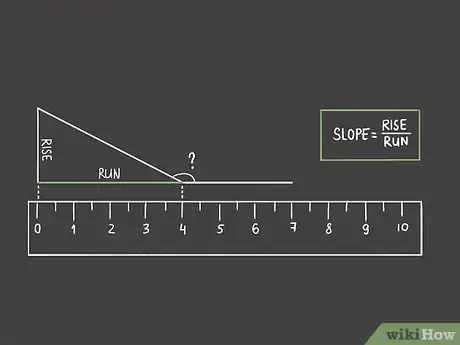
3
Mesurez la longueur du segment prolongé. Avec le plus de précision possible, mesurez avec un double décimètre le segment que vous avez rajouté. La mesure se fera à l'horizontale depuis l'angle droit, point d'intersection avec le trait vertical, jusqu'au point qui marque le sommet de votre angle ^{[9]
X
Source de recherche}.
- L'objectif, comme dans la méthode précédente, est de calculer la pente du segment oblique afin de calculer l'angle aigu, lequel servira ensuite au calcul de l'angle obtus : ces deux angles ensemble sont dits supplémentaires, car la somme de leurs angles est de 180°. Comme plus haut, la formule de la pente est : $p={\frac {{\acute {e}}l{\acute {e}}vation}{distance}}$ .
4
Mesurez la longueur du trait vertical. Placez correctement votre règle et lisez la mesure du trait vertical du haut jusqu'en bas. Appliquez-vous pour cette mesure : plus vous serez précis(e), éventuellement au demi-millimètre, plus fin sera votre résultat ^{[10]
X
Source de recherche}.
- La longueur de votre trait vertical représente l'élévation dans la formule de la pente (p) : $p={\frac {{\acute {e}}l{\acute {e}}vation}{distance}}$ . Maintenant, vous avez toutes les données pour calculer la pente du segment oblique.
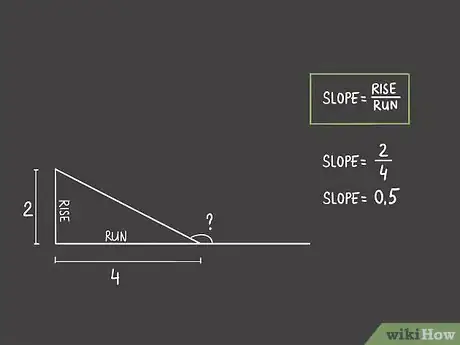
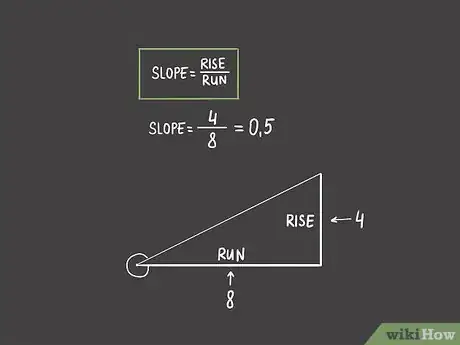
5
Calculez la pente de votre angle aigu. C'est toujours aussi simple : divisez l'élévation par la distance. Comme les unités s'annulent, vous vous retrouvez avec une valeur sans unité : la pente ^{[11]
X
Source de recherche}.
- Supposons que vous ayez une élévation de 2 m tous les 4 m, la pente serait de :
  $p={\frac {2}{4}}=0,5$ .
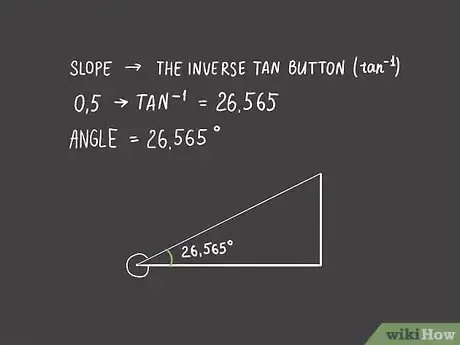
6
Calculez la mesure de l'angle aigu. Sur une calculatrice scientifique, appuyez sur la touche d'inversion jaune 2nd, puis sur la touche tan. Tapez la valeur de la pente, puis validez : vous voyez s'afficher en degrés la valeur de votre angle ^{[12]
X
Source de recherche}.
- Si vous faites le calcul avec votre pente de 0,5, vous devriez trouver un angle de 26,565°.
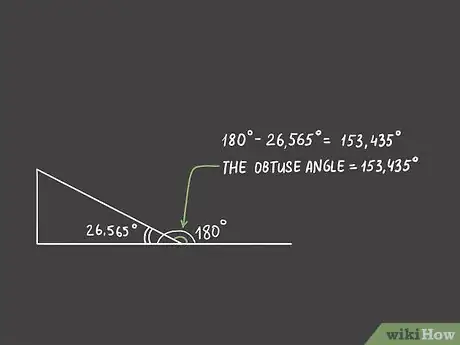
7
Calculez la mesure de l'angle obtus. C'était bien cette mesure qu'il nous fallait. Un angle plat (demi-cercle) mesure 180° et peut se décomposer en la somme de deux angles, l'un aigu, l'autre obtus. En prolongeant votre segment, vous avez créé un angle plat, puis calculé un angle aigu : son supplémentaire (angle qui, ajouté à l'angle de référence, mesure 180°), l'obtus, a une mesure équivalant à : 180° - angle aigu ^{[13]
X
Source de recherche}.
- Nous avons trouvé un angle aigu de 26,565°, l'angle obtus supplémentaire mesure : 153,435° (180 – 26,565 = 153,435). Vous pouvez éventuellement arrondir à 153,4°, voire 153°.
Publicité

Méthode 3

Méthode 3 sur 3:
Mesurer un angle rentrant

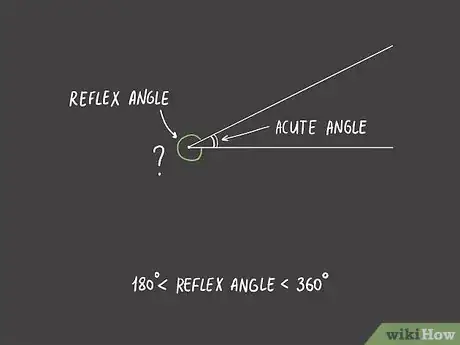
1
Portez une attention particulière à l'angle saillant correspondant. Un angle rentrant a une mesure comprise entre 180° et 360°. Si vous regardez l'illustration, vous voyez que cet angle est associé, en complément en quelque sorte même si le terme n'est pas approprié, à un angle aigu (dit « saillant») pour former un angle de 360° ^{[14]
X
Source de recherche}.
- Si vous parvenez à déterminer la mesure de l'angle saillant correspondant, il vous suffira d'une soustraction pour connaitre la mesure de l'angle rentrant. Cet angle saillant correspondant est un angle soit aigu soit obtus, dans les deux cas, vous utiliserez la formule de la pente, puis la fonction arc tangente.
Conseil : au besoin, vous pouvez tourner votre figure pour plus de lisibilité. Quant à l'angle rentrant, n'en tenez pas compte pour l'instant.
2
Tracez un triangle rectangle. Reliez à la règle les extrémités des deux segments de l'angle aigu en sorte de former un triangle rectangle. Si l'un des segments est horizontal, partez de l'extrémité de l'autre segment et tracez verticalement vers le bas une ligne qui va venir couper à angle droit le premier segment, comme sur l'illustration ^{[15]
X
Source de recherche}.
- Le segment horizontal est le côté adjacent au petit angle du triangle, et le trait vertical le côté opposé au même angle aigu, le segment oblique est l'hypoténuse.
3
Mesurez l'élévation et la distance de l'angle aigu. La formule qui va nous servir au calcul de l'angle est celle de la pente (p) : $p={\frac {{\acute {e}}l{\acute {e}}vation}{distance}}$ $p={\frac {{\acute {e}}l{\acute {e}}vation}{distance}}$ , l'élévation est la longueur du trait vertical, soit le côté opposé à l'angle. La distance est la longueur du segment horizontal, soit le côté adjacent au même angle ^{[16]
X
Source de recherche}.
- Mesurez la longueur du côté adjacent à l'angle aigu (segment horizontal), puis celle du côté opposé (trait vertical), l'ordre n'a pas vraiment d'importance, le tout étant d'avoir les deux mesures pour pouvoir faire le calcul.
4
Calculez la pente de votre angle aigu. C'est toujours aussi simple : divisez l'élévation par la distance. Reprenez la formule de la pente, remplacez l'élévation et la distance par les valeurs trouvées, puis faites les calculs et vous aurez votre pente, laquelle n'a pas d'unité, car les unités s'annulent ^{[17]
X
Source de recherche}.
- Supposons que vous ayez une élévation de 4 cm tous les 8 cm, comme indiqué sur l'illustration, la pente serait de : $p={\frac {4}{8}}=0,5$ , la même que précédemment.
5
Utilisez votre calculatrice pour trouver l'angle aigu. Sur une calculatrice scientifique, appuyez sur la touche d'inversion jaune 2nd, puis sur la touche tan. Tapez la valeur de la pente, puis validez : vous voyez s'afficher en degrés la valeur de votre angle ^{[18]
X
Source de recherche}.
- Si vous faites le calcul avec votre pente de 0,5, vous devriez trouver un angle de 26,565°.
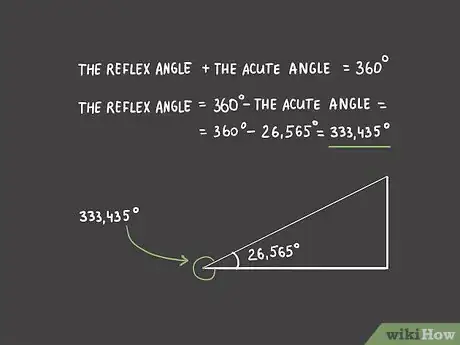
6
Trouvez la mesure de l'angle rentrant. C’est très simple, puisqu'il s'agit de faire une simple soustraction, celle du complément de l'angle trouvé à 360°, cette dernière valeur étant la mesure d'un cercle complet. Si l'angle saillant correspondant était obtus, vous procèderiez ici exactement de la même façon ^{[19]
X
Source de recherche}.
- Dans notre exemple, nous avons un angle saillant correspondant (aigu) de 26,565 degrés : votre angle rentrant mesure donc 333,435° (360 - 26,565). Vous pouvez éventuellement arrondir à 333,4°, voire 333°.
Publicité

Conseils

Faites très attention à bien régler votre calculatrice sur les degrés, et non les radians, sans quoi vos résultats seront faux. Consultez la notice de votre calculatrice pour le changement d'unité.
La pente est proportionnelle à l'élévation et inversement proportionnelle à la distance. Concernant les unités de ces deux unités de longueur, prenez celle que vous voulez, mais elle doit être identique : vous mesurez l'élévation en centimètres, la distance sera en centimètres. Quant à la pente, elle n'a pas d'unité.