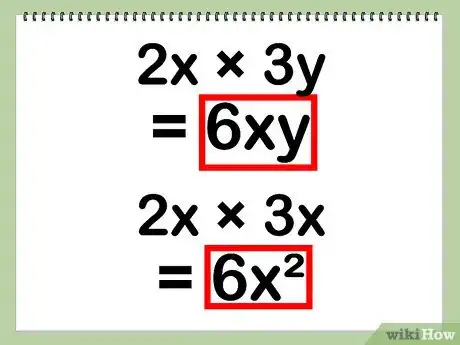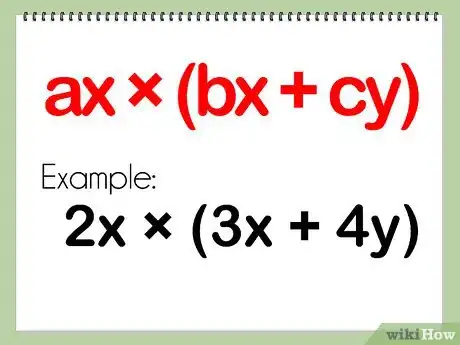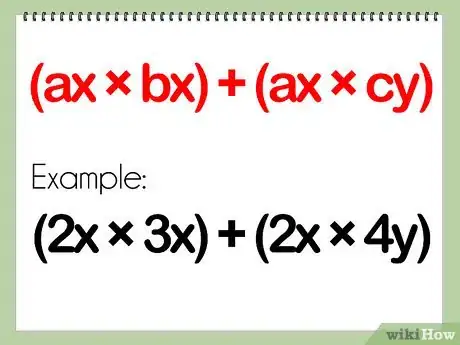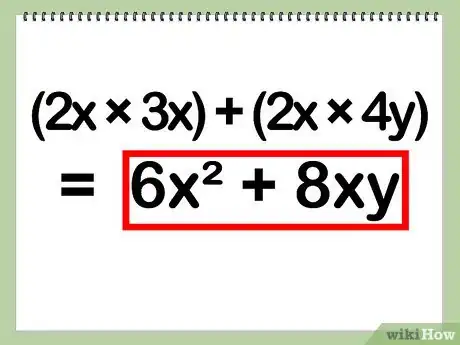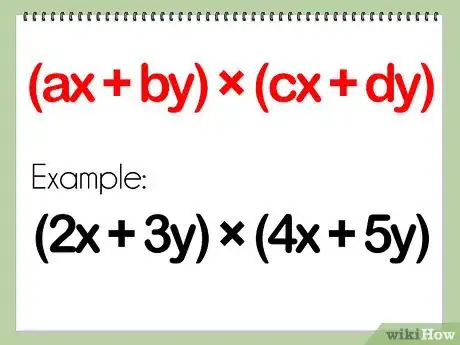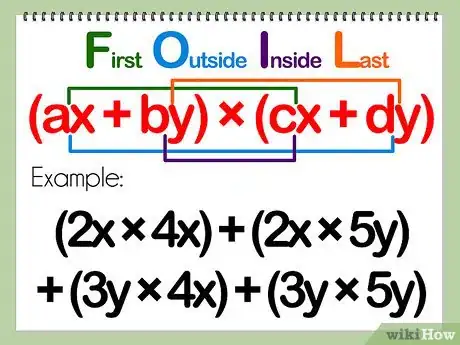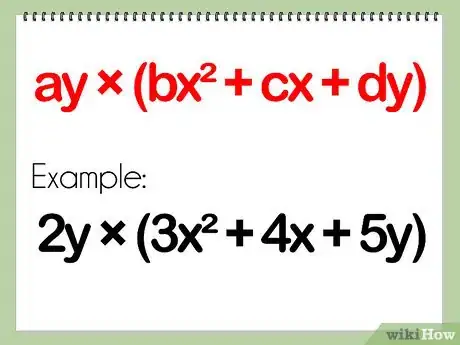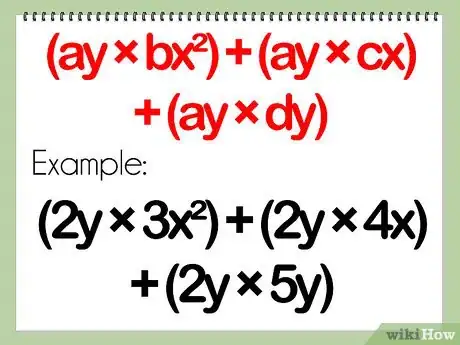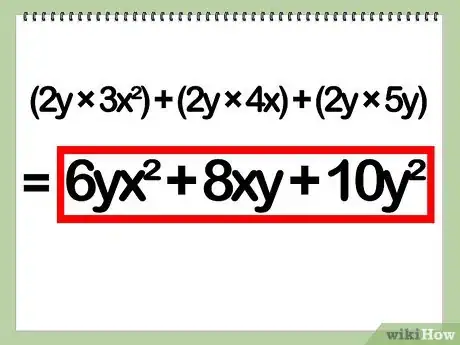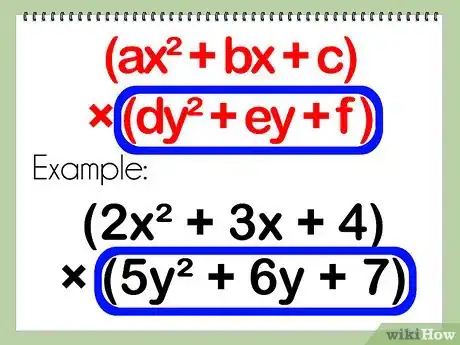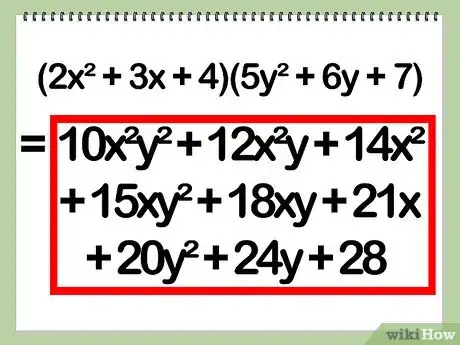Comment multiplier des polynômes

Informations concernant l'auteur.e

Les polynômes sont des expressions mathématiques composées de termes qui comprennent des variables (ou inconnues) affectées de coefficients numériques. Ces polynômes se présentent sous différentes formes et il y a donc des règles à respecter pour les multiplier entre eux.

Méthode 1

Méthode 1 sur 5:
Multiplier deux monômes

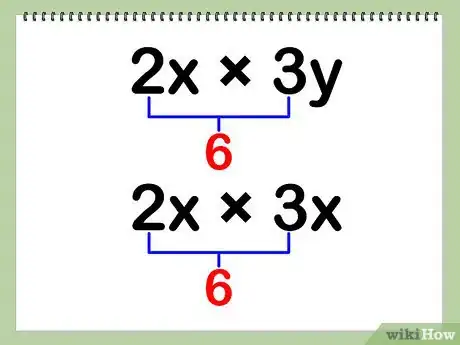
1
Examinons de plus près le problème. Un problème avec deux monômes ne met en jeu qu’une multiplication. Il n’y a ni soustraction ni addition.
- Un problème de polynômes impliquant deux monômes (polynôme à un seul terme) se présente sous cette forme : (ax) x (by) ou (ax) x (bx).
- Exemple : (2x) x (3y)
- Exemple : (2x) x (3x)
  - Nota bene : a et b sont des constantes (nombres ou chiffres), tandis que x et y sont des variables (ou inconnues)
2
Multipliez les coefficients. Les coefficients sont les valeurs numériques. Ils se multiplient entre eux selon les règles des tables de multiplication.
- Durant votre exercice, vous allez devoir multiplier tout simplement a et b.
- Exemple : (2x) x (3y) = (6)(x)(y)
- Exemple : (2x) x (3x) = (6)(x)(x)
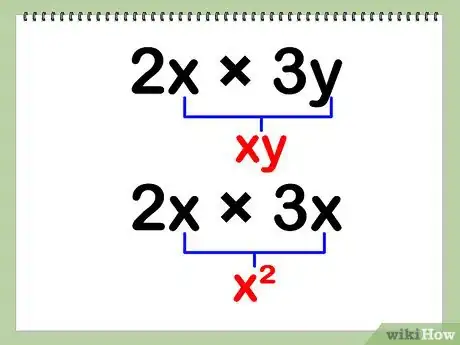
3
Multipliez les variables. Les variables se présentent sous la forme de lettres dans l’équation. Quand vous les multipliez entre elles, elles se juxtaposent si elles sont différentes, mais elles sont élevées au carré si elles sont identiques.
- Nota bene : quand vous multipliez une variable par elle-même, vous élevez cette variable à une puissance supérieure.
- En d’autres termes, vous multipliez le x et le y ou le x et le x ensemble.
- Exemple : 2x x 3y = (6)(x)(y) = 6xy
- Exemple : 2x x 3x = (6)(x)(x) = 6x²
4
Inscrivez votre réponse finale. Le problème étant simple au départ, il n’y a plus rien à faire.
- Le produit (ax) x (by) donne abxy. De la même façon, le produit (ax) x (bx) donne abx².
- Exemple : 6xy
- Exemple : 6x²
Publicité

Méthode 2

Méthode 2 sur 5:
Multiplier un monôme et un binôme

1
Examinons de plus près le problème. Dans ce cas de figure, on a deux polynômes, l’un composé d’un seul terme, le monôme et l’autre, composé de 2 termes, séparés par un signe « + » ou un signe « - » : c’est le binôme.
- Le produit d’un monôme et d’un binôme ressemble à quelque chose comme : (ax) x (bx + cy)
- Exemple : (2x)(3x + 4y)
2
Multipliez chacun des deux termes du binôme par le monôme. On dit aussi développer le produit. Reformulez alors le produit qui devient une somme de produits.
- Si on reprend notre exemple, le produit d’origine devient : (ax x bx) + (ax x cy)
- Exemple : (2x)(3x + 4y) = (2x)(3x) + (2x)(4y)
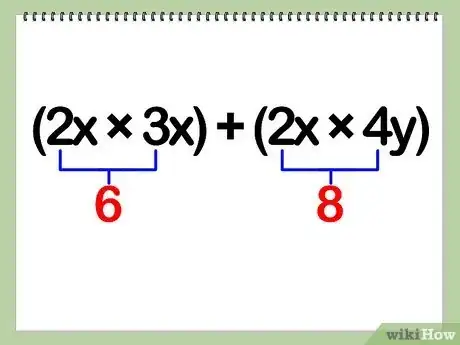
3
Multipliez les coefficients. Les coefficients sont les valeurs numériques. Ils se multiplient entre eux selon les règles des tables de multiplication.
- Durant votre exercice, vous allez devoir multiplier tout simplement a, b et c ensemble.
- Exemple : (2x)(3x + 4y) = (2x)(3x) + (2x)(4y) = 6(x)(x) + 8(x)(y)
4
Multipliez les variables. Les variables se présentent sous la forme de lettres dans l’équation. Quand vous les multipliez entre elles, elles se juxtaposent si elles sont différentes, mais elles sont élevées au carré si elles sont identiques.
- En d’autres termes, vous devez multiplier les x et les y de l’équation.
- Exemple : (2x)(3x + 4y) = (2x)(3x) + (2x)(4y) = 6(x)(x) + 8(x)(y) = 6x² + 8xy
5
Inscrivez votre réponse définitive. Le problème étant simple au départ, il n’y a plus rien à faire.
- Vous obtenez quelque chose comme : abx² + acxy
- Exemple : 6x² + 8xy
Publicité

Méthode 3

Méthode 3 sur 5:
Multiplier deux binômes

1
Examinons de plus près le problème. Dans ce cas de figure, on a deux polynômes, composés tous deux de 2 termes (binômes), séparés par un signe « + » ou un signe « - ».
- Un problème de polynômes impliquant deux binômes se présente sous cette forme : (ax + by) x (cx + dy)
- Exemple : (2x + 3y)(4x + 5y)
2
Retenez le terme mnémotechnique de PEID pour développer correctement. PEID est un acronyme qui s’explique de la façon suivante : Premiers termes, puis les termes Extérieurs, puis les termes Intérieurs et enfin, les Derniers termes.
- Après cette manipulation, l’expression devient quelque chose comme : (ax)(cx) + (ax)(dy) + (by)(cx) + (by)(dy)
- Exemple : (2x + 3y)(4x + 5y) = (2x)(4x) + (2x)(5y) + (3y)(4x) + (3y)(5y)
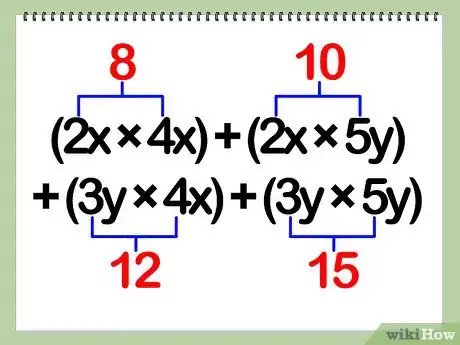
3
Multipliez les coefficients. Les coefficients sont les valeurs numériques. Ils se multiplient entre eux selon les règles des tables de multiplication.
- Durant votre exercice, vous allez devoir multiplier tout simplement a, b, c et d ensemble.
- Exemple : (2x)(4x) + (2x)(5y) + (3y)(4x) + (3y)(5y) = 8(x)(x) + 10(x)(y) + 12(y)(x) + 15(y)(y)
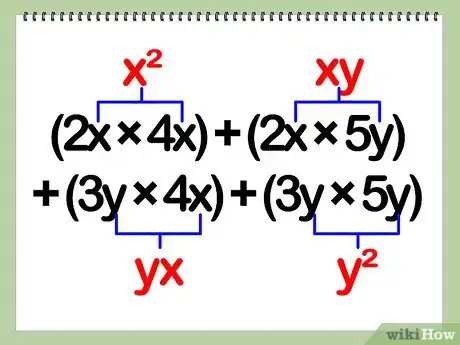
4
Multipliez les variables. Les variables se présentent sous la forme de lettres dans l’équation. Quand vous les multipliez entre elles, elles se juxtaposent si elles sont différentes, mais elles sont élevées au carré si elles sont identiques.
- En d’autres termes, vous devez multiplier les x et les y de l’équation.
- Exemple : 8(x)(x) + 10(x)(y) + 12(y)(x) + 15(y)(y) = 8x² + 10xy + 12xy + 15y²
5
Il faut ensuite additionner les termes identiques, s’il y en a, pour pouvoir donner la réponse finale. Dans ce cas, les expressions multipliées sont assez longues pour donner des termes identiques (des « xy », par exemple). Il suffit dès lors de les additionner ou de les soustraire pour obtenir la réponse définitive et simplifiée.
- Après cette manipulation, l’expression devient quelque chose comme : acx² + adxy + bcxy + bdy² = acx² + abcdxy + bdy²
- Exemple : 8x² + 22xy + 15y²
Publicité

Méthode 4

Méthode 4 sur 5:
Multiplier un monôme et un trinôme

1
Examinons de plus près le problème. Dans ce cas de figure, on a deux polynômes, l’un composé d’un seul terme, le monôme et l’autre, composé de 3 termes, séparés par un signe « + » ou un signe « - » : c’est le trinôme.
- Un problème de polynômes impliquant un monôme et un trinôme se présente sous cette forme : (ay) x (bx² + cx + dy)
- Exemple : (2y)(3x² + 4x + 5y)
2
Multipliez chacun des trois termes du trinôme par le monôme. On dit aussi développer le produit. Reformulez alors le produit qui devient une somme de produits.
- Si on reprend notre exemple, le produit d’origine devient : (ay)(bx²) + (ay)(cx) + (ay)(dy)
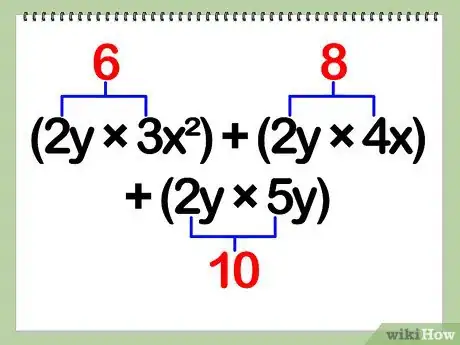
- Exemple : (2y)(3x² + 4x + 5y) = (2y)(3x²) + (2y)(4x) + (2y)(5y)
3
Multipliez les coefficients. Les coefficients sont les valeurs numériques. Ils se multiplient entre eux selon les règles des tables de multiplication.
- Durant votre exercice, vous allez devoir multiplier tout simplement a, b, c et d ensemble.
- Exemple : (2y)(3x²) + (2y)(4x) + (2y)(5y) = 6(y)(x²) + 8(y)(x) + 10(y)(y)
4
Multipliez les variables. Les variables se présentent sous la forme de lettres dans l’équation. Quand vous les multipliez entre elles, elles se juxtaposent si elles sont différentes, mais elles sont élevées au carré si elles sont identiques.
- Vous devez multiplier les x et les y de l’équation.
- Exemple : 6(y)(x²) + 8(y)(x) + 10(y)(y) = 6yx² + 8xy + 10y²
5
Inscrivez votre réponse définitive. Le problème étant simple au départ, il n’y a plus rien à faire.
- Une fois tout calculé, la réponse finale se présente sous une forme du genre : abyx² + acxy + ady².
- Avec des valeurs réelles comme coefficients, on obtient : 6yx² + 8xy + 10y²
Publicité

Méthode 5

Méthode 5 sur 5:
Multiplier deux polynômes

1
Examinons de plus près le problème. Chaque polynôme est composé de trois termes (ou plus) séparés chacun d’un signe « + » ou d’un signe « - ».
- Un problème de polynômes impliquant deux trinômes se présente sous cette forme : (ax² + bx + c) x (dy² + ey + f)
- Exemple : (2x² + 3x + 4)(5y² + 6y + 7)
- Nota bene : ce qui marche pour des trinômes marche aussi pour les polynômes à 4 , 5 , 6… termes !
2
Traitez le second polynôme comme un seul terme ^{[1]
X
Source de recherche}. Le second polynôme reste inchangé.
- Le second polynôme correspond ici à (dy^ 2 + ey + f).
- Exemple : (5y² + 6y + 7)
3
Multipliez chacun des termes du premier polynôme par le second polynôme. Pour l’instant, on considère le second polynôme comme un tout et on le multiplie donc à chacun des trois termes du premier polynôme.
- Après cette manipulation, l’expression devient quelque chose comme : (ax²)(dy² + ey + f) + (bx)(dy² + ey + f) + (c)(dy² + ey + f)
- Exemple : (2x²)(5y² + 6y + 7) + (3x)(5y² + 6y + 7) + (4)(5y² + 6y + 7)
4
Développez chacun des trois éléments de l’expression. On prend le premier terme du premier polynôme et on le multiplie à l’ensemble des termes du second. On fait ensuite la même chose avec le second terme du premier polynôme. Idem avec le troisième terme.
- Après ces calculs, l’expression devient quelque chose comme : (ax²)(dy²) + (ax²)(ey) + (ax²)(f) + (bx)(dy²) + (bx)(ey) + (bx)(f) + (c)(dy²) + (c)(ey) + (c)(f)
- Exemple : (2x²)(5y²) + (2x²)(6y) + (2x²)(7) + (3x)(5y²) + (3x)(6y) + (3x)(7) + (4)(5y²) + (4)(6y) + (4)(7)
5
Multipliez chacun des coefficients. Les coefficients sont les valeurs numériques. Ils se multiplient entre eux selon les règles des tables de multiplication.
- Durant votre exercice, vous allez devoir multiplier tout simplement a, b, c, d, e et f ensemble.
- Exemple : 10(x²)(y²) + 12(x²)(y) + 14(x²) + 15(x)(y²) + 18(x)(y) + 21(x) + 20(y²) + 24(y) + 28
6
Multipliez chacune des variables. Les variables se présentent sous la forme de lettres dans l’équation. Quand vous les multipliez entre elles, elles se juxtaposent si elles sont différentes, mais elles sont élevées au carré si elles sont identiques.
- En d’autres termes, vous devez multiplier les x et les y de l’équation.
- Exemple : 10x²)² + 12x²) + 14x² + 15xy² + 18xy + 21x + 20y² + 24y + 28
7
Il faut ensuite additionner les termes identiques, s’il y en a, pour pouvoir donner la réponse finale. Dans ce cas, les expressions multipliées sont assez longues pour donner des termes identiques (des « xy », par exemple). Il suffit dès lors de les additionner ou de les soustraire pour obtenir la réponse définitive et simplifiée.
- Exemple : 10x²)² + 12x²) + 14x² + 15xy² + 18xy + 21x + 20y² + 24y + 28
Publicité