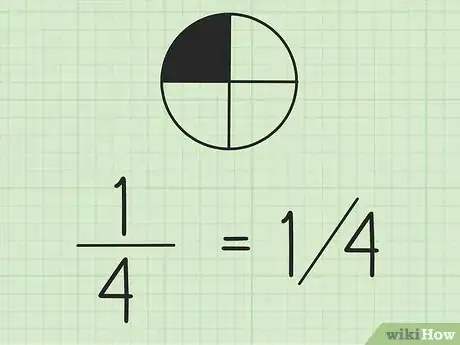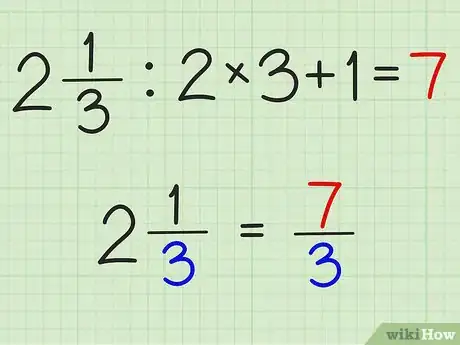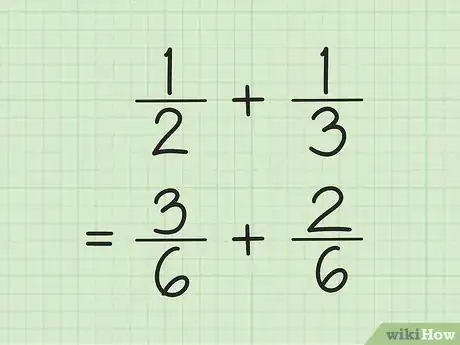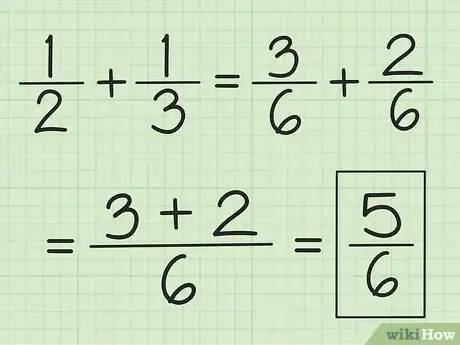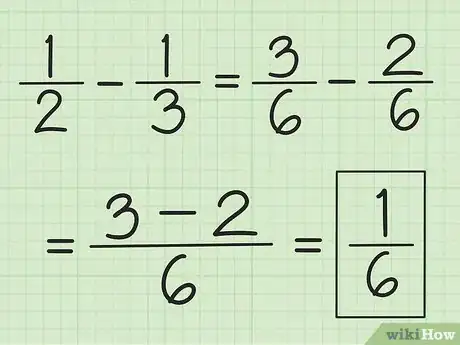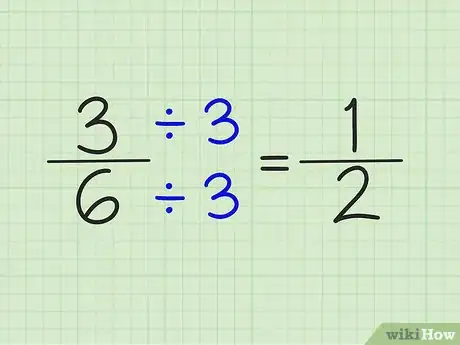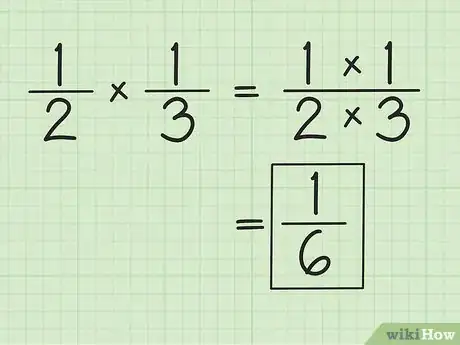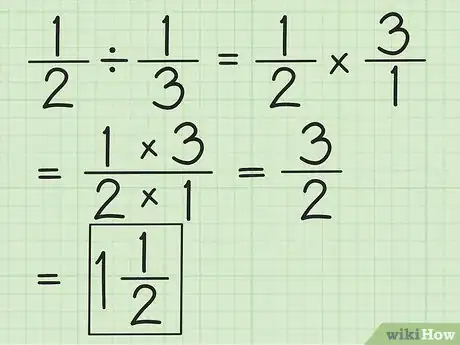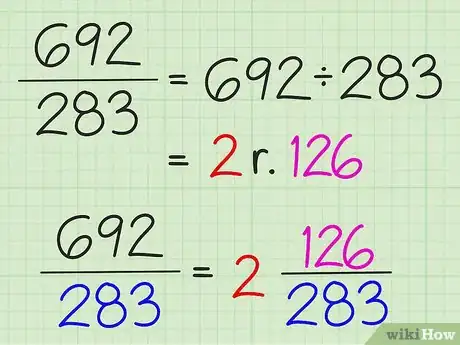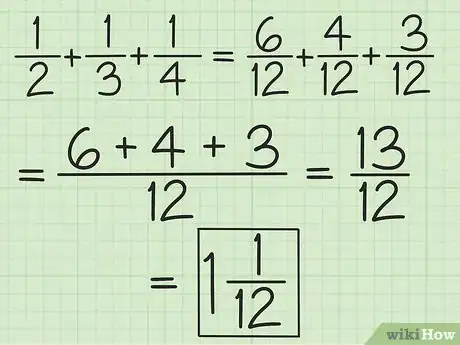Comment opérer avec des fractions

Informations concernant l'auteur.e

Pour certains élèves, quand vient l'étude des fractions, l'angoisse monte. C'est une branche de l'algèbre qui peut sembler, au premier abord, un peu difficile en soi, ne serait-ce que par les formes particulières des fractions. Ce monde des fractions possède ses propres règles (relativement simples) grâce auxquelles vous allez pouvoir les additionner, les soustraire, les multiplier ou encore les diviser, mais une fois ces règles retenues, c'est de l'algèbre assez simple. Une fois de plus, tout est question de pratique !

Méthode 1

Méthode 1 sur 5:
Comprendre ce qu'est une fraction

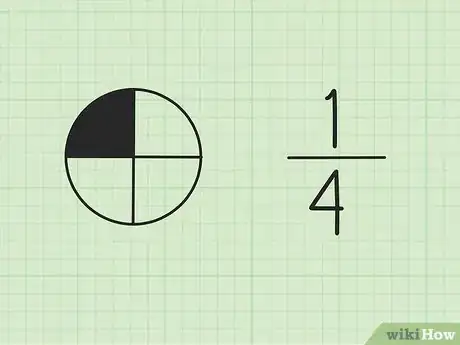
1
Sachez qu'une fraction représente la part d'un tout. La valeur du bas (aussi appelée « dénominateur ») représente le nombre de parts d'un tout, tandis que la valeur du haut (le « numérateur ») représente un certain nombre de parts du tout.
2
Sachez qu'une fraction peut s'écrire sous la forme a/b. La valeur de gauche est le numérateur, celle de droite, le dénominateur. Si vous êtes mal à l'aise avec cette écriture, rien ne vous empêche d'écrire la fraction avec le numérateur en haut, et le dénominateur en bas.
- Admettons que vous ayez acheté une pizza et que vous la coupiez en 4. Si vous prenez une part, elle représente 1/4 de la pizza. Si dans un exercice, sont évoqués les 7/3 pizzas, cela signifie qu'il y a 2 pizzas complètes, plus un tiers d'une troisième pizza, identique aux autres.
Publicité

Méthode 2

Méthode 2 sur 5:
Opérer avec des fractions et des nombres fractionnaires

1
Sachez ce qu'est un nombre fractionnaire. C'est une expression numérique formée d'un nombre naturel (« partie entière ») et d'une fraction inférieure à 1 (« partie fractionnaire »). 2 1/3 et 45 1/2 sont des nombres fractionnaires. Tout nombre fractionnaire peut s'écrire sous la forme d'une simple fraction, plus facile à manipuler.
2
Transformez un nombre fractionnaire en fraction. Pour cela, multipliez la partie entière par le dénominateur de la partie fractionnaire. Rapportez ce résultat sur le dénominateur, additionnez les deux numérateurs sans toucher au dénominateur. Vous avez une fraction dite « impropre ».
- Ainsi, 2 1/3 devient : (2 x3)/3 + 1/3 = 6/3 + 1/3, soit 7/3.
3
Transformez une fraction en un nombre fractionnaire. Divisez le numérateur par le dénominateur. Le résultat obtenu (quotient) est la partie entière et le reste de la division sur le dénominateur devient la partie fractionnaire.
- Ainsi, pour transformer 7/3 en nombre fractionnaire, divisez 7 par 3, ce qui vous donne 2 et il reste 1 (7 = (3 x 2) + 1). En conséquence, 7/3 = 2 1/3. Cette transformation n'est possible que si le numérateur est supérieur au dénominateur.
Publicité

Méthode 3

Méthode 3 sur 5:
Additionner et soustraire des fractions

1
Calculez le dénominateur commun des fractions. C'est obligatoire pour additionner ou soustraire. Le plus souvent, il suffit de multiplier les deux dénominateurs pour obtenir le dénominateur commun. Ce faisant, vous devez multiplier chaque numérateur par le dénominateur de l'autre fraction. Il arrive aussi qu'on trouve un dénominateur commun plus petit.
- Additionnez, par exemple, 1/2 et 1/3. Les dénominateurs étant différents, il faut les ramener au même dénominateur. Multipliez-les, ce qui vous donne 6 (2 x 3). Multipliez ensuite le 1 de 1/2 par 3, et le 1 de 1/3 par 2. Vous obtenez deux fractions avec le même dénominateur : 3/6 et 2/6.
- En regardant de plus près la première fraction, vous voyez que 3 est la moitié (1/2) de 6, et pour la seconde fraction, vous notez que 2 est le tiers (1/3) de 6. En conséquence, 1/3 et 2/6 ont la même valeur. Par contre, les fractions 1/3 et 1/6 ont un dénominateur commun de 18, mais il en existe un plus petit, à savoir 6, car 6 = 2 x 3.
2
Additionnez les numérateurs. Dans le même temps, vous devez conserver le même dénominateur.
- Si vous additionnez 3/6 et 2/6, vous obtenez 5/6, et en additionnant 2/6 et 1/6, vous obtenez 3/6.
3
Utilisez la même technique pour la soustraction. Trouvez dans un premier temps, le plus petit commun dénominateur (PPCD), rectifiez les numérateurs et soustrayez-les dans le bon sens. Donnez le résultat sur le dénominateur commun.
- Pour soustraire 1/3 de 1/2, vous devez tout ramener sur 6, ce qui donne respectivement 2/6 et 3/6. Vous ôtez 2 de 3 et vous obtenez comme résultat : 1/6.
4
Réduisez éventuellement la fraction. Si le numérateur et le dénominateur ont un facteur commun, réduisez la fraction en divisant le numérateur et le dénominateur par ce facteur.
- La fraction 5/6 ne peut être réduite, mais 3/6 est réductible à 1/2, puisque vous pouvez diviser en haut et en bas par 3.
5
Convertissez votre résultat en un nombre fractionnaire. Cela ne sera possible que si le numérateur est supérieur au dénominateur.

Publicité

Méthode 4

Méthode 4 sur 5:
Multiplier et diviser des fractions

1
Multipliez deux fractions est simple. Il suffit de multiplier les numérateurs entre eux et de faire de même avec les dénominateurs.
- Pour multiplier 1/2 et 1/3, vous faites 1 x 1 (numérateurs) et 2 x 3 (dénominateurs), ce qui donne comme résultat : 1/6. Point n'est besoin de dénominateur commun quand vous multipliez. Si possible, réduisez la fraction ou convertissez-la un nombre fractionnaire.
2
Divisez deux fractions en multipliant. En effet, cette opération consiste à établir dans un premier temps l'inverse de la seconde fraction (2/5 a pour inverse 5/2). Ensuite, vous multipliez la première fraction par cette fraction inverse.
- Pour diviser 1/2 par 1/3, il faut en fait multiplier 1/2 par l'inverse de 1/3, soit 3 (3/1), ce qui donne comme résultat : 3/2 (3/1 x 1/2). Si possible, réduisez la fraction ou convertissez-la un nombre fractionnaire.
Publicité

Méthode 5

Méthode 5 sur 5:
S'entrainer avec plusieurs fractions

1
Ne vous laissez pas impressionner par les fractions. Vous êtes maintenant capable de manipuler plusieurs fractions en même temps et des fractions avec de grands nombres ou des inconnues.
2
Additionnez plus de deux fractions. Cela marche aussi pour la soustraction. Vous avez deux possibilités : ou vous vous trouvez le dénominateur commun de toutes les fractions, ou vous le trouvez par paires de fractions successives.
- Vous devez faire la somme : 1/2 + 1/3 + 1/4. Soit vous trouvez dénominateur commun, soit 12 (2 x 3 x4), ce qui donne la somme : 6/12 + 4/12 + 3/12 =13/12, soit vous additionnez les deux premières, ce qui donne, on l'a vu, 5/6, à laquelle vous ajoutez 1/4. Les deux fractions ont comme plus petit dénominateur commun 12, ce qui donne : 10/12 + 3/12 = 13/12. Converti en nombre fractionnaire, vous obtenez : 1 1/12.
Publicité

Conseils

Comme vous le voyez, les fractions ne sont pas très compliquées, à condition de bien maitriser les quatre opérations de base. Il s'agit juste de connaitre les règles de calcul et d'être un peu concentré sur son travail pour ne pas faire d'erreurs.