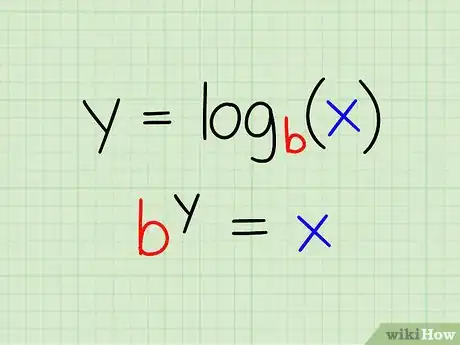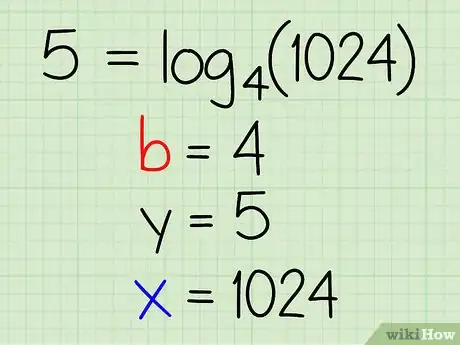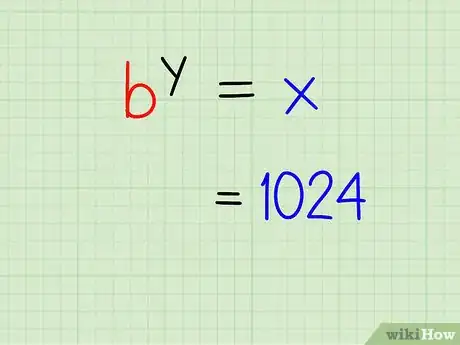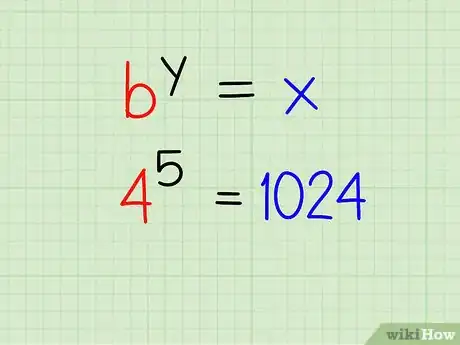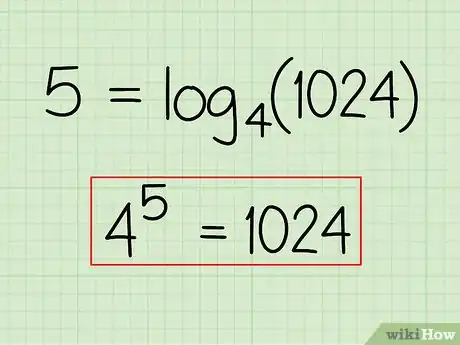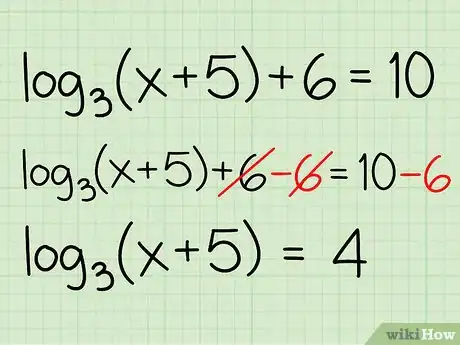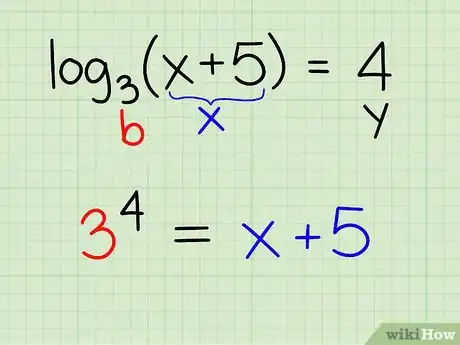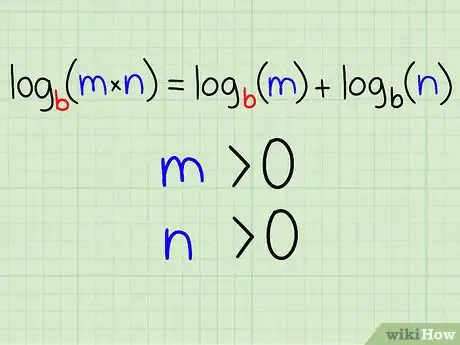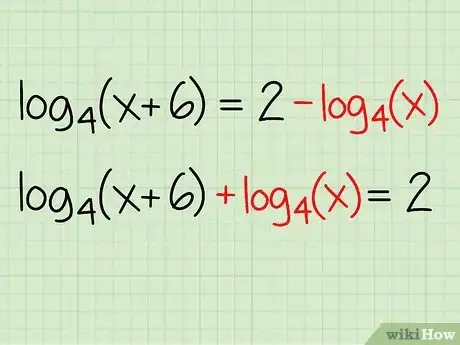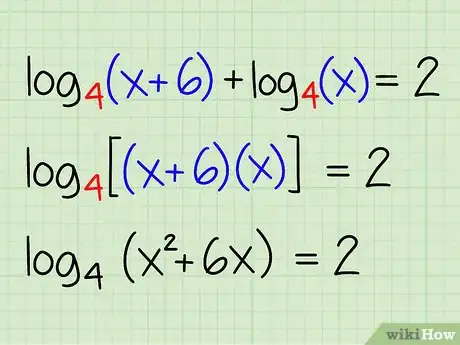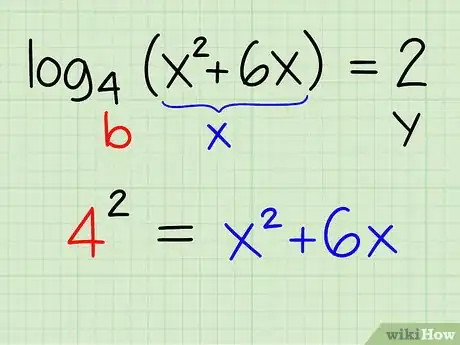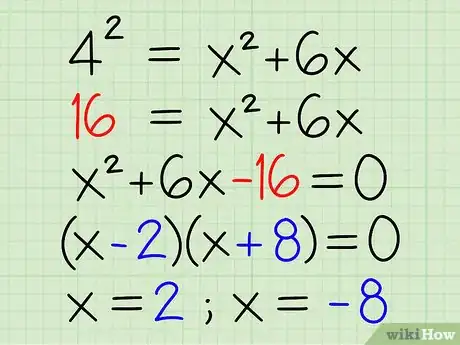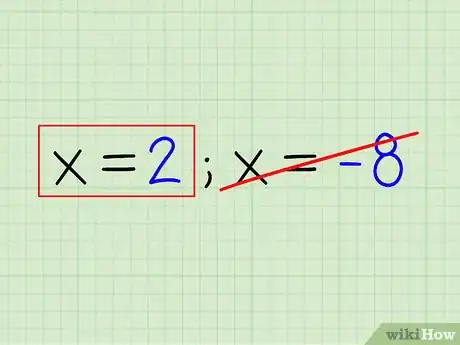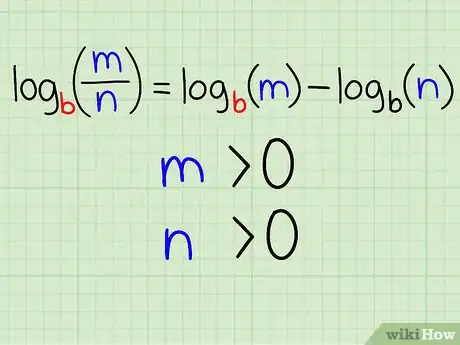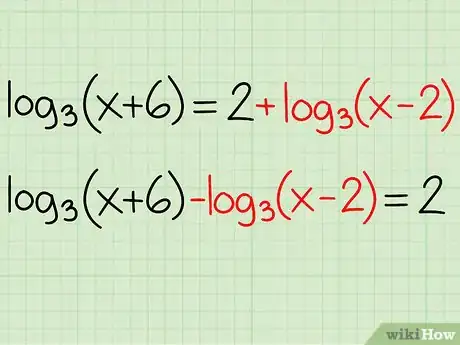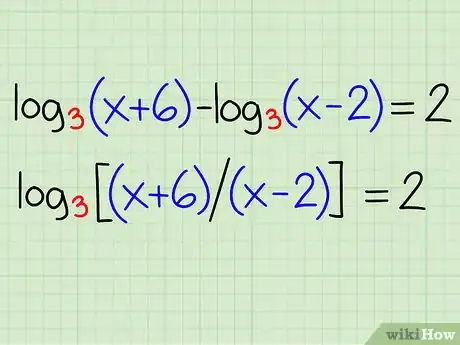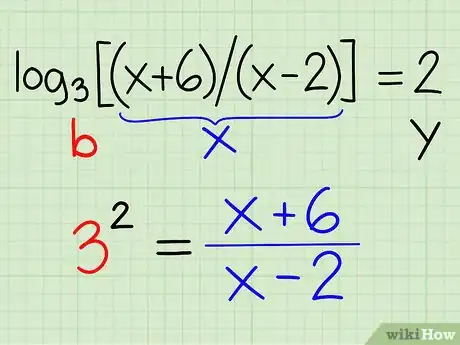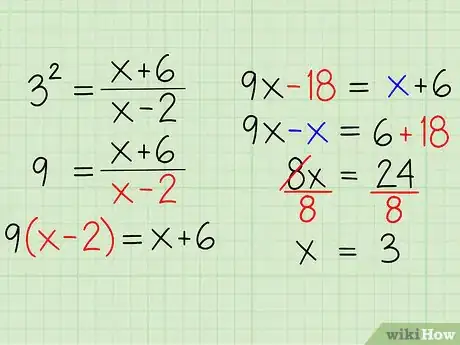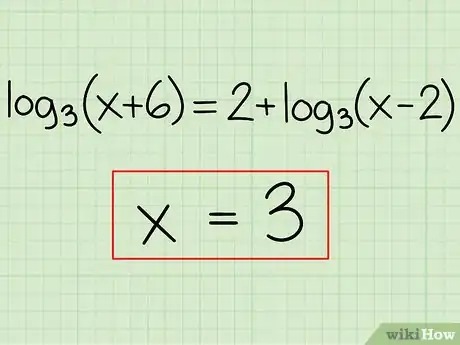wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, des auteur.e.s volontaires ont participé à l'édition et à l'amélioration.
Cet article a été consulté 68 872 fois.
Les équations logarithmiques ne sont pas, au premier abord, ce qu'il y a de plus facile à résoudre en mathématiques, mais elles peuvent être transformées en équations avec des exposants (notation exponentielle). Ainsi, si vous parvenez à effectuer cette transformation et si vous maîtrisez bien le calcul avec les puissances, vous devriez sans peine résoudre ce genre d'équations. NB: on emploiera de temps en temps le terme de « log » en lieu et place de « logarithme », ils sont interchangeables.
Étapes
Méthode 1
Méthode 1 sur 4:Transformer une équation logarithmique en équation avec des puissances[1]
[2]
-
1Commençons par la définition du logarithme. Si vous cherchez à calculer des logarithmes, sachez qu'ils ne sont rien d'autre qu'une façon particulière d'exprimer des puissances. Partons sur une des conditions classiques du logarithme :
-
y = logb (x)
- si et seulement si : by = x
-
b est ce qu'on appelle la base du logarithme. Deux conditions doivent être remplies :
- b > 0 (b doit être strictement positif)
- b ne doit pas être égal à 1
- En notation exponentielle (deuxième équation ci-dessus), y est la puissance et x est ce qu'on appelle l'expression exponentielle, en fait la valeur dont on cherche le log.
-
y = logb (x)
-
2Observez attentivement l'équation. Face à une équation logarithmique, il faut identifier la base (b), la puissance (y) et l'expression exponentielle (x).
-
Exemple : 5 = log4(1024)
- b = 4
- y = 5
- x = 1024
-
Exemple : 5 = log4(1024)
-
3Placez l'expression exponentielle d'un côté de l'équation. Placez, par exemple, votre valeur x à gauche du signe « = ».
- Exemple : 1024 = ?
-
4Élevez la base à la puissance indiquée. La valeur attribuée à la base (b) doit être multipliée par elle-même autant de fois que l'indique la puissance (y).
-
Exemple : 4 x 4 x 4 x 4 x 4 = ?
- En raccourci, cela donne : 45
-
Exemple : 4 x 4 x 4 x 4 x 4 = ?
-
5Récrivez votre réponse. Vous êtes maintenant capable de récrire le logarithme en notation exponentielle. Assurez-vous que votre égalité soit correcte en refaisant le calcul.
- Exemple : 45 = 1024
Publicité
Méthode 2
Méthode 2 sur 4:Trouver x
-
1Isolez le logarithme. Le but est en effet d'isoler dans un premier temps le log. Pour cela, on fait passer tous les membres non logarithmiques de l'autre côté de l'équation. N'oubliez pas d'inverser les signes opératoires !
-
Exemple : log3(x + 5) + 6 = 10
- log3(x + 5) + 6 - 6 = 10 - 6
- log3(x + 5) = 4
-
Exemple : log3(x + 5) + 6 = 10
-
2Récrivez l'équation sous forme exponentielle. Pour pouvoir trouver « x », vous allez devoir passer de la notation logarithmique à la notation exponentielle, cette dernière étant plus facile à résoudre.
-
Exemple : log3(x + 5) = 4
- Partant de l'équation théorique y = logb (x)], appliquons-la à notre exemple : y = 4 ; b = 3 ; x = x + 5
- Récrivez l'équation sous la forme : by = x
- On obtient ici : 34 = x + 5
-
Exemple : log3(x + 5) = 4
-
3Trouvez x. Vous êtes à présent face à une équation du premier degré, qu'il est facile de résoudre. Elle pourrait être du deuxième ou du troisième degré.
-
Exemple : 34 = x + 5
- (3)(3)(3)(3) = x + 5
- 81 = x + 5
- 81 - 5 = x + 5 - 5
- 76 = x
-
Exemple : 34 = x + 5
-
4Inscrivez votre réponse définitive. La valeur que vous avez trouvée pour « x » est la réponse à votre équation logarithmique : log3(x + 5) = 4.
- Exemple : x = 76
Publicité
Méthode 3
Méthode 3 sur 4:Trouver x en utilisant la règle concernant le produit des logarithmes[3]
[4]
-
1Vous devez connaître la règle qui concerne le produit (multiplication) des logs. Selon la première propriété des logs, celle qui concerne le produit des logs (de même base s'entend !), le log d'un produit est égal à la somme des logs des éléments du produit. Illustration :
- logb(m x n) = logb(m) + logb(n)
- Deux conditions doivent être remplies :
- m > 0
- n > 0
-
2Isolez les logs sur un des côtés de l'équation. Le but est en effet d'isoler dans un premier temps les logs. Pour cela, on fait passer tous les membres non logarithmiques de l'autre côté de l'équation. N'oubliez pas d'inverser les signes opératoires !
-
Exemple : log4(x + 6) = 2 - log4(x)
- log4(x + 6) + log4(x) = 2 - log4(x) + log4(x)
- log4(x + 6) + log4(x) = 2
-
Exemple : log4(x + 6) = 2 - log4(x)
-
3Appliquez la règle concernant le produit des logs. Ici, on va l'appliquer en sens inverse, à savoir que la somme des logs est égale au log du produit. Ce qui nous donne :
-
Exemple : log4(x + 6) + log4(x) = 2
- log4[(x + 6)(x)] = 2
- log4(x2 + 6x) = 2
-
Exemple : log4(x + 6) + log4(x) = 2
-
4Récrivez l'équation avec des puissances. Rappelons qu'une équation logarithmique peut être transformée en équation avec des exposants. Comme précédemment, on va passer à la notation exponentielle pour faciliter la résolution du problème.
-
Exemple : log4(x2 + 6x) = 2
- Partant de l'équation théorique [y = logb (x)], appliquons-la à notre exemple : y = 2 ; b = 4 ; x = x2 + 6x
- Récrivez l'équation sous la forme : by = x
- 42 = x2 + 6x
-
Exemple : log4(x2 + 6x) = 2
-
5Trouvez x. Vous êtes à présent face à une équation du second degré, qu'il est facile de résoudre.
-
Exemple : 42 = x2 + 6x
- (4)(4) = x2 + 6x
- 16 = x2 + 6x
- 16 - 16 = x2 + 6x - 16
- 0 = x2 + 6x - 16
- 0 = (x - 2)(x + 8)
- x = 2 ; x = -8
-
Exemple : 42 = x2 + 6x
-
6Inscrivez votre réponse. Souvent, on a deux réponses (racines). Il faut vérifier dans l'équation de départ si ces deux valeurs conviennent. En effet, on ne peut calculer le log d'un nombre négatif ! Inscrivez la seule réponse valable.
- Exemple : x = 2
- On ne le rappellera jamais assez : le log d'un nombre négatif n'existe pas, vous pouvez donc, ici, écarter - 8 comme solution. Si on prenait -8 comme réponse, dans l'équation de base, on aurait : log4(-8 + 6) = 2 - log4(-8), soit log4(-2) = 2 - log4(-8). Impossible de calculer le log d'une valeur négative !
Publicité
Méthode 4
Méthode 4 sur 4:Trouver x en utilisant t la règle concernant le quotient des logarithmes[5]
-
1Vous devez connaître la règle qui concerne la division des logs. Selon la seconde propriété des logs, celle qui concerne la division des logs (de même base s'entend !), le log d'un quotient est égal à la différence du log du numérateur et du log du dénominateur. Illustration :
- logb(m / n) = logb(m) - logb(n)
- Deux conditions doivent être remplies :
- m > 0
- n > 0
-
2Isolez les logs sur un des côtés de l'équation. Le but est en effet d'isoler dans un premier temps les logs. Pour cela, on fait passer tous les membres non logarithmiques de l'autre côté de l'équation. N'oubliez pas d'inverser les signes opératoires !
-
Exemple : log3(x + 6) = 2 + log3(x - 2)
- log3(x + 6) - log3(x - 2) = 2 + log3(x - 2) - log3(x - 2)
- log3(x + 6) - log3(x - 2) = 2
-
Exemple : log3(x + 6) = 2 + log3(x - 2)
-
3Appliquez la règle concernant le quotient des logs. Ici, on va l'appliquer en sens inverse, à savoir que la différence des logs est égale au log du quotient. Ce qui nous donne :
-
Exemple : log3(x + 6) - log3(x - 2) = 2
- log3[(x + 6) / (x - 2)] = 2
-
Exemple : log3(x + 6) - log3(x - 2) = 2
-
4Récrivez l'équation avec des puissances. Rappelons qu'une équation logarithmique peut être transformée en équation avec des exposants. Comme précédemment, on va passer à la notation exponentielle pour faciliter la résolution du problème.
-
Exemple : log3[(x + 6) / (x - 2)] = 2
- Partant de l'équation théorique [y = logb (x)], appliquons-la à notre exemple : y = 2 ; b = 3 ; x = (x + 6) / (x - 2)
- Récrivez l'équation sous la forme : by = x
- 32 = (x + 6) / (x - 2)
-
Exemple : log3[(x + 6) / (x - 2)] = 2
-
5Trouvez x. Maintenant qu'il n'y a plus de logs, mais des puissances, vous devriez trouver facilement x.
-
Exemple : 32 = (x + 6) / (x - 2)
- (3)(3) = (x + 6) / (x - 2)
- 9 = (x + 6) / (x - 2)
- 9(x - 2) = [(x + 6) / (x - 2)](x - 2) &mdash ; on multiplie des deux côtés par (x - 2)
- 9x - 18 = x + 6
- 9x - x - 18 + 18 = x - x + 6 + 18
- 8x = 24
- 8x / 8 = 24 / 8
- x = 3
-
Exemple : 32 = (x + 6) / (x - 2)
-
6Inscrivez votre réponse définitive. Reprenez vos calculs et faites une vérification. Quand vous êtes sûr de votre réponse, inscrivez-la définitivement.
- Exemple : x = 3
Publicité
Références
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut43_logfun.htm#logdef
- ↑ http://www.mathsisfun.com/algebra/logarithms.html
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut46_logeq.htm
- ↑ http://dl.uncw.edu/digilib/mathematics/algebra/mat111hb/eandl/equations/equations.html
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut44_logprop.htm