Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 11 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 3 078 fois.
Une inégalité du second degré contient par définition un terme . La représentation graphique de l’ensemble des solutions se définit par rapport à une parabole, laquelle coupe souvent, mais pas toujours, l’axe des abscisses en deux points : ce sont les racines de l’équation associée. L’ensemble des solutions de l’inéquation est souvent une zone qui contient des points qui vérifient l’inéquation de départ. La définition de ces solutions peut se faire de façon algébrique, comme graphique.
Étapes
Partie 1
Partie 1 sur 4:Factoriser une inéquation
-
1Si ce n’est pas déjà fait, récrivez l’inégalité sous sa forme développée. Par cette dernière expression, on entend une inégalité qui se présente sous la forme suivante : , dans laquelle , sont des coefficients et , une constante. Le coefficient doit être non nul () [1] .
- C’est ainsi que l’inégalité n’est pas sous sa forme développée, mais factorisée. Vous devez dans un premier temps développer le premier produit en multipliant par chacun des éléments de . Vous soustrairez ensuite 21 de chaque côté de l’inégalité afin d’avoir 0 à droite, ce qui donne :
- C’est ainsi que l’inégalité n’est pas sous sa forme développée, mais factorisée. Vous devez dans un premier temps développer le premier produit en multipliant par chacun des éléments de . Vous soustrairez ensuite 21 de chaque côté de l’inégalité afin d’avoir 0 à droite, ce qui donne :
-
2Factorisez le premier terme. Vous devez donc trouver deux facteurs dont le produit est égal au premier terme. L’objectif final est de transformer l’inégalité en un produit de binômes. Un binôme est un polynôme composé de deux termes [2] . En fait, il faut faire le travail inverse du développement d’un produit de binômes. La première étape consiste donc ici à trouver les deux facteurs qui, multipliés, donnent le premier terme du trinôme.
- Le premier terme est donc : l’affaire est ici simple dans la mesure où seul le produit est égal à . Il est aussi possible d’avoir : .
-
3Trouvez les deux bons facteurs. Il faut en trouver deux dont le produit est égal au troisième terme de l’inégalité. Il faut également que leur somme soit égale au coefficient du milieu. En fait, vous devez établir la liste de tous les facteurs du troisième terme, et, par tâtonnements et calculs rapides, trouver la paire qui donne la bonne somme. Les signes de ces deux facteurs ont toute leur importance aussi bien pour le produit que pour la somme.
- Reprenons notre exemple :
- -21 peut être le produit de 7 et -3 ou de -7 et 3
(). - Il vous faut maintenant vérifier que la somme des deux facteurs trouvés (7 et -3 ou -7 et 3) est le coefficient du terme du milieu. Seule la première paire a pour somme 4, puisque (), la seconde paire donne une somme de -4 ().
- Étant donné que , ces deux facteurs sont les bons puisqu’ils satisfont et le produit et la somme. L’inégalité factorisée est donc la suivante : .
- -21 peut être le produit de 7 et -3 ou de -7 et 3
Publicité - Reprenons notre exemple :
Partie 2
Partie 2 sur 4:Déterminer les racines d’une inégalité
-
1Voyez si les facteurs ont le même signe. Nous avons transformé l’inéquation en un produit de binômes, intéressons-nous au signe de celui-ci. Si une inégalité est positive, cela signifie soit que les deux binômes sont positifs, soit qu’ils sont négatifs. Par contre, si l’inégalité est négative, cela signifie que les deux binômes sont de signes opposés [3] .
- L’inégalité peut être large, c’est-à-dire comporter le signe ou , cela signifie donc qu’il faut envisager le cas où le produit soit nul, ce qui peut advenir dans deux cas : ou un des binômes est nul ou les deux le sont.
- Dans notre exemple, nous avons transformé l’inéquation en un produit de binômes, puisque . En conséquence, les deux binômes sont de signes opposés, mais lequel est positif, lequel est négatif ?
-
2Déterminez le signe de chacun des binômes. Pour pouvoir trouver l’ensemble des solutions, vous devez en fonction du symbole de l’inégalité, déterminer les signes possibles des deux binômes. C’est comme cela que, si l’inéquation est négative, vos deux binômes devront être de signe opposé, ce qui fait deux possibilités : l’un des deux doit être négatif, tandis que l’autre doit être positif. Nous vous rappelons quel produit d’un nombre négatif par un nombre positif est négatif.
- Pour rappel, l’inégalité peut être large, c’est-à-dire comporter le signe ou , cela signifie donc qu’il faut envisager le cas où le produit soit nul, ce qui peut advenir dans deux cas : ou un des binômes est nul ou les deux le sont.
- Reprenons notre exemple. Nous avons : le produit des facteurs est donc négatif, les binômes et sont donc de signes opposés.
-
3Inscrivez les différentes possibilités. Quel que soit le cas de figure de l’inégalité, il n’y a que deux possibilités : soit le trinôme doit être positif et les deux binômes sont de même signe (positif ou négatif), soit il doit être négatif et les deux binômes doivent être de signes opposés [4] .
- Dans notre cas concret, le produit de binômes ( ) doit être négatif. Pour remplir cette condition, les binômes doivent être de signes opposés, ce qui donne les deux possibilités suivantes :
ET (le premier binôme étant négatif, le second se doit d’être positif)
OU
ET (le premier binôme étant positif, le second se doit d’être négatif).
- Dans notre cas concret, le produit de binômes ( ) doit être négatif. Pour remplir cette condition, les binômes doivent être de signes opposés, ce qui donne les deux possibilités suivantes :
-
4Trouvez les valeurs respectives de . Pour chaque possibilité, vous devez déterminer l’ensemble des solutions des différentes inégalités, ce qui revient à isoler . Toute modification faite à un membre d’une inégalité doit l’être aussi dans l’autre membre et à l’identique [5] .
- La première possibilité consisterait à avoir ET .
- Si , alors en ajoutant -7 de chaque côté, on obtient :
,
soit . - Dans le même cas de figure, le second binôme () doit être positif. On ajoute 3 de chaque côté et l’on obtient :
,
soit .
- Si , alors en ajoutant -7 de chaque côté, on obtient :
- Dans ce premier cas, donc, vous devez voir s’il existe des valeurs telles que et .
- La première possibilité consisterait à avoir ET .
-
5Vérifiez la cohérence de vos réponses. Vous obtenez deux ensembles de solutions avec vos deux binômes, mais pour résoudre l’inéquation de départ, l’union de deux ensembles de solutions ne doit pas être vide. Si c’était le cas alors, votre hypothèse de départ sur les signes des binômes serait fausse [6] .
- Ainsi, la première double condition est et . Vous devez vous demander s’il existe une réponse à cette double condition. Existe-t-il une ou plusieurs valeurs telles que soit inférieur à -7 tout en étant supérieur à 3 ? La réponse est bien évidemment non, donc cette solution n’est pas la bonne.
-
6Envisagez la seconde possibilité. Si la première possibilité s’avérait impossible, vous devriez tester la seconde hypothèse, les signes des binômes ont été intervertis. Procédez de la même façon en isolant et en modifiant dans les mêmes termes les deux membres des inéquations [7] .
- La seconde combinaison pour obtenir est que ET .
- Simplifiez la première condition en soustrayant 7 de chaque côté, ce qui donne :
- Simplifiez la seconde condition en ajoutant 3 de chaque côté, ce qui donne :
- Simplifiez la première condition en soustrayant 7 de chaque côté, ce qui donne :
- La seconde combinaison se présente donc ainsi : et .
- La seconde combinaison pour obtenir est que ET .
-
7Vérifiez l’existence d’un ensemble de réponses. Comme pour la première combinaison, vous devez voir si les inégalités admettent une ou plusieurs solutions. Si ce n’est pas le cas, alors, la fonction de départ n’admettra aucun solution [8] .
- La seconde combinaison pour obtenir est que ET . Cette fois-ci, les deux conditions ont un ensemble de réponses commun : il regroupe toutes les valeurs de comprise entre et , ces deux valeurs n’étant pas prises. Ainsi, la valeur 0 satisfait l’inéquation de départ. Il est important de bien regarder le symbole de l’inégalité pour savoir s’il faut ou non retenir les racines de l’équation.
Publicité
Partie 3
Partie 3 sur 4:Présenter sur un axe l’ensemble des solutions
-
1Tracez un axe gradué. À moins que des conditions particulières ne vous aient été spécifiées, tracez un simple axe horizontal gradué. Ce à quoi vous devez veiller, c’est que les deux racines des binômes soient sur l’axe, n’hésitez pas à ajouter deux ou d'autres unités de part et d’autre afin d’avoir une vision claire de l’ensemble des solutions.
- Les solutions de sont, comme on l’a démontré précédemment, et . Pour trouver l’ensemble des solutions, vous devez tracer un axe horizontal gradué et y placer les points -7 et 3.
-
2Sur l’axe, repérez, puis marquez les deux racines des binômes. Sur ces deux points, vous allez faire figurer un crochet qui indiquera si oui ou non, vous prenez la valeur en question. Si l’inégalité est strictement supérieure () à une valeur, le crochet sera ouvert vers la gauche, mais si elle strictement inférieure (), il sera ouvert vers la droite. En cas d’inégalité large ( ou ), comme les valeurs sont incluses dans les réponses, les crochets seront respectivement inversés [9] .
- Dans notre exemple, les solutions sont donc et , le crochet de 7 est ouvert sur la gauche et celui sur le 3, l’est sur la droite.
-
3Tracez les ensembles de solutions des binômes. À partir d’une des racines, tracez sur l’axe un trait de couleur pour montrer les solutions de la première inégalité binomiale. Ainsi si les solutions sont inférieures à la racine vous tirerez un trait vers la gauche, vers la droite si elles sont supérieures. Prenez un crayon d’une autre couleur et faites exactement la même chose avec l’autre racine. Pour une plus grande lisibilité, il est de coutume de tracer ces deux traits, l’un au-dessus de l’axe gradué, l’autre au-dessous. C’est une étape délicate et il ne faut pas vous tromper si vous voulez résoudre correctement l’inéquation de départ.
- Dans notre exemple, nous avons retenu l’hypothèse que devait être supérieur à -7 tout en étant inférieur à 3. Donc, assez logiquement, toutes les valeurs comprises entre ces deux racines satisfont l’inéquation de départ.
Publicité
Partie 4
Partie 4 sur 4:Représenter graphiquement l’ensemble des solutions
-
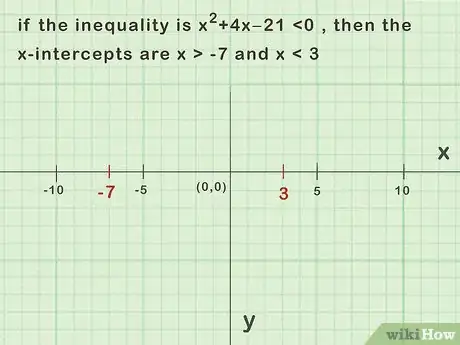
1Placez les points d’intersection de la parabole et de l’axe des abscisses. Le plus souvent, une parabole coupe cet axe en deux points, car il y a deux racines au trinôme [10] .
- L’inégalité de départ était donc et nous avons trouvé que le trinôme admettait deux racines et : ce sont les abscisses avec lesquelles le trinôme s’annule. Ces deux abscisses sont celles des points d’intersection de la parabole avec l’axe des « x ».
-
2Déterminez l’axe de symétrie. Ce dernier est la ligne qui partage verticalement la parabole en deux parties égales. L’équation de cet axe de symétrie est toujours : , équation dans laquelle et sont les deux coefficients respectifs de l’inconnue dans la fonction d’origine [11] .
- Nous avions donc l’inégalité , l’équation de l’axe de symétrie de la parabole est , soit ou . L’axe de symétrie est donc la droite d’équation .
-
3Déterminez le sommet de la parabole. Le sommet est soit le minimum soit le maximum de la parabole, tout dépend de son orientation. Il se trouve forcément sur l’axe de symétrie, donc on connait forcément son abscisse. Il ne reste plus qu’à calculer l’ordonnée en remplaçant dans l’équation de départ par la valeur trouvée pour l’axe de symétrie [12] .
- Dans notre exemple, l’axe de symétrie a pour équation . Dans l’équation de départ, remplacez par -2 et faites les calculs, ce qui donne :
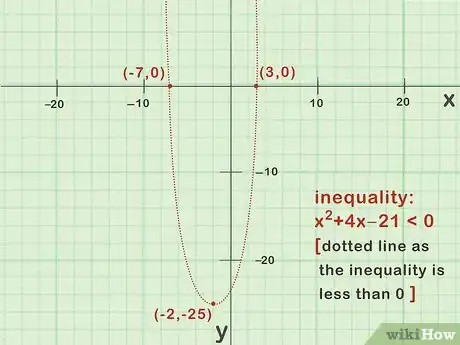
Ainsi, le sommet de la parabole est le point de coordonnées .
- Dans notre exemple, l’axe de symétrie a pour équation . Dans l’équation de départ, remplacez par -2 et faites les calculs, ce qui donne :
-
4Déterminez la direction de la parabole. Pour savoir dans quel sens s’ouvre la parabole, il faut regarder le signe de de l’inégalité de départ, en forme développée s’entend. Si est positif, la parabole va en s’ouvrant vers le haut. Si est négatif, c’est l’inverse : la parabole va en s’ouvrant vers le bas [13] .
- Dans l’inégalité , , soit 1, est positif : la parabole s’ouvre vers le haut.
-
5Tracez la parabole avec un trait plein ou pointillé. Si l’inégalité est large ( ou ), tracez une parabole en trait plein, signifiant par là que vous prenez les points de la courbe de l’ensemble des réponses. Si l’inégalité est stricte ( ou ), tracez une parabole en trait pointillé, signifiant par là que vous excluez les points de la courbe de l’ensemble des réponses [14] .
- La parabole d’équation doit être tracée en pointillés, car l’inégalité est stricte : les points de la courbe sont exclus.
-
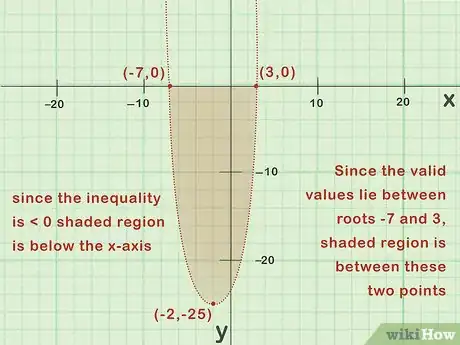
6Hachurez l’ensemble des réponses. Comme une inéquation admet comme solutions un ensemble de points, cela correspondra à une zone du graphe que l’on mettra en évidence par des hachures. Le plus dur est maintenant de déterminer quelle zone doit être hachurée. Si l’inégalité de départ est négative, vous hachurerez une zone sous l’axe des abscisses, sinon faites-le au-dessus [15] . Dans les deux cas, il reste à savoir s’il faut hachurer l’intérieur ou l’extérieur de la parabole. C’est là qu’intervient le travail de la partie précédente : si les solutions étaient entre les deux racines, vous hachureriez l’intérieur de la parabole. Si ce n’était pas le cas, vous hachureriez l’extérieur de la parabole [16] .
- Pour l’inéquation qui est négative, vous hachurerez sous l’axe des abscisses et comme les solutions sont comprises entre les racines -7 et 3, vous hachurerez la zone entre ces deux points, à l’intérieur de la parabole.
Publicité
Références
- ↑ http://www.mathsisfun.com/algebra/quadratic-equation.html
- ↑ http://www.mathwarehouse.com/dictionary/B-words/what-is-a-binomial.php
- ↑ https://www.khanacademy.org/math/algebra-home/alg-quadratics/alg-quadratic-inequalities/v/quadratic-inequality-example-2
- ↑ https://www.khanacademy.org/math/algebra-home/alg-quadratics/alg-quadratic-inequalities/v/quadratic-inequality-example-2
- ↑ http://www.purplemath.com/modules/ineqsolv.htm
- ↑ https://www.khanacademy.org/math/algebra-home/alg-quadratics/alg-quadratic-inequalities/v/quadratic-inequality-example-2
- ↑ http://www.purplemath.com/modules/ineqsolv.htm
- ↑ https://www.khanacademy.org/math/algebra-home/alg-quadratics/alg-quadratic-inequalities/v/quadratic-inequality-example-2
- ↑ http://www.bbc.co.uk/schools/gcsebitesize/maths/algebra/inequalitiesrev4.shtml
- ↑ http://www.themathpage.com/aprecalc/roots-zeros-polynomial.htm
- ↑ http://www.virtualnerd.com/algebra-2/quadratics/inequalities/graphing-solving-inequalities/graph-inequality
- ↑ http://www.virtualnerd.com/algebra-2/quadratics/inequalities/graphing-solving-inequalities/graph-inequality
- ↑ http://www.dummies.com/test-prep/act/act-trick-for-quadratics-how-to-quickly-find-the-direction-of-a-parabola/
- ↑ http://www.varsitytutors.com/hotmath/hotmath_help/topics/graphing-quadratic-inequalities
- ↑ https://www.khanacademy.org/math/algebra-home/alg-quadratics/alg-quadratic-inequalities/v/quadratic-inequalities-visual-explanation
- ↑ http://www.purplemath.com/modules/ineqquad.htm













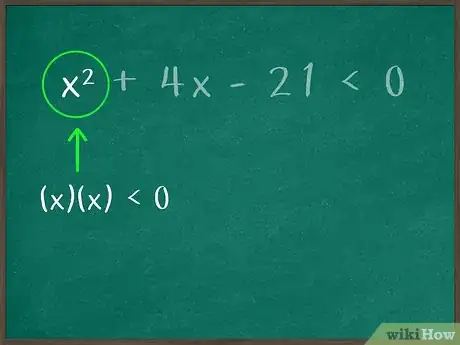















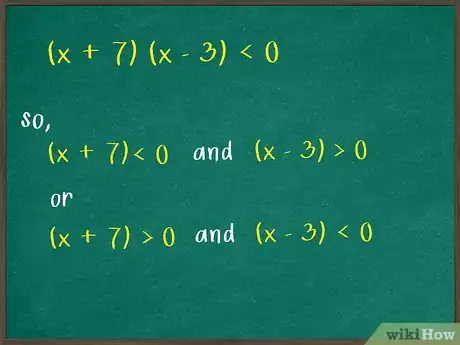















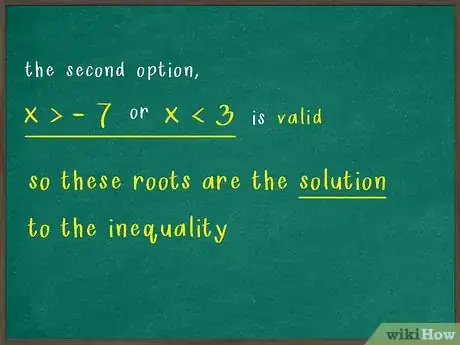


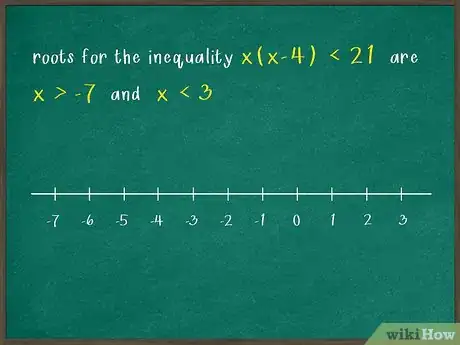
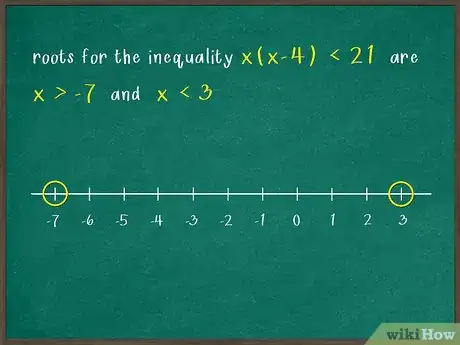

































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 3 078 fois.