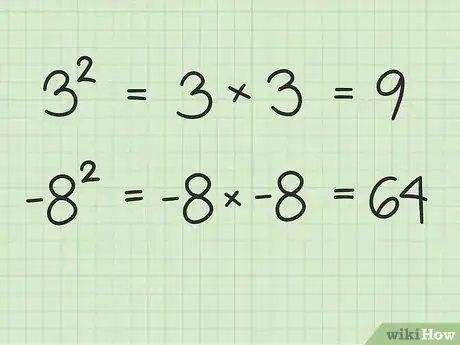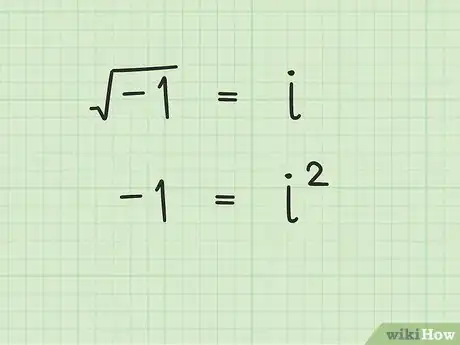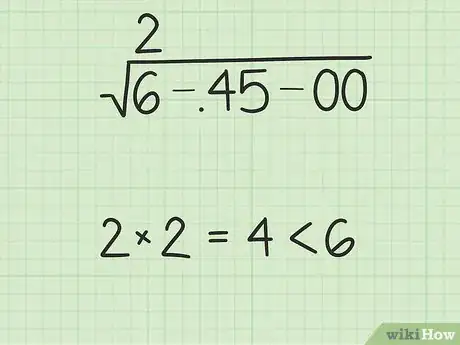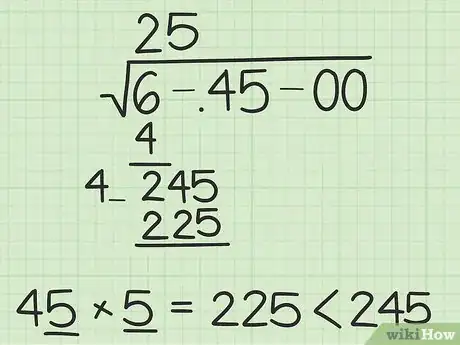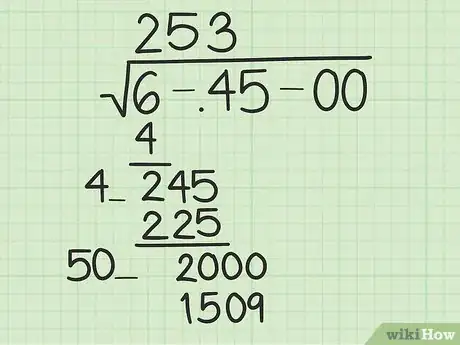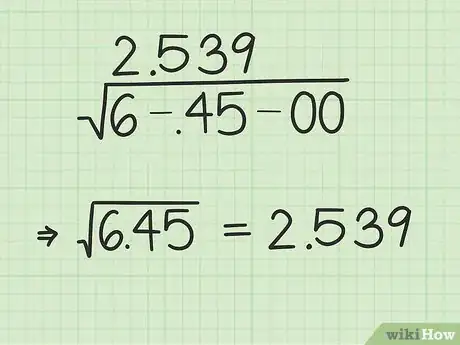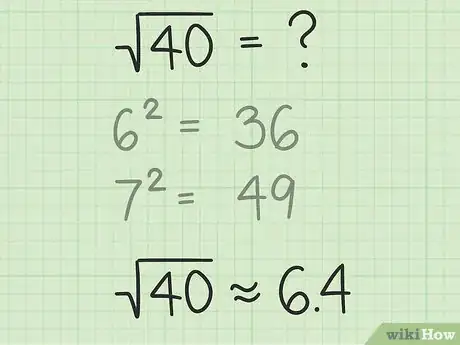Comment résoudre des problèmes contenant des racines carrées

Informations concernant l'auteur.e

À la vue du symbole de la racine carrée, certaines personnes prennent peur, pourtant les problèmes de racines carrées ne sont pas si ardus qu'il y parait. Certaines racines carrées se résolvent aussi facilement qu'une multiplication ou une division. Par contre, il est des problèmes impliquant des racines qui sont de véritables casse-têtes au premier abord, mais si vous savez vous y prendre, là encore ce n'est pas compliqué.

Partie 1

Partie 1 sur 3:
Comprendre les carrés et les racines carrées

1
Élever un nombre au carré consiste à le multiplier par lui-même. Pour comprendre les racines carrées, il faut impérativement savoir ce qu'est un carré. La notion de « carré » est simple à comprendre, prenez un nombre et multipliez-le par lui-même, et vous aurez un carré. Ainsi, 3 au carré est la même chose que 3 fois 3 (= 9) et 9 au carré est équivalent à 9 × 9 = 81. Un carré est indiqué par un petit « 2 » situé en haut et à droite du nombre concerné, on écrit, par exemple, 3², 9², 100², etc.
- Exercez-vous à élever au carré jusqu'à ce que vous compreniez bien le concept. Nous l'avons déjà dit : élever un nombre au carré consiste simplement à le multiplier par lui-même. Les nombres négatifs peuvent aussi s'élever au carré. Par contre, le résultat sera toujours positif (- x - = +). Par exemple, - 8² = - 8 × - 8 = 64.
2
Extraire une racine carrée consiste, « à l'inverse », à retrouver le nombre qui a été élevé au carré. La racine carrée est représentée par un signe opératoire (√, appelé « racine »), c'est en quelque sorte le pendant du petit « 2 » du carré (x²). Quand vous verrez ce symbole de la racine, vous devrez vous poser la question : « quel est ce nombre qui, élevé au carré, peut bien me donner le nombre marqué sous la racine (radicande) ? » Ainsi, pour extraire √(9), vous devez trouver le nombre qui, multiplié par lui-même, donne 9. La réponse est alors « trois », car 3² = 9.
- Autre exemple : cherchons la racine carrée de 25 (√(25)). Trouvez le nombre qui, multiplié par lui-même, donne 25. Comme 5² = 5 × 5 = 25, on peut affirmer que √(25) = 5.
- On a dit précédemment que la racine et le carré s'opposaient. Si les deux sont combinés, ils s'annulent donc. Prenons un exemple : √(64) ou racine carrée de 64. On sait que 64 = 8². On remplace 64 sous la racine par 8² : √(64) = √(8²). Comme racine et carré s'annulent : √(8²)= 8.
3
Faites la différence entre les carrés parfaits et imparfaits. Jusqu'à présent, vous avez rencontré des carrés parfaits, qui correspondent à des entiers. Ce n'est pas cependant pas toujours le cas, le plus souvent, la racine carrée d'un nombre est un chiffre décimal avec beaucoup de décimales. Les nombres qui ont des racines carrées entières (ni fractions, ni décimales) sont dits « carrés parfaits ». Les exemples vus (9, 25 et 64) étaient des carrés parfaits dans la mesure où en prenant leurs racines, on retombait sur des entiers (respectivement 3, 5, et 8).
- Ces nombres dont la racine carrée n'est pas un entier sont appelés carrés imparfaits. La racine de ce genre de carrés donne soit un nombre décimal soit une fraction. Parfois, la calculatrice renvoie un nombre décimal impressionnant. C'est ainsi que √(13) = 3,605551275464…
4
Retenez les 10 à 12 premiers carrés parfaits. Comme vous l'aurez probablement remarqué, extraire la racine carrée d'un carré parfait est facile. En cela, il est peut-être utile de retenir les 10 ou 12 premiers carrés parfaits. On les rencontre assez souvent, cela vous permettra en les apprenant par cœur d'aller plus vite. Les 12 premiers carrés parfaits sont les suivants :
- 1² = 1 × 1 = 1
- 2² = 2 × 2 = 4
- 3² = 3 × 3 = 9
- 4² = 4 × 4 = 16
- 5² = 5 × 5 = 25
- 6² = 6 × 6 = 36
- 7² = 7 × 7 = 49
- 8² = 8 × 8 = 64
- 9² = 9 × 9 = 81
- 10² = 10 × 10 = 100
- 11² = 11 × 11 = 121
- 12² = 12 × 12 = 144
5
Simplifiez vos racines carrées en extrayant, si possible, des carrés parfaits. Résoudre la racine carrée d'un carré imparfait peut s'avérer difficile, surtout si vous n'avez pas de calculatrice sous la main (plus loin, vous trouverez une méthode pour calculer à la main). Il est souvent possible, avant d'opérer le calcul, de simplifier la racine. Il faut toujours voir s'il n'est pas possible de décomposer le radicande en produit de facteurs. Si un des facteurs est un carré parfait, c'est encore mieux, puisqu'on pourra alors le sortir de la racine. Dit comme ça, cela peut sembler compliqué, mais il n'en est rien, lisez plutôt ^{[1]
X
Source de recherche} !
- Admettons que vous ayez à trouver la racine carrée de 900. Pas simple au premier abord ! Cependant, si l'on arrive à décomposer ce nombre en produits de facteurs, la tâche sera simplifiée. Par « facteurs », on entend des nombres qui, multipliés entre eux, donnent un nombre particulier, 900 ici. Prenons un exemple concret : 6 peut s'obtenir en faisant 1 × 6 et 2 × 3. En conséquence, 1, 2, 3 et 6 sont les facteurs de 6.
- Reprenons notre exemple : au lieu de chercher la racine de 900, on va chercher celle de 9 × 100. On le sait, 9 est un carré parfait, on va pouvoir l'isoler, grâce à une propriété de la racine, sous la forme : √(9 × 100) = √(9) × √(100) = 3 × √(100). Provisoirement, on a : √(900) = 3√(100).
- Dans le même ordre d'idées, vous pouvez décomposer 100 en 25 x 4. On a ainsi : √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. En conclusion, √(900) = 3(10) = 30.
6
Passez-en par les nombres imaginaires pour les racines carrées de nombres négatifs. Voyons, quel nombre, multiplié par lui-même, donne -16 ? Assurément, ce n'est ni 4 ni -4 ; si vous les élevez au carré, vous obtenez une seule réponse : 16 ! On abandonne ? Il est strictement impossible d'extraire la racine carrée d'un nombre négatif, -16 ou un autre. Par convention, de telles racines existent et ce sont des nombres dits « imaginaires » (qui s'expriment à l'aide d'une lettre ou d'un symbole). Dans l'ensemble des nombres complexes, il est un nombre imaginaire, appelé « i » dont le carré est -1. Le plus souvent, la racine carrée d'un nombre négatif est un nombre imaginaire (ou à tout le moins qui en contient un).
- On a dit que ces nombres particuliers ne se présentaient pas sous forme chiffrée, mais on peut les manipuler comme tels par contre. C'est ainsi que si on élève au carré ces racines particulières, on obtiendra des nombres négatifs. Ainsi, i² = -1
Publicité

Partie 2

Partie 2 sur 3:
Résoudre en utilisant des algorithmes de type division

1
Transformez votre problème de racine carrée en problème de division. Bien que cela prenne du temps, sachez que vous pouvez extraire la racine d'un carré imparfait à la main. Il faut une méthode de résolution, un algorithme, qui ressemble à une division classique, pas tout à fait cependant ^{[2]
X
Source de recherche} !
- Il faut commencer par présenter votre racine carrée sous la forme d'une division. Admettons que vous ayez à trouver la racine carrée de 6,45, chiffre qui à l'évidence n'est pas un carré parfait. Commencez par inscrire le symbole de la racine (√), puis le radicande. Ce dernier est bien « à l'abri » sous la barre de la racine, cela ressemble à une division, non ? Vous avez ainsi une racine carrée, √, avec une longue barre horizontale, sous laquelle vous noterez 6,45.
- Nous allons inscrire des nombres au-dessus, aussi prévoyez de la place.
2
Groupez les chiffres par paires. Pour commencer, on groupe les chiffres par deux sous la barre de la racine en commençant par la virgule. Vous pouvez mettre une petite marque entre les paires (un point, une barre oblique, une virgule) pour bien les identifier.
- Reprenons notre exemple : 6,45 subdivisé en paires pourrait ressembler à : 6-,45-00. Notez que la première paire se réduit à un seul chiffre, nombre de départ oblige, c'est normal !
3
Trouvez ensuite le plus grand nombre entier dont le carré est inférieur ou égal à la première paire. Commencez par la paire de gauche. Trouvez le plus grand nombre entier dont le carré est inférieur ou égal à cette première paire. Par exemple, si vous avez 37, vous prendrez 6, parce que 6² = 36 et que 36 < 37. 7 n'irait pas, car 7² = 49 et 49 > 37. Inscrivez cette réponse au-dessus et à l'aplomb de cette paire. Ce sera le premier chiffre de la réponse définitive.
- Reprenons notre exemple : la première paire de 6-,45-00 est 6 (06). Le plus grand nombre qui élevé au carré donne 6 ou moins de 6 est 2 ; 2² = 4. Inscrivez un "2" au-dessus du 6 du radicande.
4
Prenez le double de la réponse que vous venez de trouver, inscrivez-le en dessous et faites la soustraction. Reprenez ce premier chiffre trouvé et doublez-le. Ce résultat, vous l'inscrirez cette fois-ci en dessous de la paire en question. Faites la différence entre les deux. Ensuite, vous abaisserez la paire suivante au niveau du résultat de la soustraction. Enfin, vous inscrivez à gauche de ce nombre, le dernier chiffre du résultat doublé précédemment, en laissant un espace entre.
- Reprenons notre exemple : calculez le double du premier résultat (2), soit 2 × 2 = 4. Puis, vous soustrayez ce résultat de la première paire (6), ce qui donne : 6 - 4 = 2. Ensuite, vous abaissez la paire suivante (45) au niveau du résultat de la soustraction, ce qui donne 245. Enfin, vous devez inscrire une nouvelle fois 4, mais à gauche de 245 en laissant un espace entre les deux, comme ceci : 4_.
5
Remplissez l'espace laissé libre. On en arrive à l'étape un peu délicate qui consiste à trouver la valeur qu'il faut mettre à la place de l'espace laissé vacant. Vous devez le nombre qui, multiplié par votre nombre de gauche, donnera un résultat égal ou inférieur au nombre « abaissé », situé à droite de l'espace vacant. Admettons que vous ayez, après abaissement, 1 700 et que le nombre de gauche soit 40_, vous devrez mettre « 4 », car 404 × 4 = 1 616, lequel nombre est inférieur à 1 700, alors que 405 × 5 = 2 025 (supérieur à 1 700). Ce chiffre sera le deuxième chiffre de votre réponse finale, vous devez le mettre au-dessus de la barre de la racine, à côté du premier.
- Reprenons notre exemple : vous devez trouver un chiffre (y) à mettre dans l'espace vacant de telle sorte que le produit 4y × y donne un résultat proche de 245, mais non supérieur. La réponse est ici 5. En effet, 45 × 5 = 225, alors que 46 × 6 = 276.
6
Continuez sur ce même principe (trouver le chiffre manquant) pour trouver les autres chiffres de la racine. Soustrayez le nombre inférieur (issu de la multiplication) du nombre en place. Placez le double du nombre situé au-dessus de la barre de la racine à gauche du résultat de la soustraction, en n'oubliant pas l'espace vacant. Renouvelez ces étapes jusqu'à obtenir 0 ou le nombre de décimales demandé.
- Si nous reprenons notre exemple, nous soustrayons 225 de 245, ce qui donne 20. On abaisse ensuite la dernière paire, 00, pour obtenir 2 000. On double le résultat précédent, soit 25 × 2 = 50. Vous devez trouver le chiffre à mettre à la place de l'espace vacant pour que 50_ × _ soit inférieur ou égal à 2 000. C'est 3 (503 x 3 = 1 509). Désormais, vous avez "253" au-dessus de la barre de la racine, si vous continuiez, le quatrième chiffre serait 9.
7
Déplacez la virgule verticalement vers le haut depuis le radicande. Vous avez les chiffres significatifs, il ne reste plus qu'à placer la virgule au bon endroit. C'est très simple, il suffit de mettre la virgule à l'aplomb de la virgule du radicande. Par exemple, vous avez le radicande 49,8, la virgule de la racine sera placée juste au-dessus, entre les deux chiffres positionnés au-dessus du 9 et du 8.
- Reprenons notre exemple : le radicande est 6,45, les deux chiffres du haut alignés sur le 6 et le 4 sont respectivement le 2 et le 5. La virgule se place donc entre ces deux chiffres et la racine carrée de 6,45 est 2,539.
Publicité

Partie 3

Partie 3 sur 3:
Estimer approximativement la racine d'un carré imparfait

1
Trouvez la racine d'un carré imparfait par approximation. Une fois les principaux carrés parfaits mémorisés, résoudre les racines carrées des carrés imparfaits devient plus facile. Comme vous connaissez un certain nombre de carrés parfaits, vous pouvez, par encadrement et par approximations successives, trouver les racines des carrés imparfaits. On commence toujours par trouver les deux carrés parfaits qui encadrent le nombre dont on vous demande la racine. Ensuite, déterminez celui des deux carrés qui se trouve être le plus proche du nombre de référence.
- Admettons qu'il vous faille extraire la racine carrée de 40. Si vous connaissez vos carrés parfaits, vous saurez vite 40 est compris entre 6² (36) et 7² (49). 40 étant supérieur à 6², sa racine carrée sera supérieure à 6, et comme 40 est inférieur à 7², sa racine carrée sera inférieure à 7. 40 étant plus près de 36 que de 49, la racine de 40 sera plus près de 6 que de 7. Plus loin, nous verrons comment on affine la réponse.
2
Affinez la réponse à une décimale. Une fois les deux carrés parfaits entourant votre nombre trouvés, il faut simplement faire preuve de logique pour affiner progressivement votre réponse — plus vous affinerez, plus vous approcherez de la bonne réponse. On commence par affiner au « dixième », le choix du bon dixième relève de la logique, aussi vous n'aurez pas à essayer toutes les décimales.
- Reprenons notre exemple : la racine carrée de 40 est plus proche de 36 (racine = 6) que de 49 (racine = 7). Essayons alors 6,4.
3
Multipliez cette approximation par elle-même. Maintenant, vous allez élever au carré votre estimation. À moins d'avoir beaucoup de chance, il est fort peu probable que vous tombiez sur la bonne réponse, vous serez soit en dessous soit au-dessus. Dans le premier cas, vous devrez revoir votre estimation à la hausse et à la baisse dans le deuxième.
- Multipliez 6,4 par lui-même, ce qui donne : 6,4 × 6,4 = 40,96, soit légèrement au-dessus de 40, notre radicande.
- Si le carré de votre estimation dépasse votre nombre, il faut diminuer d'un dixième l'estimation. On prendra ici 6,3, ce qui donne 6,3 × 6,3 = 39,69. Cette fois, nous sommes en dessous de 40, donc la racine de 40 est quelque part entre 6,3 et 6,4. 40 étant plus porche de 69,6 que de 40,96, la racine de 40 est plus proche de 6,3 que 6,4.
4
Continuez à raisonner sur ce principe. Selon ce qu'on vous a demandé, vous pouvez soit vous arrêter à cette estimation (6,3) soit affiner davantage. Vous devez alors estimer les « centièmes » en utilisant le même principe et en faisant les mêmes calculs. Vous pouvez ainsi, par approches successives, déterminer 4, 5, 6… décimales, tout dépendra du degré de précision que vous voulez ou qu'on vous demande.
- Reprenons notre exemple : posez que 6,33 est votre estimation à deux décimales. Multipliez 6,33 par lui-même : 6,33 × 6,33 = 40,0689. Comme on est encore un peu au-dessus du nombre de départ, on peut essayer 6,32. Donc, on fait : 6,32 × 6,32 = 39,9424. Cette fois, nous sommes en dessous de notre nombre. Nous pouvons donc affirmer sans nous tromper que la racine carrée de 40 se situe entre 6,32 et 6,33. Si le cœur vous en dit, vous pouvez continuer sur cette voie, avec 3 ou davantage de décimales. Vous approcherez ainsi de plus en plus de votre nombre de référence.
Publicité

Conseils

Pour aller vite, prenez une calculatrice. En effet, toutes les calculatrices dignes de ce nom savent calculer les racines carrées. Le plus souvent, il faut taper le radicande à l'aide des touches numériques, puis appuyer sur la touche de la racine carrée. Ainsi, pour trouver la valeur de la racine carrée de 841, vous taperez 8, 4 et 1, puis vous appuierez sur la touche (√), ce qui vous donnera comme réponse : 39.