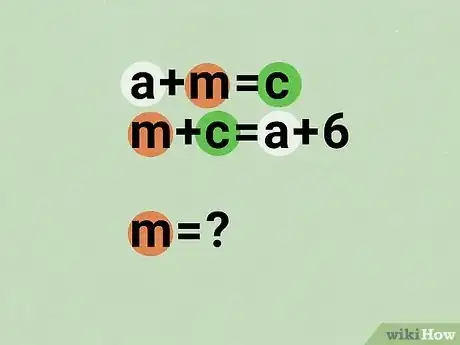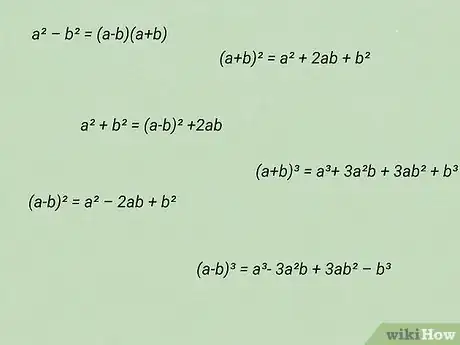Comment résoudre les problèmes de mathématique

Coécrit par Daron Cam

Les mathématiques sont un domaine très vaste (algèbre, géométrie, trigonométrie…) et il est logique que les modes de résolution soient adaptés. Pourtant, il est des façons de procéder, surtout en début de travail, communes à toutes ces branches. Il serait dommageable de ne pas les mettre en œuvre systématiquement. Ces méthodes d'approche permettent certes de résoudre les problèmes, mais elles vous permettent d'accéder à la nature profonde de cette science. Une fois cette première étape passée, vous pourrez déployer des méthodes plus spécifiques de résolution.

Partie 1
Partie 1 sur 3:
Comprendre un problème de mathématiques

  1. Image intitulée Solve Math Problems Step 1
    1
    Sachez à quoi rattacher votre exercice. S'agit-il d'un simple exercice d'algèbre, de trigonométrie, d'une équation du second degré ? Peut-être deux domaines des mathématiques sont-ils sous-jacents ? Avant de commencer à résoudre quoi que ce soit, identifiez le domaine concerné afin de vous remémorer (ou de réviser) ce chapitre particulier.
  2. Image intitulée Solve Math Problems Step 2
    2
    Lisez attentivement le libellé du problème. Quand bien même l'exercice ou le problème parait simple, il faut le lire doucement du début à la fin, ne sait-on jamais s'il y a une consigne particulière ou un piège ! Cette consigne est d'autant plus vraie quand le problème est d'emblée long et en apparence complexe. Ce temps passé à bien étudier les termes du problème n'est pas du temps perdu, bien au contraire [1]  !
  3. Image intitulée Solve Math Problems Step 3
    3
    Reformulez le problème. Certes, ce n'est pas toujours possible, mais quand cela est possible, à voix haute (chez vous) ou sur feuille (en classe) reformulez avec vos propres mots les données du problème en faisant attention à ne pas introduire d'erreurs. Le danger durant cette étape est de mal formuler, aussi réfléchissez bien et relisez scrupuleusement votre reformulation [2] .
  4. Image intitulée Solve Math Problems Step 4
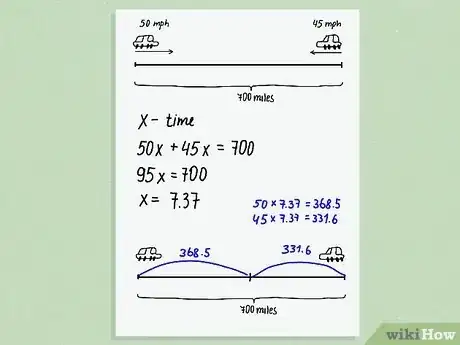
    4
    Faites un schéma. Ce n'est pas toujours possible, mais certains exercices se comprennent mieux (et donc se résolvent mieux !) schéma à l'appui. En fonction des données, vous ferez un schéma plus ou moins élaboré, quelques figures, noterez quelques nombres. Au fil de la progression, n'hésitez pas à refaire le schéma pour aller plus loin. Une fois le schéma fait, vérifiez qu'il correspond bien au problème. Au moindre doute, n'hésitez pas à refaire un schéma plus conforme aux données [3] .
    • Certains exercices se résolvent grâce à un diagramme de Venn. Ce diagramme, très en vogue dans les années 1970 sous le nom de « patates », permet de bien montrer les relations logiques entre plusieurs ensembles d'éléments [4] .
    • Certains exercices nécessitent le recours à un histogramme ou une courbe.
    • Certains exercices demandent la construction d'une ligne, orientée ou non, graduée ou non.
    • En géométrie, dessinez les figures impliquées dans le problème, sans oublier l'échelle et les axes.
  5. Image intitulée Solve Math Problems Step 5
    5
    Trouvez la structure de l'exercice. Pour avoir déjà fait beaucoup d'exercices, une première lecture d'un problème devrait vous aider à classer les informations données et à y associer des savoir-faire. Ici, ce sera un tableau à x colonnes et y lignes, là, une équation qui ressemble à une autre déjà vue, mais en apparence différente. Il ne faut jamais se laisser déstabiliser et toujours se raccrocher à ce que l'on sait faire : la démarche compte finalement plus que le résultat !
  6. Image intitulée Solve Math Problems Step 6
    6
    Vérifiez bien les informations collectées. Il ne s'agirait pas de lire le libellé de travers et de partir sur une mauvaise piste dès le départ. Comparez les notes que vous avez prises et le libellé de l'exercice, voyez si rien ne manque et si tout est juste (nombres, formes géométriques, équations…) Si vous êtes chez vous et que vous ne comprenez pas tout, prenez le temps de vous renseigner dans votre manuel ou sur Internet. Ne cherchez pas cet exercice particulier, mais des exercices similaires pour apprendre les modes de résolution, c'est bien plus formateur et gratifiant !
    Publicité

Partie 2
Partie 2 sur 3:
Établir une méthode de résolution

  1. Image intitulée Solve Math Problems Step 7
    1
    Dressez la liste des formules que vous pensez devoir utiliser. Vous pouvez le faire mentalement ou en les écrivant. En lisant l'énoncé, si une formule ou un savoir-faire particulier (une démonstration, par exemple) vous vient à l'esprit, il serait bon de l'écrire. Cela vaut surtout pour les exercices un peu complexes faisant entrer en jeu divers concepts [5] .
  2. Image intitulée Solve Math Problems Step 8
    2
    Si c'est possible, dressez la liste des étapes de la résolution. Cela suppose de maitriser son sujet. Vous travaillez certes là dans l'absolu, mais cette liste va vous servir de guide tout au long de la résolution. Si votre cerveau sait anticiper, peut-être aurez-vous à la fin de ce travail une idée de la réponse, ce qui sera bien utile quand vous aurez le résultat final [6]  [7] .
  3. Image intitulée Solve Math Problems Step 9
    3
    Exercez-vous sur un problème du même type, mais plus simple. Admettons que vous fassiez un exercice de votre manuel, voyez s'il n'y en a pas un, sur la même page, mais plus simple. Sa résolution sera logiquement plus simple et l'expérience aidant, vous devriez résoudre l'exercice suivant toujours plus compliqué, mais du même type. Il y a des chances que vous ayez à utiliser les mêmes outils mathématiques [8]  [9] .
  4. Image intitulée Solve Math Problems Step 10
    4
    Essayez de deviner la réponse au problème. Ce n'est pas toujours simple et possible dès le départ. Mais dès que vous le pouvez, essayez de penser à la solution possible : on parle ici de « cohérence » de la réponse. Ainsi, pour résoudre une inéquation, vous pourriez très bien à un moment donné vous dire que l'ensemble des solutions ne peut en aucun cas renfermer des nombres négatifs, ce que vous confirmerez par la suite [10] .
    Publicité

Partie 3
Partie 3 sur 3:
Résoudre un problème de mathématiques

  1. Image intitulée Solve Math Problems Step 11
    1
    Ne dérogez pas à votre méthode. Après avoir relu les différentes étapes de la résolution que vous avez cru devoir être les bonnes, passez à leur application. Au terme de chacune d'elles, vérifiez la cohérence et la justesse du résultat.
  2. Image intitulée Solve Math Problems Step 12
    2
    Comparez vos résultats avec vos estimations. À chaque étape résolue, demandez-vous si la réponse est cohérente avec ce que vous croyez savoir de la réponse. Au moindre doute, vérifiez votre raisonnement, vos formules ou vos calculs. Cette méthode de contrôle systématique des résultats des différentes étapes n'est maitrisée qu'au fil du temps, des conseils du professeur, des leçons et des exercices [11] .
  3. Image intitulée Solve Math Problems Step 13
    3
    Essayez une autre méthode. Si la précédente débouchait sur une impasse ou une incohérence, essayez une autre méthode. Une chose est sure : celle-ci ne fonctionne pas, donc il en existe une autre ! En fait, un échec est formateur, la prochaine fois que vous rencontrez une difficulté de ce type vous gagnerez du temps à ne pas utiliser cette méthode. Réfléchissez et trouvez où le raisonnement est faux.
  4. Image intitulée Solve Math Problems Step 14
    4
    Revenez sur le problème. Vous êtes apparemment arrivé(e) à le résoudre, mais il est toujours salutaire de reprendre tout le raisonnement et les calculs pour vérifier que rien ne cloche. Durant cette relecture, chez vous, n'hésitez pas à reviser un point délicat que vous ne maitrisez pas encore parfaitement.
    Publicité

Conseils

  • En vue d'un travail à rendre, n'hésitez pas à faire appel à votre professeur si vous coincez dans le raisonnement ou le calcul. Pour être efficace, cette demande doit être précédée d'un travail sérieux. Le professeur vous donnera non la réponse, mais une piste de résolution.
  • En cas d'exercices difficiles à résoudre, faites le point après leurs résolutions. Révisez sur le livre et dans votre cours la partie théorique et les exercices, c'est ainsi qu'on progresse en mathématiques.
Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  2. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  3. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  4. ↑ https://www.lucidchart.com/pages/fr/diagramme-de-venn
  5. ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
  6. ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
  7. ↑ https://math.berkeley.edu/~gmelvin/polya.pdf
  8. ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
  9. ↑ https://math.berkeley.edu/~gmelvin/polya.pdf
  1. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  2. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies

À propos de ce wikiHow

Daron Cam
Coécrit par:
Daron Cam
Accompagnateur scolaire
Cet article a été coécrit par Daron Cam. Daron Cam est un accompagnateur scolaire et le fondateur de Bay Area Tutors, Inc, un bureau de tutorat situé dans la région de la baie de San Francisco. Il propose un accompagnement en mathématiques, en sciences et d’une manière générale en renforcement de la confiance en soi à l’école. Daron a plus de huit ans d'expérience dans l'enseignement des mathématiques en classe et plus de neuf ans de tutorat individuel. Il enseigne à tous les niveaux de maths, y compris le calcul, la préalgèbre, l'algèbre I, la géométrie et la préparation aux maths SAT/ACT. Daron est titulaire d'une licence de l'université de Californie, Berkeley, et d'un diplôme d'enseignement des mathématiques du St. Mary's College. Cet article a été consulté 11 823 fois.
Catégories: Mathématiques
Publicité