Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 7 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 9 818 fois.
Une inéquation, linéaire comme du second degré, se représente graphiquement (repère orthonormé) comme une équation, à la différence près que l'ensemble des solutions n'est pas une courbe ou une droite, mais une zone du graphe. C'est le signe de l'inégalité qui entraine cette différence : il y a beaucoup plus de solutions avec une inéquation. Il faut commencer par tracer la courbe ou la droite induite par l'équation associée et ensuite déterminer quelle zone est l'ensemble des solutions. Si vous savez déjà tracer le graphe d'une équation, ce ne sera pas compliqué.
Étapes
Méthode 1
Méthode 1 sur 3:Représenter une inéquation linéaire sur une droite graduée
-
1Simplifiez l'inéquation. Pour résoudre une inéquation, il faut parvenir à isoler à gauche la variable et cela se fait de la même façon que pour une équation : toute opération doit être faite sur les deux membres [1] . Pour rappel, un produit ou une division par un nombre négatif entraine l'inversion de l'inéquation.
- Vous avez à résoudre l'inéquation suivante : . Commencez par isoler à gauche l'inconnue et pour cela, vous ajouterez 9 aux deux membres de l'inéquation, après quoi vous diviserez ces deux mêmes membres par 3 :
- Cette méthode de la droite graduée n'est possible que si vous avez une inéquation qu'avec une seule variable ( ou ). Si vous en avez deux ( et ), il faudra utiliser un repère orthonormé, ce qui sera vu plus loin.
- Vous avez à résoudre l'inéquation suivante : . Commencez par isoler à gauche l'inconnue et pour cela, vous ajouterez 9 aux deux membres de l'inéquation, après quoi vous diviserez ces deux mêmes membres par 3 :
-
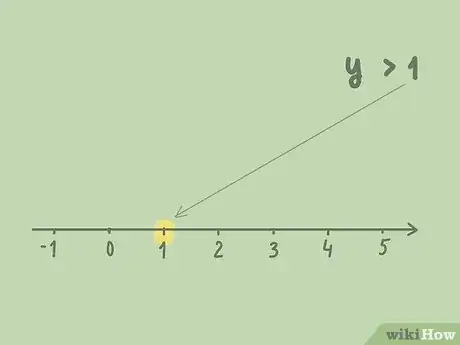
2Tracez une droite graduée. Sur celle-ci, indiquez obligatoirement la valeur limite : avec , 1 est cette valeur. Ensuite, graduez de chaque côté de cette valeur en mettant 4 ou 5 points, plus si vous pouvez. L'intervalle entre les graduations est identique.
- Nous avons donc une inéquation : . Tracez une droite graduée verticale (à cause du ), marquez le 1 et faites quelques graduations comme sur l'illustration.
-
3Tracez un crochet pour marquer la valeur limite. Si l'inéquation est stricte
( ou ), c'est-à-dire que la valeur n'appartient pas à l'ensemble des solutions, alors vous ferez sur la valeur limite un crochet tourné à l'opposé des solutions. Si l'inéquation est large ( ou ), alors la valeur limite appartient aux solutions, et vous ferez sur la valeur limite un crochet tourné en direction des solutions [2] .- Avec , 1 n'appartient pas à l'ensemble des solutions, il faudra donc tracer un crochet exclusif (⸢⸣) qui tourne le dos à l'ensemble des solutions qui sont ici vers le haut.
-
4Tracez la flèche des solutions. Partez de la valeur limite et voyez si la valeur juste supérieure vérifie l'inéquation. Si c'est le cas, alors cette valeur et toutes celles qui lui sont supérieures font partie des solutions : la flèche part de la valeur limite et va à l'infini. Si ce n'est pas le cas, alors ce sont toutes les valeurs inférieures à la valeur limite qui sont solutions ; la flèche est orientée vers le bas [3] .
- Pour , l'ensemble des solutions sera représenté par une flèche orientée vers le haut, ce sont toutes les valeurs supérieures à 1.
Publicité
Méthode 2
Méthode 2 sur 3:Représenter une inéquation linéaire dans un repère
-
1Trouvez . Pour cela, il vous faut, en faisant passer les bons termes d'un côté et de l'autre, isoler le terme en à gauche de l'inéquation [4] . En conséquence, le terme en sera dans le membre de droite, ainsi que la constante, s'il y en a une.
- Prenons comme exemple l'inéquation . L'isolement de se fait en deux étapes, d'abord vous soustrayez 9 des deux côtés, puis vous divisez, toujours des deux côtés, par 3 :
- Prenons comme exemple l'inéquation . L'isolement de se fait en deux étapes, d'abord vous soustrayez 9 des deux côtés, puis vous divisez, toujours des deux côtés, par 3 :
-
2Tracez la courbe dans un repère orthonormé. Vous avez une inéquation, mais pour la résoudre, vous devez la transformer en une équation en changeant le symbole > en =. Ainsi, vous pourrez tracer le graphe de cette fonction [5] . Pour tracer une droite affine, il suffit d'avoir deux points, ceux que vous voulez.
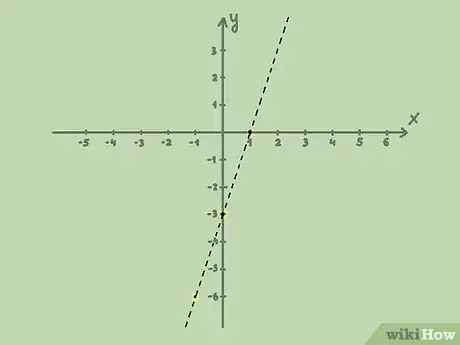
- Repartons de l'inéquation . Vous allez tracer la droite d'équation . Tracez deux points de cette droite. Prenons, par exemple, le point d'abscisse 1, son image () est 0 () : marquez le point P1 (1,0). Prenons un second point, celui ayant pour abscisse - 1, son image () est - 6
() : le deuxième point est P2 (- 1,- 6).
- Repartons de l'inéquation . Vous allez tracer la droite d'équation . Tracez deux points de cette droite. Prenons, par exemple, le point d'abscisse 1, son image () est 0 () : marquez le point P1 (1,0). Prenons un second point, celui ayant pour abscisse - 1, son image () est - 6
-
3Tracez la courbe. Si l'inéquation est stricte (symbole ( ou ), vous tracerez la droite en pointillés, marquant par là que la droite ne fait pas partie des solutions. Par contre, si l'inéquation est large (symbole ( ou ), la courbe sera tracée en trait plein, signifiant par là qu'elle fait partie des solutions [6] .
- Reprenons notre exemple, l'inéquation . L'l'inéquation est stricte : le tracé de la courbe est en pointillés, elle ne fait pas partie des solutions.
-
4Hachurez ou ombrez l'ensemble des solutions. Pour hachurer la bonne zone, prenez un point quelconque et voyez si l'inégalité est vérifiée. Si c'est le cas, alors toute la zone où il se trouve est l'ensemble des solutions, sinon c'est la zone de l'autre côté de la droite [7] .
- Reprenons notre inéquation et voyons si le point (-3,0), à gauche de la courbe, est dans l'ensemble des solutions. Calculez , soit
. l'inégalité est juste, donc hachurez toute la zone à gauche de la droite.
Publicité - Reprenons notre inéquation et voyons si le point (-3,0), à gauche de la courbe, est dans l'ensemble des solutions. Calculez , soit
Méthode 3
Méthode 3 sur 3:Représenter une inéquation du second degré dans un repère
-
1Vérifiez que vous avez bien affaire à une inéquation du second degré. Un des membres de votre inéquation doit être de la forme [8] . Si le terme en ou la constante () sont absents, cela reste une expression du second degré tant qu'il y a un terme en dans un membre et dans l'autre.
- Prenons comme exemple la représentation graphique de l'inéquation
.
- Prenons comme exemple la représentation graphique de l'inéquation
-
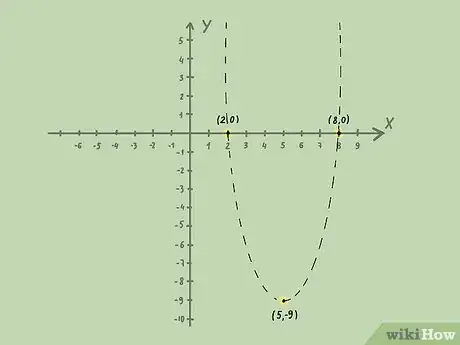
2Tracez la courbe dans un repère orthonormé. Tracez la courbe de l'équation dérivée de l'inéquation, à savoir . comme c'est une équation du second degré, il y a de grandes chances que la courbe soit une parabole [9] .
- Admettons que vous deviez résoudre graphiquement l'inéquation
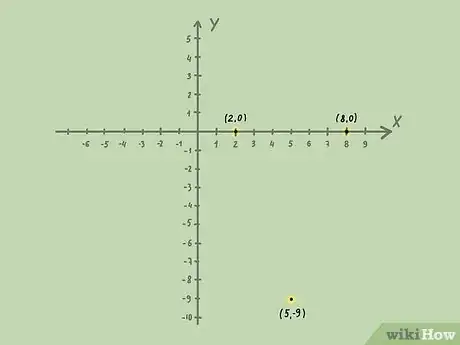
. Commencez par tracer la courbe . Le sommet de la parabole est en , et la parabole coupe l'axe des abscisses en deux points : et .
- Admettons que vous deviez résoudre graphiquement l'inéquation
-
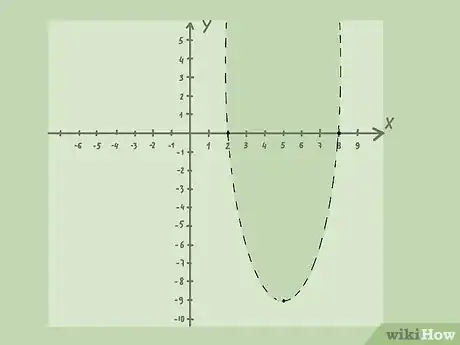
3Tracez la parabole. Si l'inéquation est stricte (symbole ( ou ), vous tracerez la parabole en pointillés, marquant par là que la droite ne fait pas partie des solutions. Par contre, si l'inéquation est large (symbole ( ou ), la parabole sera tracée en trait plein, signifiant par là qu'elle fait partie des solutions.
- Dans notre exemple, , la parabole doit être tracée en traits pointillés, car l'inéquation est stricte.
-
4Aidez-vous de certains points. Pour savoir quelle zone vous devez hachurer, prenez un point où vous voulez, soit à l'intérieur de la parabole, soit à l'extérieur.
- Reprenons notre inéquation . Pour des raisons pratiques de calcul, nous testerons le point (0,0), lequel est à l'extérieur de la parabole. Rien n'empêche de prendre un point à l'intérieur !
-
5Hachurez ou grisez l'ensemble des solutions. Cet ensemble est une aire et avec une parabole, il y en a deux, celle à l'intérieur de la parabole et celle à l'extérieur. Pour hachurer la bonne zone, prenez un point quelconque et voyez si l'inégalité est vérifiée. Si c'est le cas, alors toute la zone où il se trouve est l'ensemble des solutions, sinon c'est la zone de l'autre côté de la droite [10] .
- Nous avons choisi de prendre le point origine (0,0), à l'extérieur de la parabole. Calculez ainsi :
L'inégalité étant juste, vous pouvez donc en conclure que toute la zone située en dehors de la parabole représente l'ensemble des solutions. C'est simple, non !
Publicité - Nous avons choisi de prendre le point origine (0,0), à l'extérieur de la parabole. Calculez ainsi :
Conseils
- Avant de représenter graphiquement une inéquation, il faut toujours la simplifier si c'est possible !
- Si vraiment vous ne parvenez pas à trouver la solution graphique, prenez une calculatrice graphique et tapez l'inéquation, puis validez.
Références
- ↑ http://www.virtualnerd.com/algebra-2/equations-inequalities/linear-inequalities/solve-multi-step-inequalities/inequality-two-step-solution-and-graph
- ↑ https://www.youtube.com/watch?v=8vOkpZr8x0w
- ↑ http://www.purplemath.com/modules/ineqlin.htm
- ↑ http://www.mathsisfun.com/algebra/graphing-linear-inequalities.html
- ↑ http://www.mathsisfun.com/algebra/graphing-linear-inequalities.html
- ↑ http://www.purplemath.com/modules/ineqgrph.htm
- ↑ http://www.mathsisfun.com/algebra/graphing-linear-inequalities.html
- ↑ https://www.mathsisfun.com/algebra/inequality-quadratic-solving.html
- ↑ http://www.virtualnerd.com/algebra-2/quadratics/inequalities/graphing-solving-inequalities/graph-inequality



























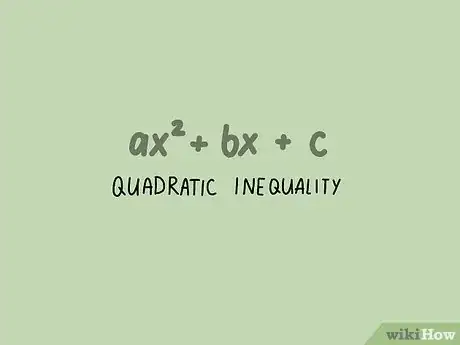































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 9 818 fois.