Comment retenir les divisions du cercle trigonométrique

Coécrit par l'équipe de wikiHow

Si vous étudiez les fonctions trigonométriques, bien connaitre le cercle trigonométrique et ses différentes divisions est bien sûr un passage obligé, mais cela pourra aussi vous aider en géométrie ou même en calcul algébrique. Au premier abord, apprendre ces divisions semble compliqué, mais quand vous aurez compris comment on les obtient, vous verrez que c'est un apprentissage somme toute facile. Il vaut mieux comprendre ce cercle plutôt que l'apprendre par cœur.

Partie 1

Partie 1 sur 2:
Retenir des valeurs en radians d'un cercle

1
Tracez deux lignes perpendiculaires. Sur une feuille de papier, tracez deux lignes, l’une horizontale et l’autre, verticale se croisant à angle droit au milieu de votre feuille. Ce seront les deux axes, respectivement des abscisses (« x ») et des ordonnées (« y »).
2
Tracez un cercle. À l'aide d'un compas, tracez un grand cercle dont le centre sera le point d'intersection des deux lignes.
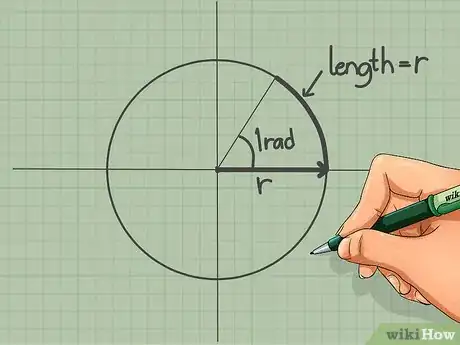
3
Comprenez bien ce que sont les radians. Le radian est une unité de mesure des angles. Pour prendre une image, une personne qui marcherait sur la circonférence d'un cercle d'un rayon d'une unité et parcourrait une distance d'une unité aurait parcouru l'arc d'un secteur angulaire d'un radian. Dans l'étape suivante, nous découperons le cercle en quatre parties égales, avec pour chacune sa valeur en radians. Retenez ce rapport de longueur qui existe entre le rayon et un arc de cercle.
- Par convention, la mesure des radians commence toujours au point de coordonnées (1,0). Pour que les explications soient plus claires, nous allons imaginer que le cercle est une rose des vents.
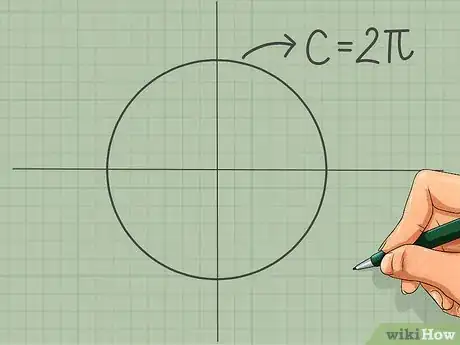
4
Sachez qu’un cercle complet représente un angle de 2π radians. La circonférence d'un cercle est égale à 2πr, r étant le rayon du cercle : un cercle d'un rayon d'un mètre a une circonférence de 2π m. Pour trouver la mesure d'un angle en radians d'un point du cercle, divisez 2π par le pourcentage de longueur de circonférence depuis un point origine. Il est inutile de dire qu'il impossible de retenir la valeur en radians de chaque point du cercle.
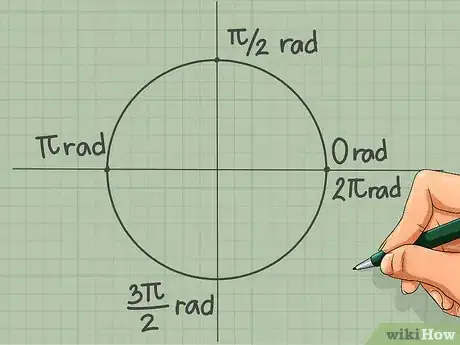
5
Inscrivez la valeur en radians des quatre points d'intersection. Votre cercle est divisé en quatre quartiers égaux. Les points d'intersection sont ceux du cercle avec les deux axes
- « Est » est notre point origine, il vaut 0 rad.
- « Nord » représente un quart de la circonférence et vaut donc : ^2π/₄ = ^π/₂ radians.
- « Ouest » représente une moitié de la circonférence et vaut : ^2π/₂ = π radians.
- « Sud » représente les trois quarts de la circonférence et vaut : ¾ x 2π = ^3π/₂ radians.
- Après un tour complet, vous revenez au point de départ. L’angle parcouru est alors de 2π rad, c’était aussi votre point 0 rad.
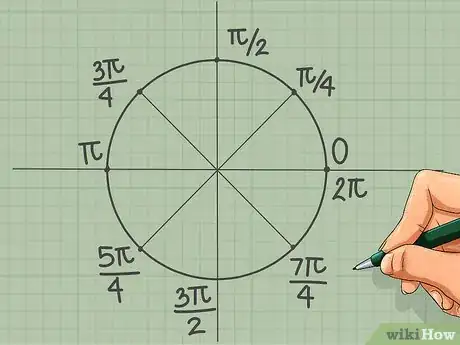
6
Divisez un cercle en huit parts égales. Tracez deux lignes qui partagent en deux chacun des quatre quadrants. Pour trouver la valeur en radians de ces points spécifiques, il faut utiliser la division :
- ^π/₄
- ^3π/₄
- ^5π/₄
- ^7π/₄
- (0, π/2, π, 3π/2 et 2π sont déjà mentionnés).
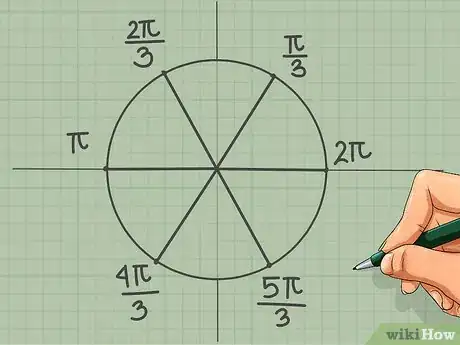
7
Divisez un cercle en six parts égales. Prenez un rapporteur, partez du point origine (0 rad) et faites des marques tous les 60° (^2π/₆ = ^π/₃). Tracez les rayons à partir de ces marques. Plus simple, vous tracez le trait horizontal (de 0 à π radians), puis les marques 60° et 120° et vous tracez les diamètres depuis ces marques. Les points d'intersection (un par quadrant) avec le cercle sont les suivants :
- ^π/₃
- ^2π/₃
- ^4π/₃
- ^5π/₃
- (π et 2π sont déjà mentionnés)
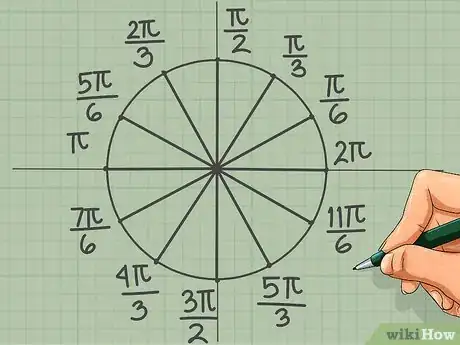
8
Divisez un cercle en douze parts égales. À partir du cercle précédent, divisez chaque segment en deux parts égales. Seuls quatre de ces points n'ont pas encore de valeur, ce sont :
- ^π/₆
- ^5π/₆
- ^7π/₆
- ^11π/₆
Publicité

Partie 2

Partie 2 sur 2:
Bien mémoriser les coordonnées (cosinus, sinus)

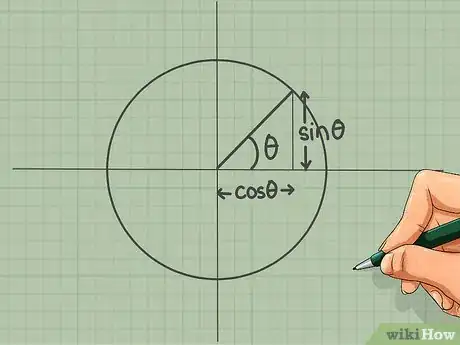
1
Comprenez bien ce que sont le cosinus et le sinus. Le cercle trigonométrique est particulièrement utile dans les problèmes impliquant des angles droits. θ étant la mesure de l’angle, l’abscisse d’un point du cercle est le cosinus de cet angle, tandis que l’ordonnée est le sinus de ce même angle.
- Pour mieux retenir, imaginez que tout point d'un cercle a pour coordonnées (cos(θ), sin(θ)).
- Avec un triangle rectangle, vous pouvez retenir les trois principales fonctions trigonométriques en pensant au mot baroque : sohcahtoa (soh pour sin(θ) = côté opposé sur hypothénuse).
2
Inscrivez les quatre principaux points du cercle. Un cercle trigonométrique est un cercle théorique qui a pour rayon une unité de longueur. Cela simplifie les choses quand il s'agit de donner les coordonnées (x,y) des quatre points d'intersection des deux axes et du cercle. Pour des raisons de commodité, nous reprendrons les appellations Est, Ouest, Nord et Sud, mais ce ne sont pas là des dénominations officielles.
- Les coordonnées d'Est sont (1, 0).
- Les coordonnées de Nord sont (0, 1).
- Les coordonnées d'Ouest sont (-1, 0).
- Les coordonnées de Sud sont (0, -1).
- Comme vous le voyez, cela fonctionne comme un simple repère orthonormé. Si vous savez opérer avec un tel repère, vous saurez retrouver facilement les coordonnées de ces quatre points.
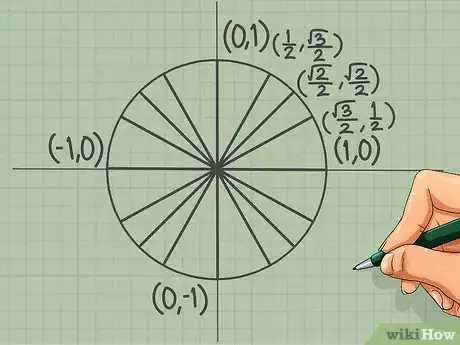
3
Retenez certaines coordonnées du premier quadrant. Il s'agit donc du quart supérieur droit du cercle dans lequel les coordonnées de tous les points sont positives. Vous avez à en retenir trois :
- pour ^π/₆, les coordonnées sont ( ${\frac {\sqrt {3}}{2}},{\frac {1}{2}}$ )
- pour ^π/₄, les coordonnées sont ( ${\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}$ )
- pour ^π/₃, les coordonnées sont ( ${\frac {1}{2}},{\frac {\sqrt {3}}{2}}$ )
- notez qu'il n'y a que trois numérateurs possibles. Si vous progressez en sens positif (de la gauche vers la droite pour les abscisses, du bas vers le haut pour les ordonnées), les coordonnées respectives vont dans le sens : 1 → √2 → √3
4
Tracez des diamètres pour trouver d'autres coordonnées. Deux points opposés d'un cercle, reliés donc par une même ligne, ont les mêmes coordonnées (x, y) en valeurs absolues. Dit autrement, si vous tracez un diamètre depuis un point du premier quadrant, le point opposé, dans le troisième quadrant a les mêmes coordonnées aux signes près.
- Ainsi, vous pouvez tracer une ligne horizontale entre ^π/₃ et ^2π/₃. Les coordonnées du premier point étant ( ${\frac {1}{2}},{\frac {\sqrt {3}}{2}}$ ), celles du second sont : (? ${\frac {1}{2}},?{\frac {\sqrt {3}}{2}}$ ), le "?" est là pour indiquer le signe « + » ou « - ».
- Remarquez certains points particuliers du cercle trigonométrique. Tous les points ayant une ordonnée du genre ${\frac {x}{3}}$ ont la même abscisse, en valeur absolue bien sûr. Il en va de même des points ayant une ordonnée en ${\frac {x}{4}}$ ou ${\frac {x}{6}}$ .
5
Utilisez la symétrie pour déterminer les signes. La détermination des signes des abscisses et des ordonnées des points d'un cercle trigonométrique n'est pas si difficile que cela, il y a plusieurs moyens de les retenir.
- Ce qui est vrai pour tout point d'un repère orthonormé est vrai pour un cercle trigonométrique. Tout point du cercle au-dessus de l’axe des « x » a une ordonnée positive, au-dessus, elle est négative. Tout point du cercle situé à droite de l’axe des ordonnées (« y ») a une abscisse positive et négative s’il est à gauche.
- Imaginons que vous partiez d'un point du cercle dans le premier quadrant et que vous traciez des lignes dans tous les sens depuis ce point. Si la ligne coupe l'axe des « y », l’ordonnée (« y ») du point d'arrivée change de signe. Si elle coupe l'axe des « x », c’est cette fois-ci l’abscisse (« x ») qui change de signe.
- Retenez ce mot mnémotechnique « toussitaco ». En se déplaçant dans le sens contraire des aiguilles d'une montre, dans le premier quadrant, les points ont tous des coordonnées positives, dans le deuxième, seuls les sinus sont positifs, dans le troisième, seules les tangentes le sont et dans le quatrième, seuls les cosinus le sont.
- Quelle que soit la méthode choisie, les signes des points sont (+,+) pour le premier quadrant, (-,+) pour le deuxième quadrant, (-,-) pour le troisième quadrant et (+,-) pour le dernier quadrant.
6
Vérifiez vos calculs. Vous trouverez ci-dessous, en sens contraire des aiguilles d'une montre, tous les points d'un cercle trigonométrique (hormis les points d'intersection avec les axes) Pour tous les retenir, il suffit de mémoriser les seuls points du premier quadrant :
- quadrant 1 : ( ${\frac {\sqrt {3}}{2}},{\frac {1}{2}}$ ) - ( ${\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}$ ) - ( ${\frac {1}{2}},{\frac {\sqrt {3}}{2}}$ )
- quadrant 2 : ( $-{\frac {1}{2}},{\frac {\sqrt {3}}{2}}$ ) - ( $-{\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}$ ) - ( $-{\frac {\sqrt {3}}{2}},{\frac {1}{2}}$ )
- quadrant 3 : ( $-{\frac {\sqrt {3}}{2}},-{\frac {1}{2}}$ ) - ( $-{\frac {\sqrt {2}}{2}},-{\frac {\sqrt {2}}{2}}$ ) - ( $-{\frac {1}{2}},-{\frac {\sqrt {3}}{2}}$ )
- quadrant 4 : ( ${\frac {1}{2}},-{\frac {\sqrt {3}}{2}}$ ) - ( ${\frac {\sqrt {2}}{2}},-{\frac {\sqrt {2}}{2}}$ ) - ( ${\frac {\sqrt {3}}{2}},-{\frac {1}{2}}$ )
Publicité

Conseils

Si vous avez de nombreux exercices sur des cercles, le mieux est de tracer un cercle théorique au brouillon, lequel vous servira de référence tout au long des questions à résoudre.
Cela peut paraitre un peu long au départ, mais avec de l’entrainement, vous irez très vite. Avec de la pratique, il vous suffira de regarder les deux axes, vous n'aurez plus besoin d'avoir le cercle trigonométrique théorique sous les yeux.