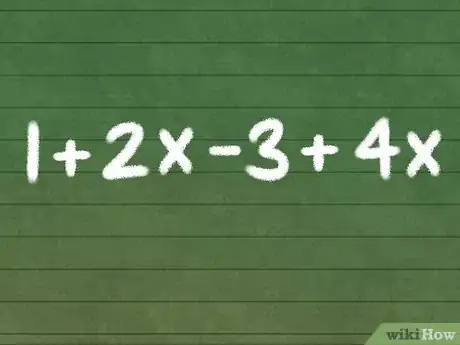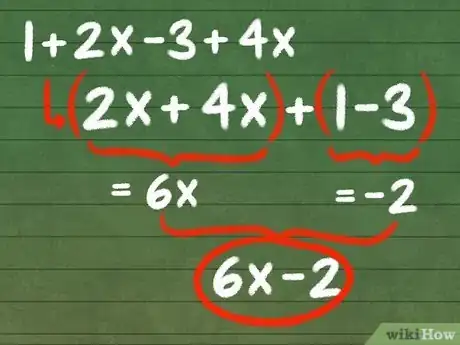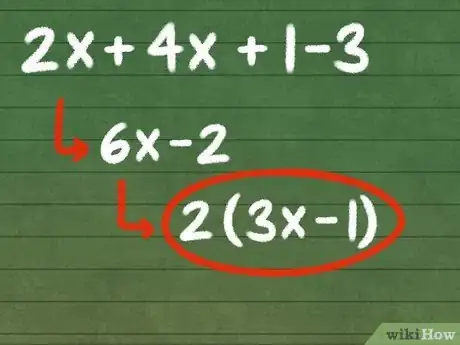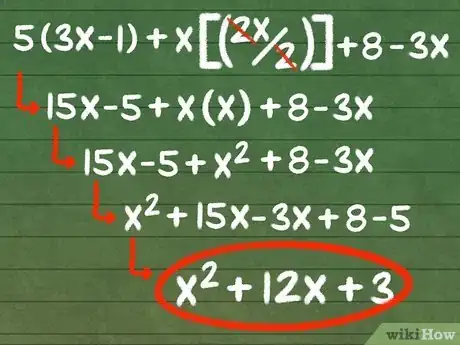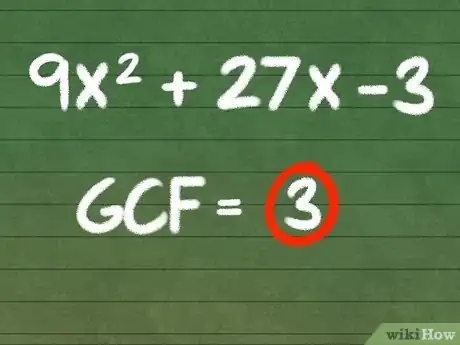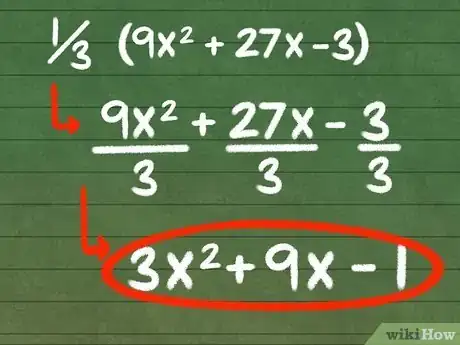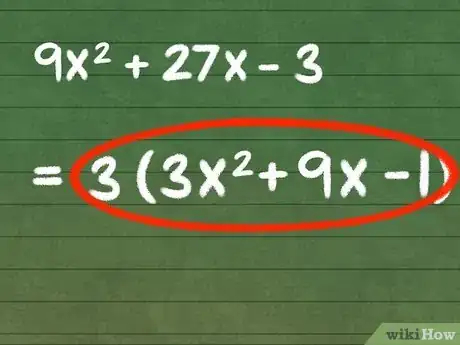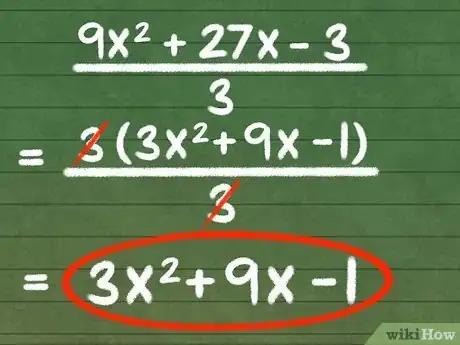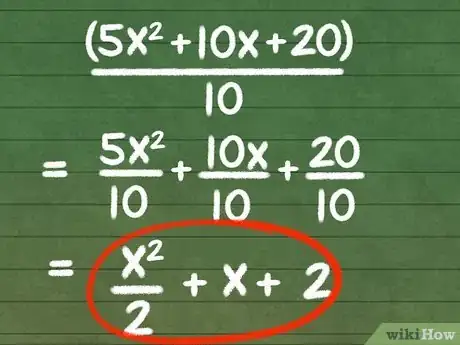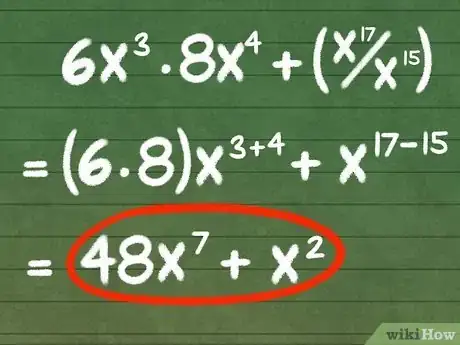Comment simplifier les expressions algébriques

Informations concernant l'auteur.e

Pour maitriser l’algèbre, il est nécessaire de savoir comment simplifier les expressions algébriques. Il s’agit d’une technique élémentaire que tout mathématicien doit maitriser, car elle permet de transformer une expression compliquée, longue et embarrassante en quelque chose de plus élégant et de plus facile à manier. Il n’est pas difficile d’apprendre les méthodes élémentaires de simplification, même pour quelqu’un qui n’est pas doué pour les mathématiques. Lisez les étapes suivantes pour apprendre à simplifier la plupart des expressions algébriques courantes, même si vous n’avez pas des connaissances approfondies en mathématiques.

Méthode 1

Méthode 1 sur 4:
Se familiariser avec les concepts importants

1
Définissez les termes semblables suivant leurs variables et leurs puissances. En algèbre, les « termes semblables » sont composés des mêmes variables affectées des mêmes exposants. Autrement dit, deux termes sont « semblables » lorsqu’ils contiennent la même ou les mêmes variables ou aucune variable et que toutes les variables sont affectées d’un même exposant ou n’ont pas d’exposant du tout. La distribution des variables dans les expressions en question importe peu.
- Par exemple, 3x² et 4x² sont deux termes semblables, car chacun d’eux contient la variable x élevée au carré. Cependant, x et x² ne sont pas deux termes semblables, car dans chaque terme la variable x est élevée à une puissance différente. De même - 3yx et 5xz ne sont pas deux termes semblables, car chacun contient un couple différent de variables.
2
Factorisez en écrivant les nombres sous la forme d’un produit de deux facteurs. La factorisation consiste à représenter un nombre donné sous la forme d’une multiplication de deux facteurs. Un nombre peut être décomposé en plusieurs facteurs, par exemple le nombre 12 peut s’écrire sous la forme : 1 × 12, 2 × 6 et 3 × 4. Ainsi vous pouvez dire que 1, 2, 3, 4, 6 et 12 sont des facteurs de 12. Une autre manière de présenter cette question consiste à dire que ces facteurs correspondent aux nombres par lesquels le nombre considéré est divisible.
- Par exemple, si vous voulez factoriser le nombre 20, vous pouvez l’écrire sous la forme 4 × 5.
- Notez que les termes contenant des variables peuvent également être factorisés. Par exemple, le terme 20x peut s’écrire sous la forme 4(5x).
- Les nombres premiers ne sont pas factorisables parce qu’ils ne sont divisibles que par eux-mêmes et par 1.
3
Souvenez-vous de l’acronyme PEMDAS pour ne pas oublier l’ordre des opérations. Souvent, la simplification d’une expression se limite à l’organiser et à faire des opérations afin de réduire l’expression à sa forme la plus simple. Si c’est le cas, souvenez-vous l’ordre des opérations pour ne pas faire d’erreurs. L’acronyme PEMDAS peut vous aider à vous souvenir de cet ordre. Les lettres correspondent aux opérations successives que vous devez faire :
- Parenthèses
- Exposants
- Multiplication
- Division
- Addition
- Soustraction
Publicité

Méthode 2

Méthode 2 sur 4:
Combiner les termes semblables

1
Écrivez votre équation. Souvent, vous pouvez résoudre en quelques étapes faciles les équations algébriques les plus simples, c’est-à-dire celles qui ne contiennent que quelques variables ayant des coefficients composés d’un nombre entier, sans radicaux ou fractions, etc. Comme pour la majorité des problèmes de mathématiques, l’étape initiale de la simplification de votre équation consiste à l’écrire !
- À titre d’exemple pour les étapes suivantes, considérez l’expression 1 + 2x - 3 + 4x.
2
Identifiez les termes semblables. Cherchez les termes semblables dans votre équation. Souvenez-vous que les termes semblables ont la même ou les mêmes variables et les mêmes exposants.
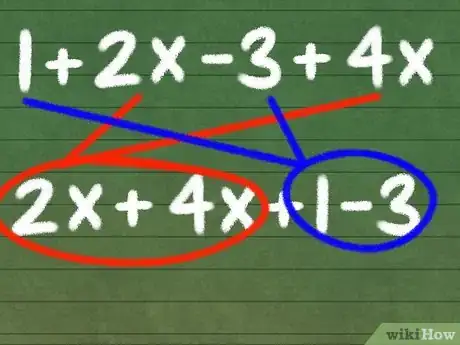
- Par exemple, essayez d’identifier les termes semblables de l’équation : 1 + 2x - 3 + 4x. Notez que 2x et 4x contiennent la même variable affectée du même exposant. Dans ce cas, il s’agit de la variable x qui n’est élevée à aucune puissance. De plus, 1 et - 3 sont des termes semblables, car ils ne contiennent pas de variables. Donc, dans cette équation 2x et 4x ainsi que 1 et - 3 sont des termes semblables.
3
Combinez les termes semblables. À présent que vous avez identifié les termes semblables, vous pouvez simplifier votre équation en les combinant. Réduisez à un seul terme chaque ensemble de termes contenant la même variable et le même exposant en les additionnant ou en les soustrayant si les termes sont négatifs.
- Additionnez les termes semblables de l’exemple précédent.
  - 2x + 4x = 6x
  - 1 + (–3) = - 2
4
Écrivez l’équation simplifiée en utilisant les termes que vous venez d’obtenir. Combinez les termes semblables, ensuite écrivez une nouvelle expression en utilisant les termes simplifiés que vous avez obtenus. Vous devez aboutir à une expression qui contient un terme de chaque ensemble de variables et d’exposants qui forment l’expression initiale. Cette nouvelle expression est équivalente à la première.
- Dans l’exemple précédent, les termes simplifiés sont 6x et - 2, ainsi vous pourrez écrire la nouvelle expression sous la forme : 6x - 2. Cette expression simplifiée est égale à l’expression initiale (1 + 2x - 3 + 4x), sauf qu’elle est plus compacte et plus facile à manier. Elle est aussi plus simple à factoriser, ce qui représente un avantage, car comme vous le verrez ci-dessous, la factorisation fait partie des méthodes de simplification.
5
Respectez l’ordre des opérations lorsque vous combinez les termes semblables. Il est simple d’identifier les termes semblables, en particulier lorsque l’expression est facile comme celle qui a été examinée plus haut. Cependant, dans les expressions plus complexes, comme celles qui contiennent des variables entre parenthèses, des fractions et des radicaux, vous pourrez ne pas repérer immédiatement les termes semblables à combiner. Dans ce cas, suivez l’ordre des opérations et effectuez vos calculs sur les termes de l’expression considérée autant de fois que nécessaire. À la fin, il ne doit vous rester que des additions et des soustractions à faire.
- Par exemple soit l’équation 5(3x - 1) + x[(2x)/(2)] + 8 - 3x. Il est incorrect de considérer d’emblée que 3x et 2x sont des termes semblables et de les combiner, car vous êtes supposé faire des calculs préalables, étant donné que l’expression contient des parenthèses. D’abord, suivez l’ordre des opérations et faites les calculs d’arithmétique dans l’expression pour obtenir des termes que vous pouvez employer. Procédez comme suit :
  - 5(3x - 1) + x[(2x)/(2)] + 8 - 3x
  - 15x - 5 + x(x) + 8 - 3x
  - 15x - 5 + x² + 8 - 3x. À présent, vous pouvez combiner les termes semblables, car les opérations restantes consistent en des additions et des soustractions.
  - x² + (15x – 3x) + (8 - 5)
  - x² + 12x + 3
Publicité

Méthode 3

Méthode 3 sur 4:
Factoriser

1
Identifiez le plus grand commun diviseur dans votre expression algébrique. La factorisation est une méthode pour simplifier les expressions algébriques en supprimant les facteurs communs aux termes de l’expression. Commencez par trouver le plus grand commun diviseur à tous les termes de l’expression. En d’autres termes, il s’agit de trouver le plus grand nombre entier qui divise simultanément tous les termes de l’expression.
- Soit l’équation 9x² + 27x - 3. Notez que chaque terme de l’expression est divisible par 3. Étant donné que les termes de l’expression ne sont pas divisibles par un nombre plus grand que 3, vous pouvez conclure que le plus grand commun diviseur des termes de l’expression est égal à 3.
2
Divisez les termes de l’expression par le plus grand commun diviseur. Divisez chaque terme de l’équation par le plus grand commun diviseur que vous avez identifié. Les termes obtenus auront des coefficients plus petits que ceux de l’équation initiale.
- Factorisez votre équation en employant son plus grand commun diviseur, c’est-à-dire 3. À cette fin, divisez chaque terme par 3.
  - 9x²/3 = 3x²
  - 27x/3 = 9x
  - -3 = -1
  - Ainsi, votre nouvelle expression peut s’écrire sous la forme : 3x² + 9x - 1.
3
Remarquez que la nouvelle expression correspond au produit du plus grand commun diviseur par les termes restants. Votre nouvelle expression n’est pas égale à l’expression initiale et il est donc incorrect de dire que cette dernière a été simplifiée. Pour égaliser la nouvelle expression avec l’expression initiale, vous devez compenser la division par le plus grand commun diviseur que vous avez fait. Pour ce faire, mettez votre expression entre parenthèses et affectez-lui un coefficient de valeur égale à celle du plus grand commun diviseur.
- Pour l’exemple ci-dessus, 3x² + 9x - 1, vous pouvez mettre l’expression entre parenthèses et la multiplier par le plus grand commun diviseur de l’équation initiale afin d’obtenir l’expression suivante : 3(3x² + 9x - 1). Cette dernière équation est égale à l’expression initiale : 9x² + 27x - 3.
4
Simplifiez l’expression en factorisant. À présent, vous commencez à comprendre à quel point la factorisation est utile. Après avoir simplifié votre expression par le plus grand commun diviseur, vous devez multiplier l’expression obtenue par ce même nombre pour obtenir le résultat final. En réalité, la factorisation permet au mathématicien de réaliser plusieurs acrobaties pour simplifier une expression donnée. Une démarche très facile consiste à obtenir une fraction équivalente en multipliant le numérateur et le dénominateur d’une fraction par un même nombre. Lisez les paragraphes suivants pour avoir plus de précisions.
- Supposez que l’expression initiale de l’exemple précédent : 9x² + 27x - 3 forme le numérateur d’une fraction dont le dénominateur est égal à 3. Cette fraction aura la forme suivante : (9x² + 27x - 3)/3. Vous pouvez simplifier cette fraction en la factorisant.
  - Remplacez le numérateur par la forme simplifiée de l’expression initiale : [3(3x² + 9x - 1)]/3
  - Notez qu’à présent le numérateur et le dénominateur contiennent le coefficient 3. En divisant le numérateur et le dénominateur par 3, vous obtenez : (3x² + 9x - 1)/1.
  - Étant donné qu’une fraction est égale à son numérateur lorsque son dénominateur est égal à « 1 », vous pouvez affirmer que la fraction initiale peut s’écrire sous la forme simplifiée suivante : 3x² + 9x - 1.
Publicité

Méthode 4

Méthode 4 sur 4:
Appliquer d’autres méthodes de simplification

1
Simplifiez une fraction en divisant par des facteurs communs. Comme il a été dit plus haut, si le numérateur et le dénominateur d’une expression ont des facteurs communs, ces facteurs peuvent servir à simplifier cette expression. Quelquefois, il est nécessaire de factoriser le numérateur ou le dénominateur ou les deux, comme ce fut le cas dans l’exemple précédent. Parfois, les facteurs communs sont directement identifiables. Notez qu’il est également possible de simplifier l’expression en question en divisant chaque terme du numérateur par le dénominateur.
- Essayez de traiter l’exemple suivant qui ne demande pas une factorisation laborieuse. Soit la fraction (5x² + 10x + 20)/10. Pour la simplifier, vous pouvez diviser chaque terme du numérateur par le dénominateur 10, même si le coefficient « 5 » du terme 5x² est inférieur à 10 et ne peut donc pas admettre ce nombre comme facteur.
  - Une fois votre calcul terminé, vous obtiendrez l’expression suivante : [(5x²)/10] + x + 2. Si vous voulez, écrivez le premier terme sous la forme : (1/2)x² pour obtenir (1/2)x² + x + 2.
2
Utilisez les carrés des nombres pour simplifier les radicaux. On appelle radicande une expression mathématique placée sous un radical. Vous pouvez simplifier une telle expression en identifiant les termes sous forme de carrés qui sont eux-mêmes des nombres entiers élevés au carré et en calculant la racine carrée de chaque terme, afin de l’extraire du radical.
- Soit l’exemple suivant : √(90). Notez que le nombre 90 correspond au produit des deux facteurs 9 et 10 de ce nombre. Par conséquent, vous pouvez extraire la racine carrée de 9 et obtenir le nombre entier 3 et donc le sortir du radical. Autrement dit :
  - √(90)
  - √(9 × 10)
  - [√(9) × √(10)]
  - 3 × √(10)
  - 3√(10)
3
Lorsque vous multipliez deux puissances, additionnez les exposants et retranchez-les quand vous faites une division. Quelques expressions algébriques nécessitent la multiplication ou la division de puissances. Au lieu de calculer chaque puissance et ensuite multiplier ou diviser manuellement, gagnez du temps et additionnez les exposants quand vous multipliez et retranchez-les lorsque vous divisez. Cette méthode permet également de simplifier les expressions qui contiennent des variables.
- Par exemple soit l’expression suivante : 6x³ × 8x⁴ + (x¹⁷/x¹⁵). Chaque fois que vous devez multiplier ou diviser des puissances, additionnez ou faites la différence des exposants, selon le cas, pour trouver l’expression simplifiée plus facilement. Regardez ci-après :
  - 6x³ × 8x⁴ + (x¹⁷/x¹⁵)
  - (6 × 8)x^{3 + 4} + (x^{17 - 15})
  - 48x⁷ + x²
- Ci-après l’explication de ce calcul :
  - La multiplication des puissances est analogue à la multiplication de longues suites de termes qui ne sont pas soumis à une puissance. Par exemple, x³ = (x) × (x) × (x) et x⁵ = (x) × (x) × (x) × (x) × (x), x³ × x⁵ = (x) × (x)× (x) × (x) × (x) × (x) × (x) × (x) ou x⁸.
  - De même, la division des puissances est analogue à la division de longues suites de termes qui ne sont pas soumis à une puissance. Par exemple, x⁵/x³ =[(x) × (x) × (x) × (x) × (x)]/[(x) × (x) × (x)]. Sachant que vous pouvez simplifier le numérateur et le dénominateur en supprimant les facteurs communs, vous n’aurez plus que deux termes en x au numérateur et aucun au dénominateur, ce qui vous donne une réponse égale à x²
Publicité

Conseils

La simplification des expressions algébriques n’est pas une opération simple, mais une fois que vous avez bien compris la technique, vous pourrez l’employer pendant toute votre vie.
Souvenez-vous de tenir compte du signe positif ou négatif du terme sur lequel vous opérez. Plusieurs élèves se trouvent coincés lorsqu’ils se demandent : « Mais quel signe dois-je placer ici ? »
Au besoin, n’hésitez pas à demander de l’aide !

Avertissements

Veillez à ne pas additionner des nombres ou des exposants en trop et assurez-vous de ne pas faire des opérations erronées.
Cherchez toujours les termes semblables et ne vous laissez pas induire en erreur par les exposants.