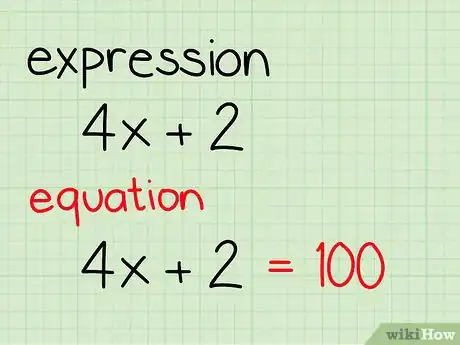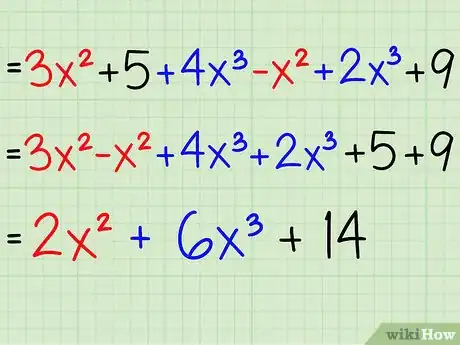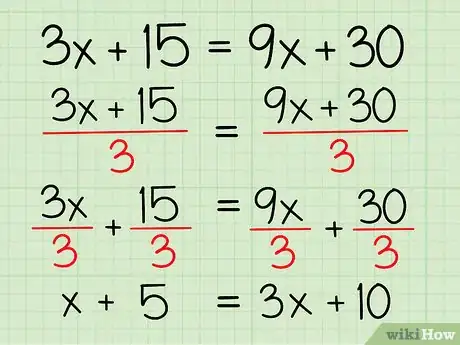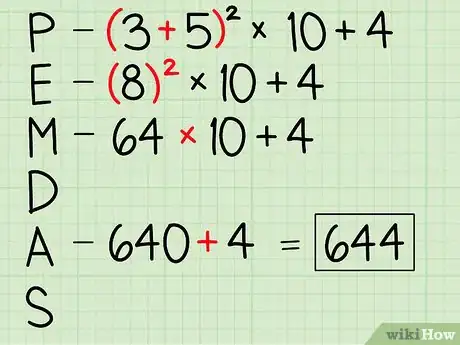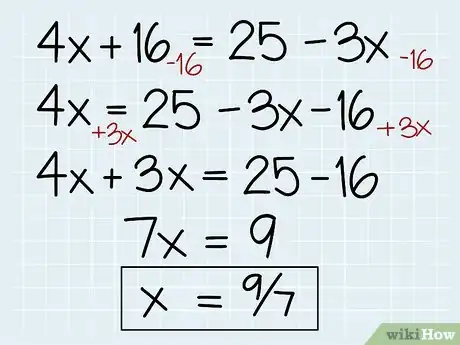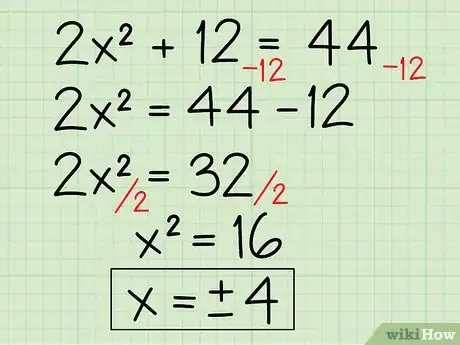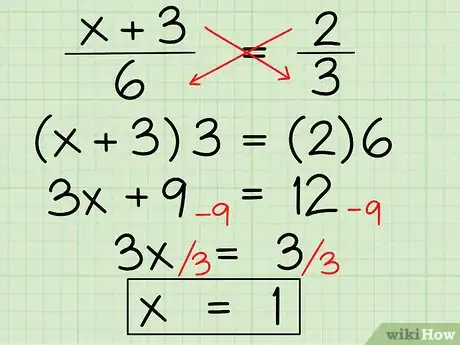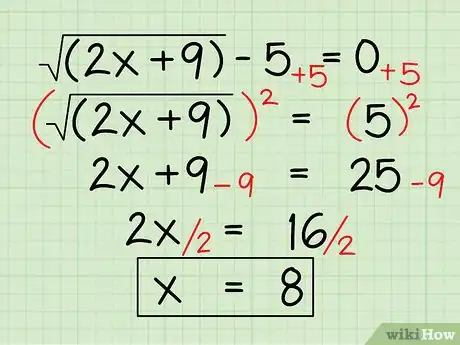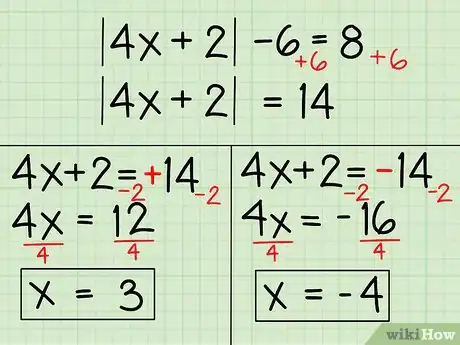Comment simplifier une expression algébrique

Informations concernant l'auteur.e

Une expression algébrique est un ensemble de nombres, de variables et d’opérateurs. Bien qu’il est impossible de résoudre une expression algébrique (car elle ne contient pas de signe), =) il est possible de la simplifier. Il est cependant possible de résoudre une équation algébrique qui est en fait un ensemble de deux expressions algébriques séparées par un signe égal.

Méthode 1

Méthode 1 sur 2:
Comprendre les notions de base

1
Sachez faire la différence entre une expression algébrique et une équation algébrique. Une expression algébrique est un ensemble de nombres, de variables et d’opérateurs. Une expression algébrique ne contient pas de signe égal et ne peut pas être résolue. Une équation algébrique peut, au contraire, être résolue et est constituée de deux expressions algébriques (que l’on peut aussi appeler des membres) séparées par un signe égal. Voici quelques exemples.
- Une expression algébrique : 4x + 2
- Une équation algébrique : 4x + 2 = 100
2
Apprenez à regrouper les termes semblables entre eux. Regrouper les termes semblables entre eux signifie simplement additionner (ou soustraire) les termes de même degré. Cela veut dire que tous les termes en x² peuvent être regroupés entre eux, tous les termes en x³ peuvent être regroupés entre eux et que toutes les constantes (les nombres qui ne sont pas rattachés à des variables), comme 8 ou 5 par exemple, peuvent être combinées entre elles. Voici un exemple :
- 3x² + 5 + 4x³ - x² + 2x³ + 9 =
- 3x² - x² + 4x³ + 2x³ + 5 + 9 =
- 2x² + 6x³ + 14
3
Apprenez à factoriser un nombre. Si vous avez à résoudre une équation algébrique, ce qui veut dire qu’il y a un membre de chaque côté du signal égal, il est possible de factoriser les deux membres par un facteur commun aux deux membres. Observez les coefficients de tous les termes (les nombres devant les variables ou les constantes) et voyez si vous trouvez un facteur commun à tous ces coefficients (un nombre qui divise tous les coefficients de votre équation). Si vous pouvez faire cela (ou au contraire qu’il n’est pas possible de le faire), vous avez réussi à simplifier votre équation et vous êtes sur le bon chemin pour la résoudre. Voici un exemple :
- 3x + 15 = 9x + 30
  - Vous pouvez voir que dans cet exemple 3 divise tous les coefficients de votre équation. Factorisez vos deux membres par 3 (ce qui revient à diviser les deux membres de votre expression par 3) afin de simplifier votre équation.
- 3x/3 + 15/3 = 9x/3 + 30/3 =
- x + 5 = 3x + 10
4
Connaissez les priorités opératoires. Les priorités opératoires (que l’on peut résumer sous l’acronyme PEMDAS) donnent l’ordre dans lequel les différentes opérations mathématiques doivent être effectuées. L’ordre est le suivant : Parenthèses, Exposants, Multiplication, Division, Addition et Soustraction. Voici un exemple afin d’illustrer les priorités opératoires à respecter lors de vos calculs.
- (3 + 5)² x 10 + 4
- Tout d’abord, effectuez l’opération entre parenthèses (le P de PEMDAS)
- = (8)² x 10 + 4
- Effectuez ensuite l’opération relative à l’exposant 2 (le E de PEMDAS).
- = 64 x 10 + 4
- Effectuez ensuite la multiplication.
- = 640 + 4
- Finissez enfin par l’addition.
- = 644
5
Apprenez à isoler les variables. Si vous cherchez à résoudre une équation algébrique, votre objectif est alors de placer la variable (souvent notée x) d’un côté du signe égal et de placer les constantes de l’autre côté du signe égal. Les opérations usuelles pour isoler x d’un côté de l’équation sont la multiplication, la division, l’addition, la soustraction, le passage à la racine carrée. Il existe bien sûr encore d’autres opérations qui peuvent être utilisées, mais celles citées ici sont les plus courantes. Une fois que x est isolé, il est facile de trouver la solution à votre équation. Voici un exemple :
- 5x + 15 = 65 =
- 5x/5 + 15/5 = 65/5 =
- x + 3 = 13 =
- x = 10
Publicité

Méthode 2

Méthode 2 sur 2:
Résoudre une équation algébrique

1
Résoudre une simple équation algébrique linéaire. Une expression algébrique linéaire ne contient que des constantes et des termes du premier degré (pas d’exposant ou quoi que ce soit de ce genre). Pour résoudre ce type d’équation, il vous suffit d’utiliser des additions, soustractions, multiplications ou divisions afin d’isoler la variable (souvent notée x) puis trouver la solution de votre équation. Voici un exemple :
- 4x + 16 = 25 -3x =
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16 =
- 7x = 9
- 7x/7 = 9/7 =
- x = 9/7
2
Résoudre une équation algébrique contenant un terme du second ordre. Si votre équation contient un terme du second ordre (noté x² si x est votre variable), vous devez alors commencer par isoler la variable d’un côté du signe égal puis résoudre l’équation en « supprimant » le carré de la variable et des constantes. Voici comment faire :
- 2x² + 12 = 44
  - Commencez par soustraire 12 des deux côtés de l’équation.
- 2x² + 12 -12 = 44 -12 =
- 2x² = 32
  - Divisez ensuite chaque membre de l’équation par 2.
- 2x²/2 = 32/2 =
- x² = 16
  - Résolvez en prenant la racine carrée de chacun des membres de l’équation. En effet cela transformera le x² en x.
- √x² = √16 =
- inscrivez sur votre feuille les deux solutions : x = 4 ou -4
3
Résoudre une équation algébrique contenant des fractions. Si vous cherchez à résoudre une équation algébrique dans laquelle se trouvent des fractions, il vous faudra commencer par utiliser une règle de trois puis regrouper les termes semblables entre eux et isoler la variable. Voici comment faire :
- (x + 3)/6 = 2/3
  - Tout d’abord, commencez par utiliser la règle de trois afin de faire disparaitre les fractions. Vous devez donc multiplier chaque membre par le dénominateur de la fraction de l’autre membre.
- (x + 3) x 3 = 2 x 6 =
- 3x + 9 = 12
  - Regroupez maintenant les termes semblables. Regroupez les constantes, 9 et 12, en soustrayant 9 de chaque côté de l’équation.
- 3x + 9 - 9 = 12 - 9 =
- 3x = 3
  - Isolez la variable, x, en divisant les deux côtés de l’équation par 3, et voilà, vous avez votre solution.
- 3x/3 = 3/3 =
- x = 3
4
Résoudre une équation algébrique contenant des radicaux. Si vous devez résoudre ce type d’équations, il vous faudra alors trouver un moyen d’élever les deux membres de l’équation au carré afin de faire disparaitre les radicaux puis résoudre votre équation normalement. Voici un exemple :
- √(2x+9) - 5 = 0
  - Déplacez d’abord tout ce qui ne se trouve pas sous le radical dans l’autre membre de l’équation.
- √(2x+9) = 5
- élevez ensuite chaque membre au carré afin de supprimer les radicaux :
- (√(2x+9))² = 5² =
- 2x + 9 = 25
  - Résolvez maintenant l’équation comme une équation normale, en regroupant les constantes entre elles et en isolant la variable.
- 2x = 25 - 9 =
- 2x = 16
- x = 8
5
Résoudre une équation algébrique contenant des valeurs absolues. La valeur absolue d’un nombre représente sa valeur numérique sans prendre en compte son signe (positif ou négatif) ; la valeur absolue est donc toujours positive. Par exemple, la valeur absolue de -3 (que l’on écrit|-3|), est simplement 3. Pour résoudre ce type d’équation, il faut d’abord passer la valeur absolue d’un côté de l’équation puis résoudre deux fois l’équation, une fois lorsque ce qui se trouve dans la valeur absolue est positif et une fois lorsque ce qui se trouve dans la valeur absolue est négatif. Voici comment faire.
- Voici comment résoudre une équation contenant une valeur absolue en commençant par isoler la valeur absolue puis la supprimer et résoudre comme nous l’avons expliqué :
  - |4x +2|- 6 = 8 =
- |4x +2|= 8 + 6 =
- |4x +2|= 14 =
- 4x + 2 = 14 =
- 4x = 12
- x = 3
  - Maintenant, résolvez à nouveau en inversant les signes des termes de l’autre côté de l’équation (le côté où ne se trouvait pas la valeur absolue au début) :
- |4x +2|= 14 =
- 4x + 2 = -14
- 4x = -14 -2
- 4x = -16
- 4x/4 = -16/4 =
- x = -4
  - Écrivez maintenant les solutions sur votre feuille de papier : x = -4 ou 3.
Publicité

Conseils

Pour vérifier vos résultats, rendez-vous sur le site wolfram-alpha.com. Le site vous donne la (ou les) solution et vous permet aussi éventuellement de voir les étapes du calcul.
Une fois que vous avez fini, remplacez la variable par la valeur que vous avez trouvée et vérifiez que les deux membres de l’équation sont les mêmes. Si c’est le cas, félicitations ! Vous venez de résoudre une équation algébrique.