Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 4 110 fois.
Au lycée, les séries arithmétiques (nombres ayant une relation entre eux) sont une partie du programme et parmi les exercices proposés, il y a la sommation des n termes, n étant l'effectif de la série. La chose n'est faisable que si la série est composée d'entiers naturels, c'est-à-dire positifs. En fait, il existe des formules simples pour ce calcul, il suffit d'appliquer celle qui correspond au cas qui vous est soumis.
Étapes
Méthode 1
Méthode 1 sur 2:Vérifier la réalité d'une série arithmétique
-
1Identifiez la série arithmétique. Vérifiez que chaque terme de la série a une relation arithmétique (cela s'appelle une « raison ») avec le précédent. Sans cette précaution, les formules ne pourront pas être utilisées [1] .
- Prenons comme exemples deux séries : 5, 6, 7, 8, 9… et 17, 19, 21, 23, 25…
- Si vous aviez affaire à la série 5, 6, 9, 11, 14…, vous ne pourriez rien faire, car cette série n'a pas de raison.
-
2Repérez le dernier terme de la série (). Pour pouvoir utiliser la formule donnée plus loin, vous devez définir la valeur de , le dernier terme de la série.
- Cas simple : admettons que vous ayez à calculer la somme des termes composant la série allant de 1 à 100. , le dernier terme, vaut 100.
- Un entier naturel est un chiffre ou un nombre ni rationnel, ni fractionnaire, non plus que négatif.
-
3Déterminez l'effectif de la série à sommer. En fait, il y a là un tour de passepasse : l'effectif d'une série est égal au nombre augmenté d'une unité
(). C’est comme si l’on ajoutait le 0 en début de série. La série des 200 premiers entiers a un effectif de 201 termes [2] .- Si nous prenions comme exemple la série de raison 1 allant de 1 à 12 (1, 2, 3…,12), l'effectif serait de 13 (12 + 1).
-
4Soyez attentif(ve) aux bornes. S'il vous est demandé de faire une somme sans compter les bornes (premier et dernier termes de la série), l'effectif est alors de [3] .
- Si vous deviez faire la somme des 100 premiers entiers (1 à 100), 1 et 100 non compris, vous ôteriez 1 à 100, ce qui donnerait 99.
Publicité
Méthode 2
Méthode 2 sur 2:Utiliser des formules pour additionner des entiers
-
1Appliquez la formule de la somme des entiers consécutifs. Une fois correctement défini, il ne vous reste plus qu'à faire l'application numérique avec la formule suivante : , étant la somme des premiers entiers [4] .
- Reprenons l'exemple de la somme des entiers de la série de 1 à 100. Le dernier terme est et la formule se présente ainsi : .
- Avec la série des 20 premiers entiers consécutifs, vaudra 20. En ce cas, l'application numérique donne : . La réponse est donc : 210.
-
2Utilisez la formule pour la somme des seuls entiers pairs d'une série. Vous comprenez bien qu'il vous faut une formule autre pour la somme des seuls entiers pairs d'une série, les impairs étant exclus. La détermination de reste la même et la formule est légèrement modifiée : [5] .
- Reprenons la série composée des entiers de 10 à 20. vaut 20 comme cela a été vu plus haut, et la formule est la suivante :.
-
3Utilisez la formule pour la somme des seuls entiers impairs d'une série. C'est l'inverse de l'opération précédente : seuls comptent les entiers impairs d'une série, les pairs étant exclus. La détermination de reste la même et la formule est légèrement modifiée : [6] .
- Il vous est demandé de faire la somme des entiers impairs de la série allant de 1 à 9. valant 9, vaut 10. La formule de calcul des impairs se présente ainsi : .
-
4Utilisez les bonnes formules. En fonction de la somme qui vous est demandée, vous devez toujours déterminer en premier qu'il faudra multiplier par lui-même, augmenté ou diminué d'une certaine quantité (1 ou 2), le résultat trouvé doit être ensuite divisé par 2 ou 4 [7] .
- La somme des premiers termes de la série de 1 à 100 se calcule ainsi :
, soit , ce qui donne un total de 5 050. - La somme des seuls termes pairs de la série allant de 1 à 20 se calcule ainsi :
, soit , ce qui donne une somme de 110.
Publicité - La somme des premiers termes de la série de 1 à 100 se calcule ainsi :
Références
- ↑ https://www.mathsisfun.com/algebra/sequences-sums-arithmetic.html
- ↑ https://www.mathsisfun.com/algebra/sequences-sums-arithmetic.html
- ↑ https://gmatclub.com/forum/can-someone-tell-me-the-formula-of-consecutive-sum-85332.html
- ↑ https://cseweb.ucsd.edu/groups/tatami/kumo/exs/sum/
- ↑ https://gmatclub.com/forum/can-someone-tell-me-the-formula-of-consecutive-sum-85332.html
- ↑ https://gmatclub.com/forum/can-someone-tell-me-the-formula-of-consecutive-sum-85332.html
- ↑ https://gmatclub.com/forum/can-someone-tell-me-the-formula-of-consecutive-sum-85332.html







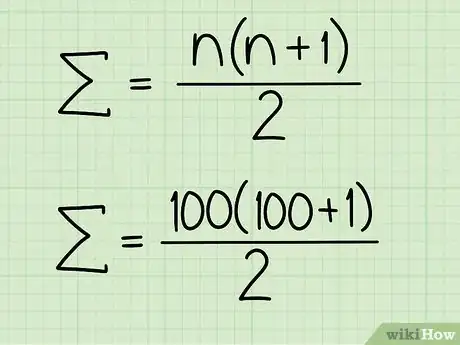





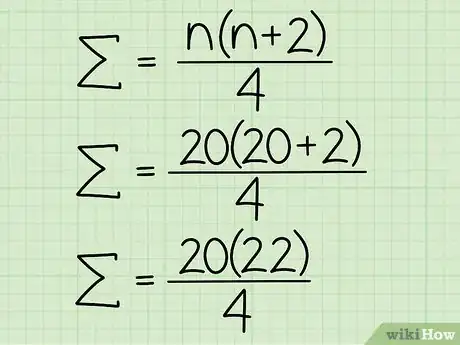


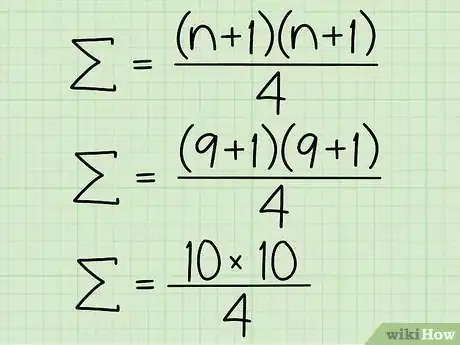


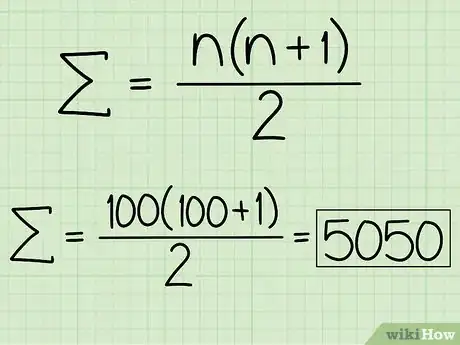























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 4 110 fois.