Comment tracer une droite parallèle à une autre et passant par un point donné

Les lignes parallèles sont des lignes qui sont toujours espacées de la même distance et qui ne se croiseraient jamais, même si elles se prolongeaient à l’infini ^{[1]
X
Source de recherche}. Parfois, il est possible que l’on vous donne une droite et que vous deviez en tracer une autre qui lui est parallèle et passe par un point précis. Vous aurez peut-être envie de simplement prendre une règle et de tracer un trait qui vous semble parallèle au premier, mais il ne risque pas d’être parfaitement parallèle. Utilisez des techniques de géométrie et un compas pour trouver d’autres points qui vous permettront de vous assurer que les deux droites sont parfaitement parallèles.

Méthode 1

Méthode 1 sur 3:
Utiliser des traits perpendiculaires

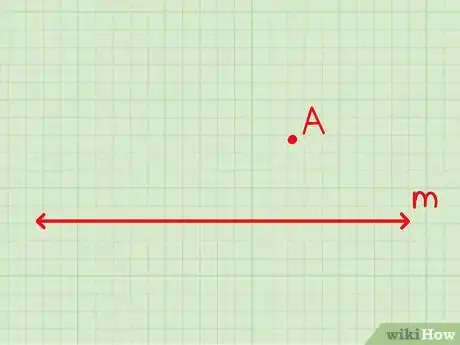
1
Trouvez les données de base. Repérez la droite dont vous disposez déjà et le point par lequel vous devez faire passer la deuxième ligne. Le point ne se trouvera pas sur la première droite et pourra se situer au-dessus ou au-dessous. Appelez la droite $m$ et le point $A$ .
2
Coupez la ligne. Tracez un arc de cercle qui coupe la droite $m$ en deux points différents. Placez la pointe de votre compas sur le point $A$ et ouvrez l’outil suffisamment pour qu’il dépasse la droite. Tracez un arc de cercle qui coupe $m$ en deux points, que vous appellerez $B$ et $C$ .
3
Tracez un petit arc de cercle. Tracez-le en face du point $A$ $A$ . Ouvrez le compas un peu plus. Posez sa pointe sur le point $B$ $B$ et tracez un arc de cercle en face du point $A$ $A$ , de l’autre côté de la droite $m$ $m$ .
- Si $A$ se trouve au-dessus de la droite, tracez l’arc de cercle au-dessous. Si $A$ se trouve au-dessous, tracez l’arc au-dessus.
- Il n’a pas besoin d’être très long du moment qu’il passe directement en face de $A$ .
4
Tracez un autre petit arc. Tracez-le de manière à ce qu’il coupe le précédent. Gardez le même écartement du compas et posez sa pointe sur le point $C$ . Tracez un arc de cercle qui coupe celui que vous avez tracé à l’étape précédente. Appelez le point d’intersection $D$ .
5
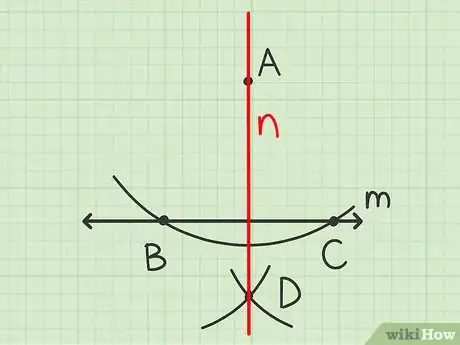
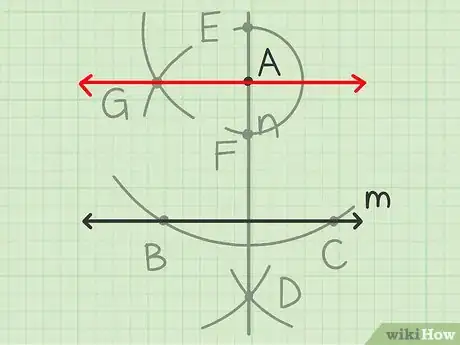
Reliez $A$ à $D$ . Tracez une ligne passant par les points $A$ $A$ et $D$ $D$ et appelez-la $n$ $n$ . Elle est perpendiculaire à $m$ $m$ et passe par $A$ $A$ et $D$ $D$ ^{[2]
X
Source de recherche}.
- Lorsqu’une ligne est perpendiculaire à une autre, cela signifie qu’elle la coupe à un angle de 90°.
6
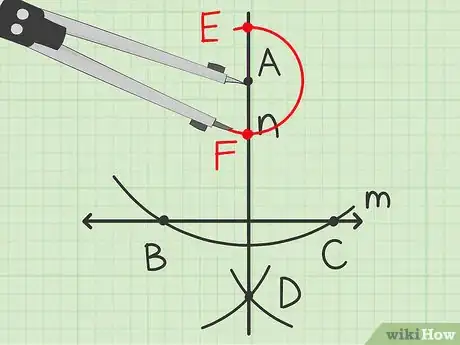
Coupez $n$ en deux points. Posez la pointe du compas sur $A$ et tracez un arc de cercle qui coupe $n$ en deux points, que vous appellerez $E$ et $F$ .
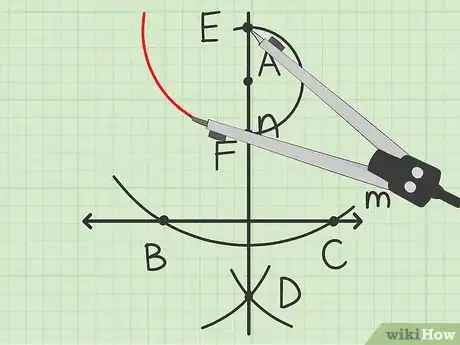
7
Tracez un arc en face de $A$ . Ouvrez légèrement plus le compas et posez sa pointe sur le point $E$ . Tracez un petit arc de cercle qui passe en face de $A$ (sur un axe invisible perpendiculaire à $n$ ).
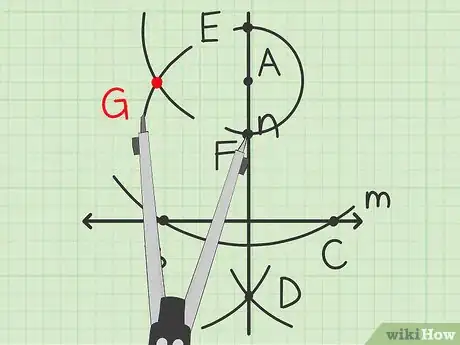
8
Coupez l’arc de cercle. Tracez un petit arc de cercle qui coupe le précédent. Gardez le même écartement du compas et posez sa pointe sur le point $F$ . Tracez un arc de cercle qui croise le précédent en face de $A$ , en un point que vous appellerez $G$ .
9
Reliez $A$ et $G$ . Tracez un trait passant par les points $A$ et $G$ . Cette ligne est perpendiculaire à $n$ ^{[3]
X
Source de recherche}, ce qui signifie que vous avez une droite parallèle à $m$ qui passe par le point donné $A$ .

Publicité

Méthode 2

Méthode 2 sur 3:
Tracer un losange

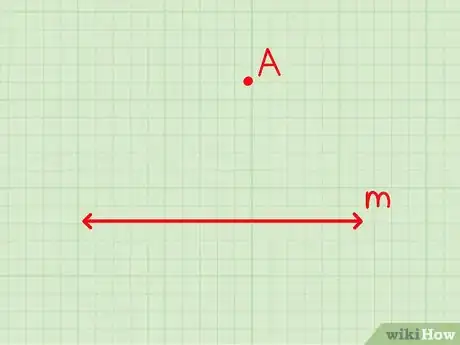
1
Trouvez les données de base. Repérez la droite dont vous disposez déjà et le point par lequel vous devez faire passer la deuxième ligne. Le point ne se trouvera pas sur la première droite et pourra se situer au-dessus ou au-dessous. Considérez-le comme un sommet du losange. Étant donné que les côtés opposés des losanges sont parallèles, vous pouvez en tracer un pour obtenir des lignes parallèles ^{[4]
X
Source de recherche}.
- Si la droite et le point donné n’ont pas de nom, vous pouvez les nommer pour pouvoir vous y retrouver facilement.
- Par exemple, vous pouvez appeler la droite $m$ et le point $A$ .
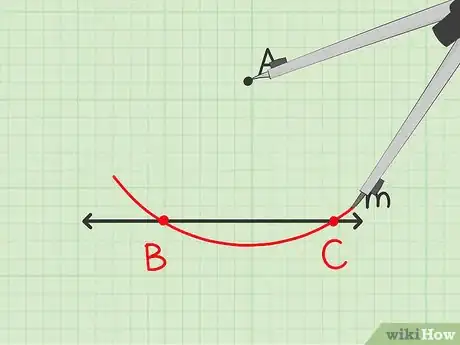
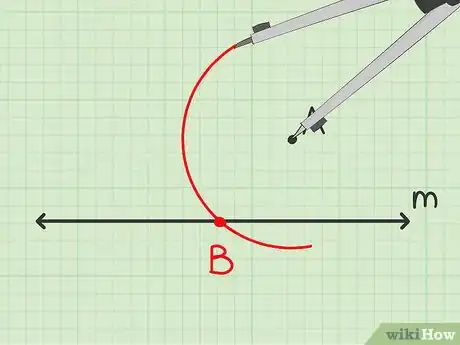
2
Trouvez le deuxième sommet du losange. Posez la pointe du compas sur le point $A$ $A$ et tracez un arc de cercle qui coupe la droite $m$ $m$ en un point quelconque.
- L’écartement du compas n’a pas d’importance du moment qu’il est suffisant pour couper $m$ .
- L’arc de cercle doit croiser la droite $m$ et se prolonger suffisamment pour passer en face du point $A$ sur une ligne imaginaire parallèle à $m$ .
- Appelez le point d’intersection $B$ .
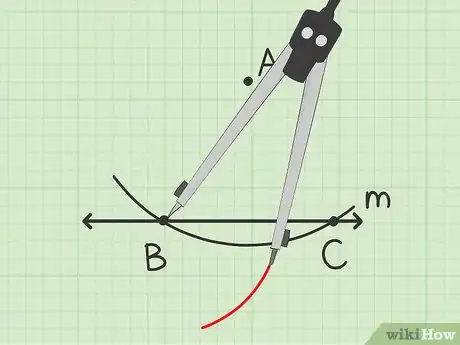
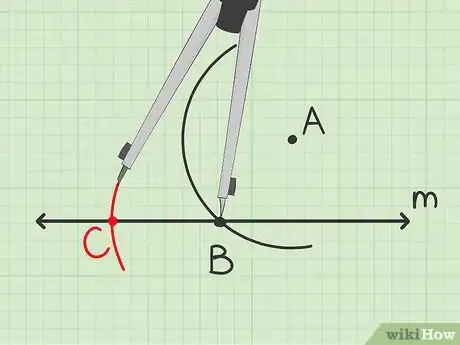
3
Trouvez le troisième sommet du losange. Gardez le même écartement du compas que pour l’étape précédente et posez sa pointe sur le point $B$ $B$ . Tracez un arc de cercle qui coupe la droite $m$ $m$ en un nouveau point.
- L’arc de cercle a seulement besoin d’être suffisamment long pour couper $m$ .
- Appelez ce nouveau point d’intersection $C$ .
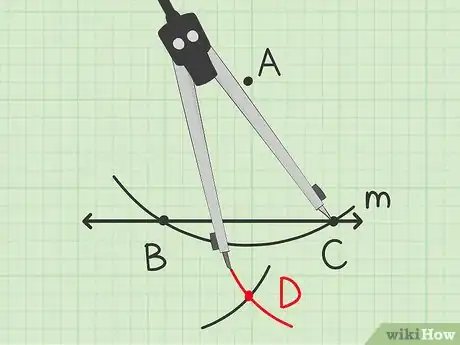
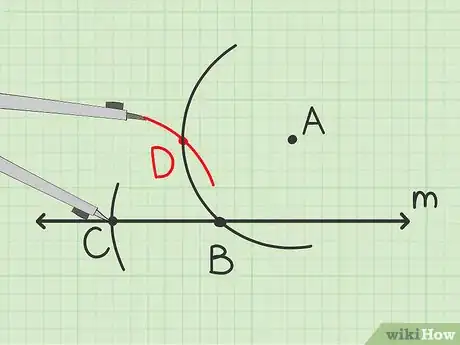
4
Trouvez le dernier sommet du losange. Gardez toujours le même écartement du compas et posez sa pointe sur le point $C$ $C$ . Tracez un arc de cercle qui coupe le premier que vous avez tracé (celui qui passe par le point $B$ $B$ ).
- L’arc de cercle a seulement besoin d’être assez long pour couper le premier arc.
- Appelez ce point d’intersection $D$ .
5
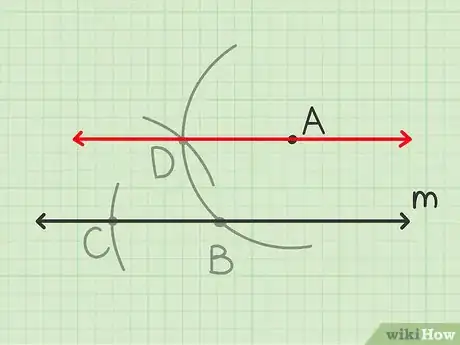
Reliez $A$ et $D$ . La ligne tracée passera par le point donné $A$ $A$ et sera parallèle à la droite $m$ $m$ , car la nouvelle droite et $m$ $m$ forment deux côtés opposés d’un losange.
- Vous avez donc une droite parallèle à la droite donnée et passant par le point donné.
Publicité

Méthode 3

Méthode 3 sur 3:
Utiliser des angles correspondants

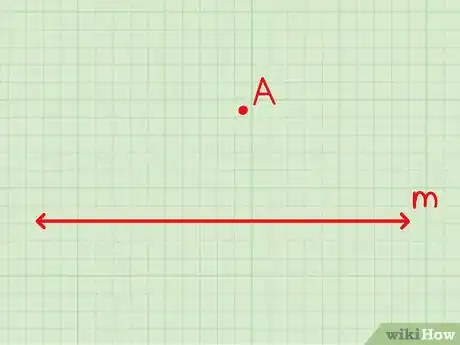
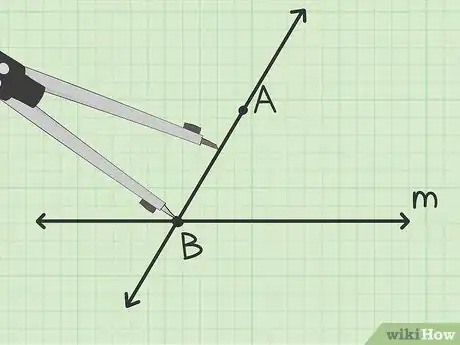
1
Trouvez les données de base. Repérez la droite dont vous disposez déjà et le point par lequel vous devez faire passer la deuxième ligne. Le point ne se trouvera pas sur la première droite et pourra se situer au-dessus ou au-dessous.
- Si la droite et le point n’ont pas de nom, vous pouvez leur en donner un pour vous y retrouver plus facilement.
- Par exemple, appelez la droite $m$ et le point $A$ .
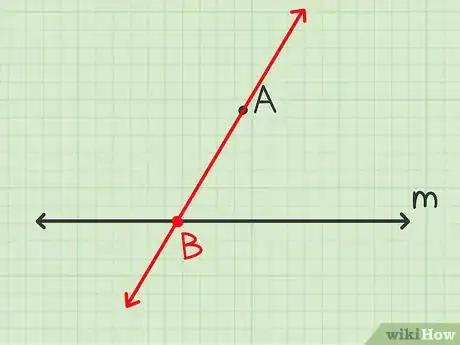
2
Tracez une droite sécante. Tracez une ligne passant par le point $A$ $A$ et un point quelconque sur $m$ $m$ . Elle vous servira à trouver les angles correspondants qui vous permettront de tracer la droite parallèle à $m$ $m$ ^{[5]
X
Source de recherche}.
- La sécante doit se prolonger bien au-delà de $A$ .
- Appelez $B$ le point d’intersection de la sécante et de $m$ . La partie de la sécante qui se trouve entre $A$ et $B$ est le segment $[AB]$ .
3
Préparez un compas. Ouvrez-le pour avoir un écartement inférieur à la moitié de la longueur du segment $[AB]$ $[AB]$ .
- L’écartement précis n’a pas d’importance du moment qu’il mesure moins de la moitié de la longueur de $[AB]$ .
- Placez sa pointe sur $A$ ou $B$ et ouvrez-le de manière à ce que son écartement corresponde à moins de la moitié de la longueur du segment.
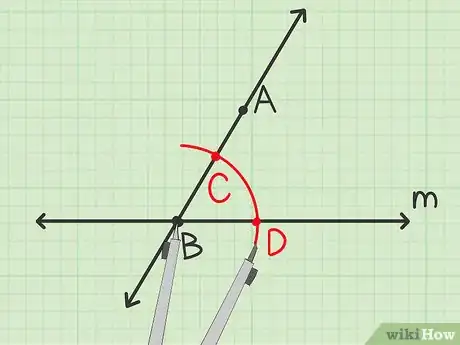
4
Tracez un premier angle. Posez la pointe du compas sur le point $B$ $B$ . Tracez un arc de cercle qui coupe la droite $m$ $m$ et sa sécante. Faites attention à ce que l’écartement du compas ne change pas.
- Posez la pointe du compas sur le point $B$ et tracez un arc de cercle qui coupe le segment $[AB]$ en un point que vous appellerez $C$ et la droite $m$ en un point que vous appellerez $D$ . Vous obtiendrez l’angle $CBD$ .
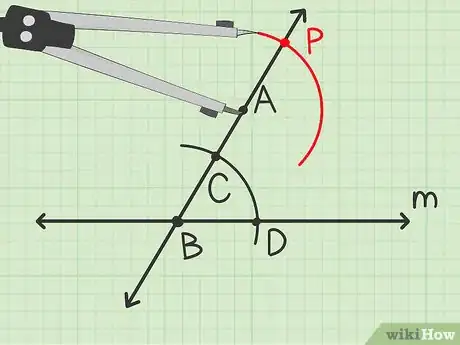
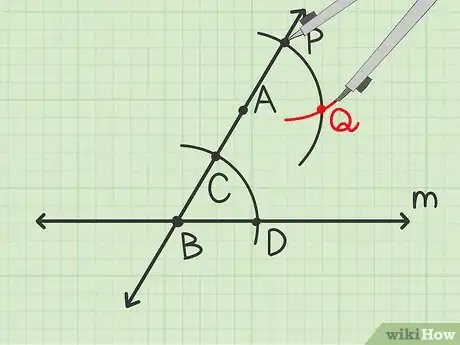
5
Tracez un arc de cercle. Gardez le même écartement du compas et posez sa pointe sur le point donné $A$ $A$ . Tracez un arc de cercle qui coupe la droite sécante $(AB)$ $(AB)$ au-dessus de $A$ $A$ et descend à un niveau juste au-dessous de celui de $A$ $A$ .
- L’arc de cercle coupe la droite $(AB)$ au-dessus de $A$ en un point que vous appellerez $P$ .
6
Changez l’écartement du compas. Réglez-le de façon à ce qu’il corresponde à la distance entre les points $C$ $C$ et $D$ $D$ .
- Posez la pointe du compas sur $C$ et ouvrez-le de manière à placer la pointe de la mine sur $D$ afin d’obtenir le bon écartement.
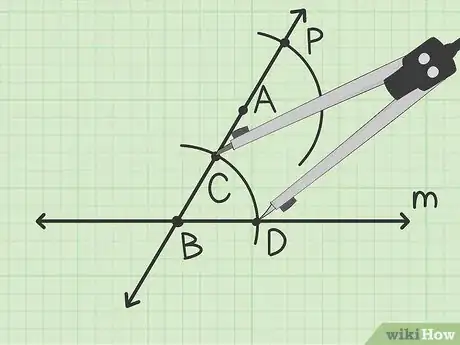
7
Tracez l’angle correspondant. Posez la pointe du compas sur le point $P$ $P$ et tracez un arc de cercle qui coupe l’arc précédent.
- Tracez un arc de cercle qui coupe celui qui passe par le point $P$ . Appelez le point d’intersection $Q$ . Vous obtiendrez l’angle $PAQ$ correspondant à l’angle $CBD$ .
8
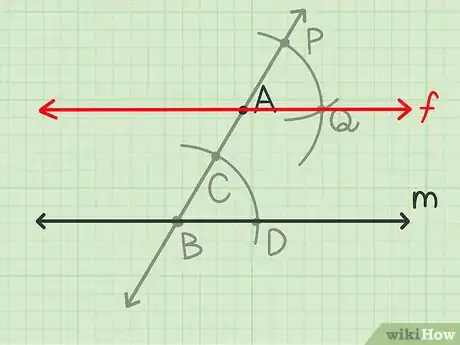
Reliez $A$ et $Q$ . Tracez une ligne passant par les points $A$ $A$ et $Q$ $Q$ . Elle sera parallèle à la droite $m$ $m$ .
- La ligne passant par $A$ et $Q$ est donc une droite parallèle à la droite donnée et passant par le point donné.
Publicité