Comment transformer une figure par rotation

Coécrit par l'équipe de wikiHow

En mathématiques, la rotation est le déplacement d'une figure par rapport à un point fixe (ou centre de rotation). Les sommets de la figure sont déplacés, mais cette dernière demeure intacte en forme, en angles et en surface ^{[1]
X
Source de recherche}. En collège, les rotations abordées sont celles autour de l'origine, point de coordonnées (0,0) dans un repère orthonormé. L'angle de rotation peut être compris entre 1° et 359°, nous verrons ici les formules des rotations de 90°, 180° et 270°.

Méthode 1

Méthode 1 sur 3:
Transformer une figure par rotation de 90°

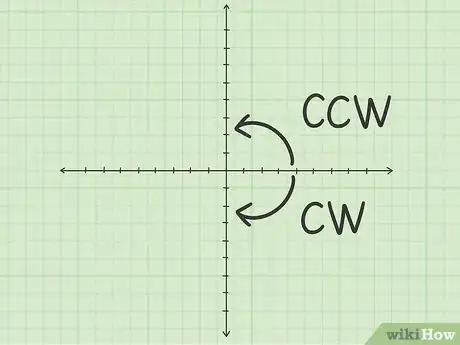
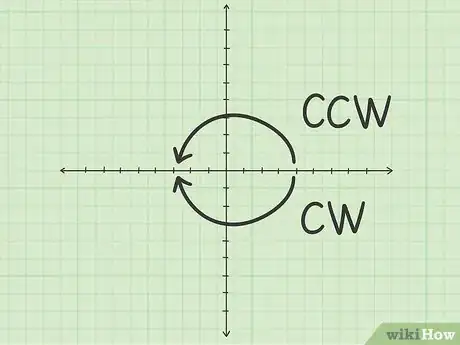
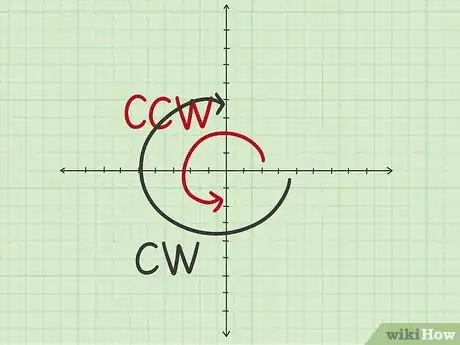
1
Comprenez le lien entre les deux types de rotation. Une figure peut tourner dans le sens direct (ou antihoraire, soit le sens contraire des aiguilles d'une montre) ou dans le sens indirect (ou horaire, soit le sens des aiguilles d'une montre). Une rotation antihoraire de 90° revient au même qu'une rotation horaire de 270° ^{[2]
X
Source de recherche}. Par convention, si le sens de la rotation n'est pas précisé, il est direct (antihoraire), c'est-à-dire vers la gauche ^{[3]
X
Source de recherche}. Le plus souvent, le sens de rotation est précisé.
- Admettons que vous ayez à résoudre l'exercice suivant : Transformer cette figure selon une rotation de 90° autour de l'origine. Le sens n'étant pas spécifié, il s'agit du sens antihoraire.
  - Cet exercice est exactement le même que celui-ci : Transformer cette figure selon une rotation de 270° dans le sens horaire autour du point origine.
  - Plus rare est la notation : Transformer cette figure selon une rotation de -270° autour de l'origine.
2
Déterminez les coordonnées des sommets de la figure de départ. Peut-être seront-elles indiquées, sinon vous les déterminerez grâce au repère. Dans le plan, un point a pour coordonnées la paire $(x,y)$ $(x,y)$ , $x$ $x$ étant son abscisse (position horizontale par rapport à 0) et $y$ $y$ son ordonnée (position verticale par rapport à 0).
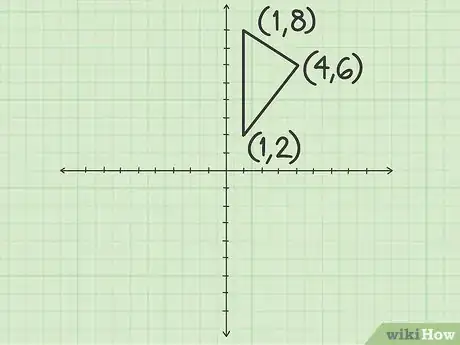
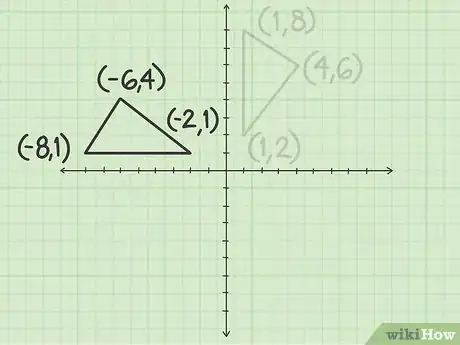
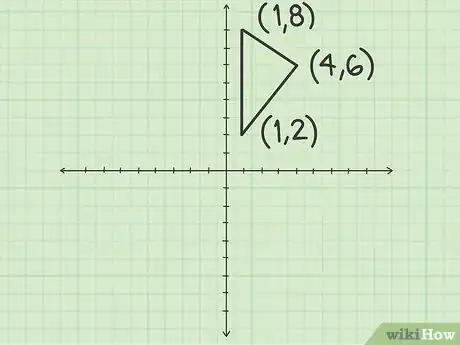
- Nous prendrons comme exemple un triangle dont les trois sommets ont pour coordonnées (4, 6), (1, 2) et (1, 8).
3
Posez la formule de la rotation à 90°. La transformation est la suivante :
$(x,y)\rightarrow (-y,x)$ ^{[4]
X
Source de recherche}. Cette rotation consiste donc à faire tourner la figure d'un quart de tour en arrière, les distances à l'origine étant conservées ^{[5]
X
Source de recherche}.
4
Faites l'application numérique. Ne mélangez pas les coordonnées de départ et celles de l'image : le point image par rotation de 90° a pour abscisse l'opposée de l'ordonnée de départ, et pour ordonnée, l'abscisse de départ.
- À la suite d'une rotation antihoraire de 90°, les images des points (4, 6), (1, 2) et (1, 8) ont pour coordonnées (-6, 4), (-2, 1) et (-8, 1).
5
Tracez la figure transformée par rotation à angle droit. Marquez les points-images, puis reliez-les à la règle. La figure obtenue est celle de départ, mais elle a subi une rotation de 90° autour de l'origine.

Publicité

Méthode 2

Méthode 2 sur 3:
Transformer une figure par rotation de 180°

1
Comprenez bien cette rotation particulière. Si l'on fait tourner une figure de 180° dans le sens horaire, cela revient au même que de la faire tourner du même angle dans le sens antihoraire : le cercle mesure 360°, le sens n'a pas besoin d'être précisé.
- Admettons que vous ayez à résoudre l'exercice suivant : Transformer cette figure selon une rotation de 180° autour de l'origine. Le sens n'étant pas spécifié, il s'agit du sens direct (antihoraire).
  - Cet exercice est exactement le même que celui-ci : Transformer cette figure selon une rotation de 180° dans le sens horaire ou antihoraire autour autour du point origine.
  - Plus rare est la notation : Transformer cette figure selon une rotation de -180° autour de l'origine.
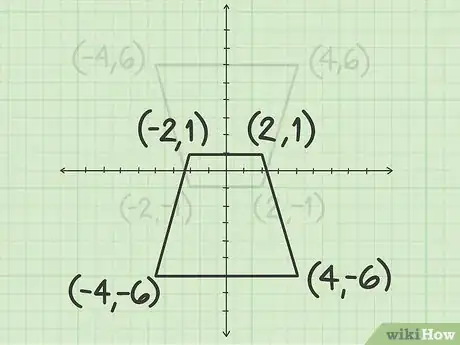
2
Déterminez les coordonnées des sommets de la figure de départ. Peut-être seront-elles indiquées, sinon vous les déterminerez grâce au repère. Les coordonnées de chacun des sommets seront soigneusement notées sous la forme
$(x,y)$ $(x,y)$ .
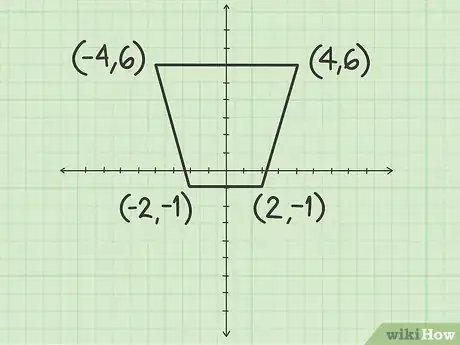
- Prenons l'exemple d'un trapèze régulier dont les sommets sont les points de coordonnées (4, 6), (-4, 6), (-2, -1) et (2, -1).
3
Posez la formule de la rotation à 180°. La transformation est la suivante :
$(x,y)\rightarrow (-x,-y)$ ^{[6]
X
Source de recherche}. Cette rotation consiste donc à faire tourner la figure d'un demi-tour en arrière, les distances à l'origine étant conservées ^{[7]
X
Source de recherche}.
4
Faites l'application numérique. Ne mélangez pas les coordonnées de départ et celles de l'image : le point image par rotation de 180° a pour abscisse l'opposée de l'abscisse de départ, et pour ordonnée, l'opposée de l'ordonnée de départ.
- À la suite d'une rotation de 180°, les images des points (4, 6), (-4, 6), (-2, -1) et
  (2, -1) ont pour coordonnées (-4, -6), (4, -6), (2, 1) et (-2, 1).
5
Tracez la figure transformée par rotation. Commencez par marquer les points-images, puis reliez-les à la règle. La figure obtenue est celle de départ, mais elle a subi une rotation de 180° autour de l'origine.

Publicité

Méthode 3

Méthode 3 sur 3:
Transformer une figure par rotation de 270°

1
Comprenez le lien entre les deux types de rotation. Une rotation directe de 270° revient au même qu'une rotation horaire de 90°. Par convention, si le sens de la rotation n'est pas précisé, c'est que celui-ci est le sens antihoraire, c'est-à-dire vers la gauche ^{[8]
X
Source de recherche}. Le plus souvent, le sens de rotation est précisé.
- Admettons que vous ayez à résoudre l'exercice suivant : Transformer cette figure selon une rotation de 270° autour de l'origine. Le sens n'étant pas spécifié, il s'agit du sens antihoraire.
  - Cet exercice est exactement le même que celui-ci : Transformer cette figure selon une rotation de 90° dans le sens horaire autour autour du point origine.
  - Plus rare est la notation : Transformer cette figure selon une rotation de -270° autour de l'origine.
2
Déterminez les coordonnées des sommets de la figure de départ. Peut-être seront-elles indiquées, sinon vous les déterminerez sur le plan, grâce au repère.
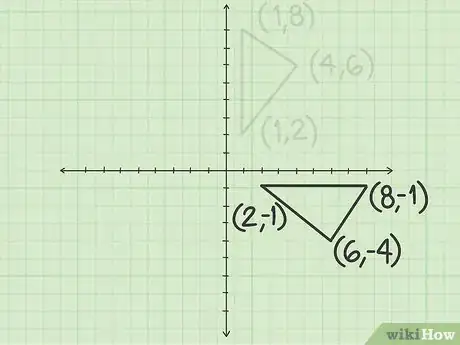
- Votre exercice concerne un triangle dont les sommets sont les points de coordonnées (4, 6), (1, 2) et (1, 8).
3
Posez la formule de la rotation à 270°. La transformation est la suivante :
$(x,y)\rightarrow (y,-x)$ ^{[9]
X
Source de recherche}. Cette rotation consiste donc à faire tourner la figure de trois quarts de tour en arrière, les distances à l'origine étant conservées ^{[10]
X
Source de recherche}.
4
Faites l'application numérique. Soyez vigilant(e) et ne mélangez pas les coordonnées : le point image par rotation de 270° a pour abscisse l'ordonnée de départ, et pour ordonnée, l'opposée de l'abscisse de départ.
- À la suite d'une rotation antihoraire de 270°, les images des points (4, 6), (1, 2) et (1, 8) ont pour coordonnées (6, -4), (2, -1) et (8, -1).
5
Tracez la figure transformée. Commencez par marquer les points-images, puis reliez-les à la règle. La figure obtenue est celle de départ, mais elle a subi une rotation de 270° autour de l'origine.

Publicité

wikiHows en relation

Publicité

Références

Plus de références

↑ http://www.virtualnerd.com/pre-algebra/geometry/transformations-symmetry/rotating-figures/rotate-90-degrees-about-origin

À propos de ce wikiHow

Coécrit par:

l'équipe de wikiHow

Rédacteurs de wikiHow

Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.

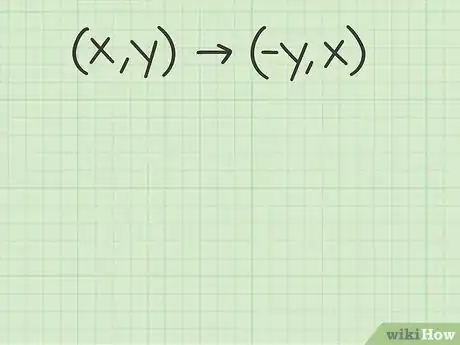
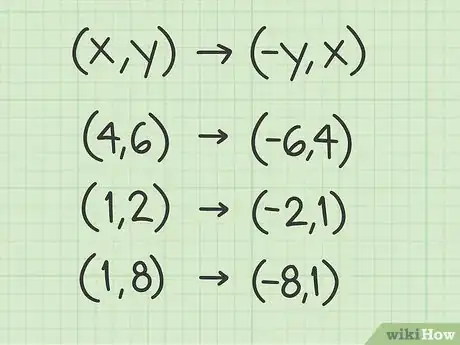
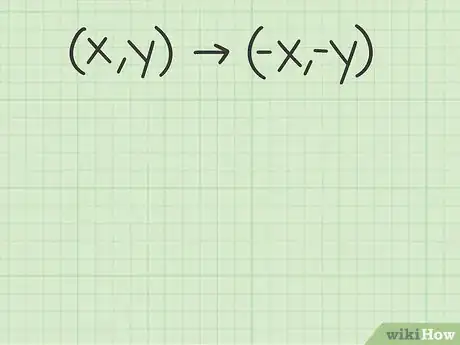
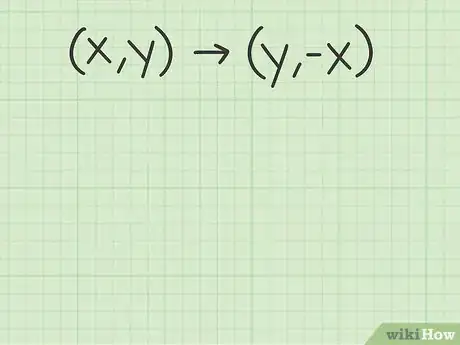
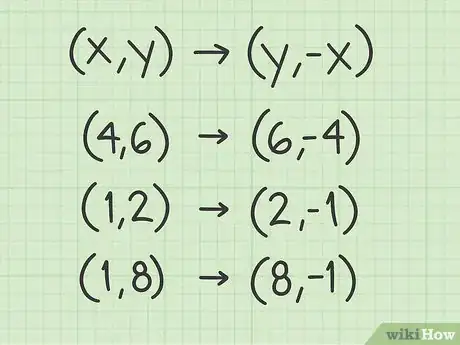
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 1 725 fois.

Catégories: Mathématiques

Publicité

Les cookies permettent d'améliorer wikiHow. En continuant la navigation, vous acceptez notre politique sur les cookies.

Articles en relation

Abonnez-vous à la newsletter gratuite de wikiHow !

Des tutoriels utiles dans votre boitier de réception chaque semaine.