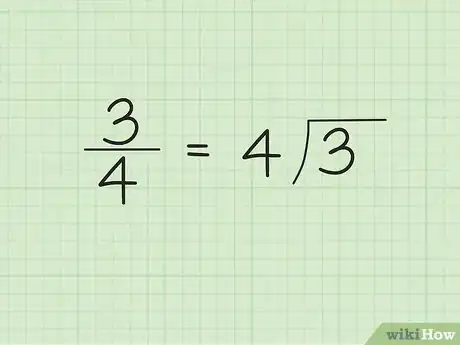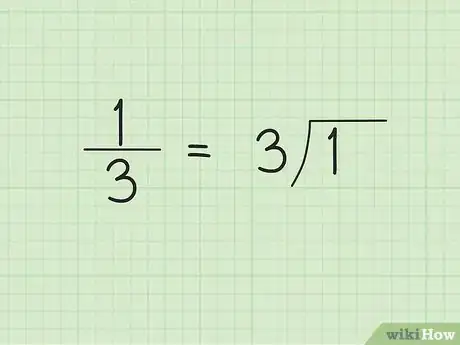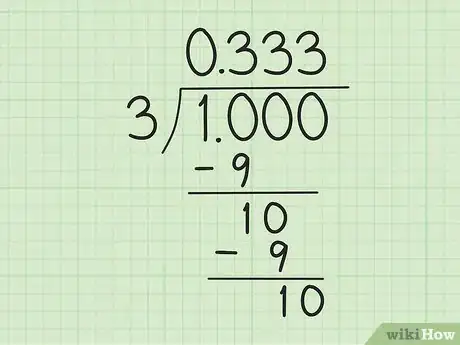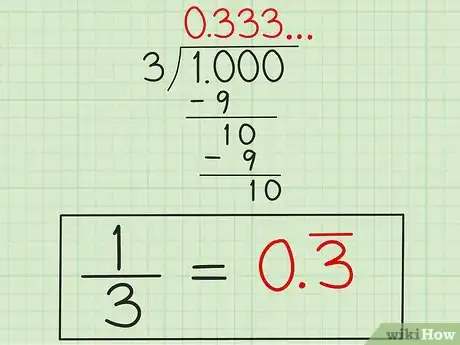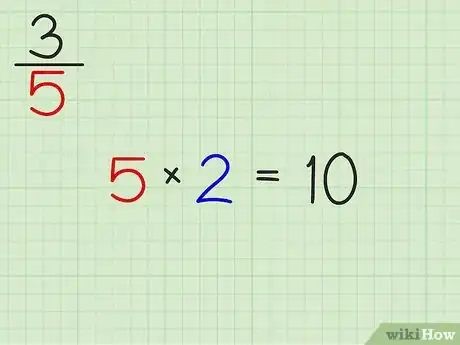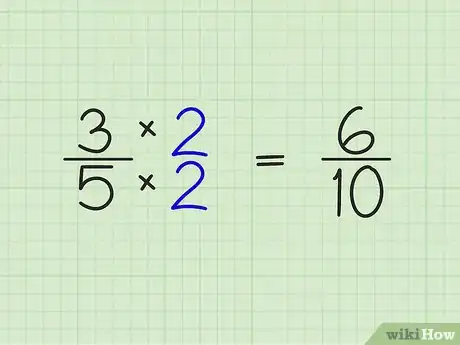Comment transformer une fraction en nombre décimal

Posez l'opération. On ne sait jamais à l'avance si on va tomber sur un résultat avec une partie décimale périodique. Prenons comme exemple la fraction irréductible 1/3 que l'on veut convertir en chiffre décimal. Placez le dénominateur 3 au-dessus du trait horizontal de division et 1 à gauche du trait vertical.

Placez un zéro avec une virgule sous la barre de division. Comme le dénominateur est plus grand que le numérateur, c'est ce qu'il faut faire d'emblée, votre nombre décimal est déjà formé.

Passez à la division proprement dite. Le chiffre 1 n'étant pas divisible par 3, on abaisse un zéro à côté du 1, d'où un 10 qui, quant à lui, est divisible par 3. Voici comment on procède :

• divisez simplement 10 par 3. Dans 10, il va 3 fois 3 (3 x 3 = 9) et il reste 1. On inscrit donc 3 en quotient, à droite du « 0, » et on inscrit 9 sous 10 de départ. On fait la soustraction pour obtenir le reste de 1,
• abaissez un nouveau zéro à côté du reste. Vous obtenez à nouveau 10, qui est à diviser par 3. Dans 10, il va 3 fois 3 (3 x 3 = 9) et il reste 1. On inscrit donc 3 en quotient, à droite du « 0,3 » et on inscrit 9 sous 10 de départ. On fait la soustraction pour obtenir un reste de 1,
• continuez la division. Ne remarquez-vous pas quelque chose de bizarre ? À chaque opération, on retombe sur la même division que précédemment et fort logiquement, sur le même reste. Vous obtenez toujours un 3 à mettre en quotient et il vous reste toujours 1.

Inscrivez votre réponse. Comme le chiffre 3 se répète à l'infini, vous n'allez pas l'écrire indéfiniment. Plusieurs écritures sont possibles : vous pouvez, par exemple, mettre un trait au-dessus de la période. Ici, ce sera un trait au-dessus du 3, ou un trait au-dessus du 33. Ainsi s'écrit 1/3 sous forme décimale, c'est-à-dire sous forme d'une valeur approchée.

• Nombreuses sont les fractions de ce genre, comme 2/9 (= 0,222, avec une période de 2), 5/6 (= 0,8333, avec une période de 3) ou 7/9 (= 0,7777, avec une période de 7). Cela arrive avec toutes les fractions dont le dénominateur est un multiple de 3 et un numérateur qui, lui, ne l'est pas.

Réduisez le dénominateur à une puissance de 10. Trouvez un nombre qui multiplié par le dénominateur donne 10, 100, 1 000 ou toute autre puissance de 10. Cette méthode permet alors d'obtenir un nombre décimal sans faire de division ni utiliser de calculatrice. En premier lieu, il convient donc de trouver un multiplicateur pour transformer le dénominateur en puissance de 10. S'il n'est pas évident, essayez de diviser 10, puis 100, 1 000… par le dénominateur. Si, à un moment donné, vous tombez sur un résultat entier, ce dernier est votre multiplicateur. Voici quelques exemples :

• prenons 3/5. Si on fait 10/5, on obtient 2, qui est un entier. Donc, si on multiplie notre dénominateur (5) par 2, on obtient 10 : 2 sera notre multiplicateur,
• prenons 3/4. Si on fait 10/4, on obtient 2,5, cela ne marche pas, car on n'a pas un entier. Par contre, si on fait 100/4, on obtient 25, on tient notre multiplicateur. Donc, si on multiplie notre dénominateur (4) par 25, on obtient 100 : 25 sera notre multiplicateur,
• prenons5/16. Si on fait 10/16, on obtient 0,625, cela ne marche pas. Pour 100/16, on obtient 6,25, cela ne marche pas non plus. Ce n'est pas mieux avec 1 000/16 (= 62,5). Par contre, avec 10 000/16, on obtient 625, qui est notre multiplicateur.

Multipliez le numérateur et le dénominateur par ce multiplicateur. C'est en effet très simple, à condition de bien multiplier le numérateur et le dénominateur par ce multiplicateur pour que la fraction soit équivalente. Reprenons nos exemples ^[1]  :

• 3/5 x 2/2 = 6/10
• 3/4 x 25/25 = 75/100
• 5/16 x 625/625 = 3 125/10 000

Trouvez la réponse finale. Mettez mentalement une virgule au numérateur (3,0 pour 3). Déplacez cette virgule vers la gauche autant fois qu'il y a de zéros dans votre dénominateur. Comptez le nombre de zéros qui compose votre dénominateur (valeur sous le trait de fraction). S'il n'y a qu'un zéro (10), déplacez la virgule du numérateur d'un rang vers la gauche. Si le dénominateur est 1 000, déplacez-la de trois rangs, etc. Vous avez alors le nombre décimal correspondant à votre fraction. Reprenons nos exemples précédents :

• 3/5 = 6/10 = 0,6
• 3/4 = 75/100 = 0,75
• 5/16 = 3 125/10 000 = 0,3125

Divisez le numérateur par le dénominateur. Rien de plus simple avec une calculatrice : divisez le numérateur, valeur du haut, par le dénominateur, valeur du bas. Si on prend la fraction 3/4, appuyez sur la touche « 3 », puis sur la touche de la division (« ÷ »), et enfin sur la touche « 4 ». Pour avoir le résultat, appuyez sur la touche « = ».